一文帶您理解正態分數變換 (Normal Score Transformation,NST)
在數據分析與建模中,許多插值和模擬方法要求輸入數據服從正態分布。而正態分數變換(Normal Score Transformation,NST)正是一種將數據轉化為標準正態分布的有效方法。通過該方法,我們可以將原始數據集轉化為一個與標準正態分布相似的數據集,從而滿足某些分析方法的需求。正態得分變換的核心步驟包括:首先對數據集進行排序并賦予秩次,然后根據秩值在標準正態分布中找到對應的分位數,最后通過這些正態分布的值構成變換后的數據集。在實際應用中,秩次的計算可以通過頻率分布或累計分布來完成,確保變換結果準確、可靠。
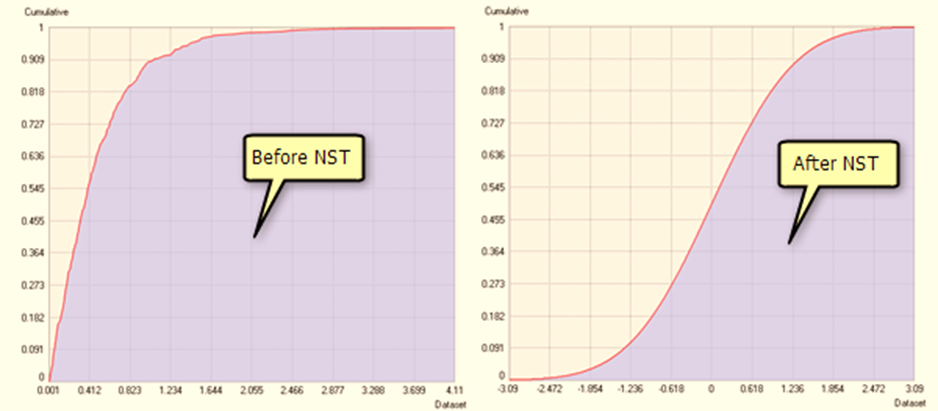
下面展示了應用正態得分變換前后,直方圖和累積分布的示例:
 圖片
圖片
 圖片
圖片
如何進行正態分數變換 (Normal Score Transformation)
對非正態分布的數據進行正態分數轉換(normal score transformation),也稱為秩正態化(rank normalizing)。具體步驟如下:
生成秩向量:首先,對原始數據 x=(x1,x2,…,xn) 進行排序,得到一個秩向量 Rx=(Rx1,Rx2,…,Rxn),其中 Rxi 表示數據點 xi 在所有觀測值中的秩次。
轉換為標準正態分布:接下來,使用秩值來計算正態分數。對于每個 xi,將秩值 Rxi 轉換為正態分布的分位數,計算公式為:
 圖片
圖片
其中,??1 是標準正態分布的逆累積分布函數(即將概率值轉換為正態分布下的對應值)。
這種方法的核心是通過秩排序將非正態數據映射到正態分布空間中,從而使數據更符合正態分布,通常用于統計分析或機器學習模型的前處理。
下面的python 代碼實現:
import numpy as np
from scipy.stats import rankdata, norm
# 假設有一組非正態分布的數據
x = [0.1, 0.2, 1.1, 1.5, 3.8, 5.4, 6.9, 6.6, 0.2, 0.2]
# 1. 計算秩向量
ranks = rankdata(x,method='average') # method {'average', 'min', 'max', 'dense', 'ordinal'}
# 2. 將秩向量轉換為正態分數
n = len(x)
x_prime = [norm.ppf(rank / (n+1)) for rank in ranks]
print("原始數據:", x)
print("秩向量:", list(ranks))
print("正態分數:",[round(num,3) for num in x_prime] ) 圖片
圖片
- rankdata(x):計算并返回數據的秩向量。秩是從 1 到 n 的整數,每個數據項對應它在排序中的位置。
- norm.ppf():計算標準正態分布的逆累積分布函數(即將概率值映射到正態分布的分位數),這里的概率是通過 Rxi /(n+1) 計算得到的。
其他修正的方式
Blom’s formula:
 圖片
圖片
Blom’s 方法引入了一個修正項,使得尾部的正態分數更加接近實際分布。
Tukey’s formula:
 圖片
圖片
Tukey 的公式類似于 Blom,但調整項略有不同。
Van der Waerden's formula
 圖片
圖片
import numpy as np
from scipy.stats import rankdata, norm
# 原始數據
x = [0.1, 0.2, 1.1, 1.5, 3.8, 5.4, 6.9, 6.6, 0.2, 0.2]
# 方法 1: 使用 average 秩和 Van der Waerden's formula
ranks_average = rankdata(x, method='average')
n = len(x)
x_prime_vdw = [norm.ppf((rank - 0.5) / n) for rank in ranks_average]
# 方法 2: Blom's formula
x_prime_blom = [norm.ppf((rank - 3/8) / (n + 1/4)) for rank in ranks_average]
# 方法 3: Tukey's formula
x_prime_tukey = [norm.ppf((rank - 1/3) / (n + 1/3)) for rank in ranks_average]
# 打印結果
print("原始數據:", x)
print("平均秩:", list(ranks_average))
print("Van der Waerden:", [round(num,3) for num in x_prime_vdw])
print("Blom:", [round(num,3) for num in x_prime_blom])
print("Tukey:", [round(num,3) for num in x_prime_tukey]) 圖片
圖片
正態分數變換與 Z-Score 標準化變換的區別
正態分數變換(NST)和 Z-Score 標準化都是數據預處理中常用的方法,但它們的目標和實現方式有顯著不同。
NST是一種非線性變換,通過將數據的秩次映射到標準正態分布的分位數,強制將非正態數據轉換為嚴格的正態分布,適用于需要數據服從正態假設的場景(如克里金插值);其優勢在于對異常值不敏感且能重塑分布形態。而Z-Score是線性變換(基于均值和標準差),僅調整數據的中心位置和尺度,不改變原始分布形狀,適用于消除量綱差異(如機器學習特征標準化),但對異常值敏感。兩者分別服務于“分布形態修正”和“數值標準化”的不同需求。
以下是兩者的主要區別:
 圖片
圖片
根據具體需求選擇合適的方法:如果需要數據嚴格服從正態分布,使用正態分數變換;如果僅需消除量綱差異,使用 Z-Score 標準化。
正態分數變換(NST)是一種將非正態分布數據轉化為接近標準正態分布的方法,主要通過對數據進行排序并根據秩值轉換為正態分布分位數。與 Z-Score 標準化不同,NST的目標是使數據符合正態分布,而 Z-Score 標準化則主要用于消除量綱差異。NST常用于統計分析和機器學習模型的前處理,以確保數據符合正態性要求。










































