大模型微調新范式:當LoRA遇見MoE
01 引言
當 LoRA 遇見 MoE,會擦出怎樣的火花?
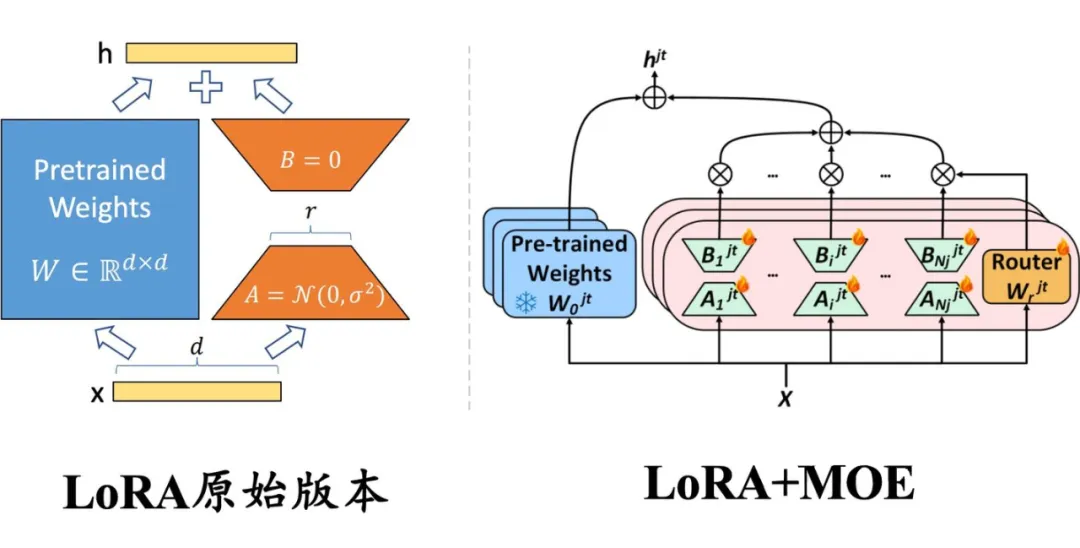
▲ 左側:原始版本的 LoRA,權重是稠密的,每個樣本都會激活所有參數;右側:與混合專家(MoE)框架結合的 LoRA,每一層插入多個并行的 LoRA 權重(即 MoE 中的多個專家模型),路由模塊(Router)輸出每個專家的激活概率,以決定激活哪些 LoRA 模塊。
由于大模型全量微調時的顯存占用過大,LoRA、Adapter、IA 這些參數高效微調(Parameter-Efficient Tuning,簡稱 PEFT)方法便成為了資源有限的機構和研究者微調大模型的標配。PEFT 方法的總體思路是凍結住大模型的主干參數,引入一小部分可訓練的參數作為適配模塊進行訓練,以節省模型微調時的顯存和參數存儲開銷。
傳統上,LoRA 這類適配模塊的參數和主干參數一樣是稠密的,每個樣本上的推理過程都需要用到所有的參數。近來,大模型研究者們為了克服稠密模型的參數效率瓶頸,開始關注以 Mistral、DeepSeek MoE 為代表的混合專家(Mixure of Experts,簡稱 MoE)模型框架。
在該框架下,模型的某個模塊(如 Transformer 的某個 FFN 層)會存在多組形狀相同的權重(稱為專家),另外有一個路由模塊(Router)接受原始輸入、輸出各專家的激活權重,最終的輸出為:
- 如果是軟路由(soft routing),輸出各專家輸出的加權求和;
- 如果是離散路由(discrete routing),即 Mistral、DeepDeek MoE 采用的稀疏混合專家(Sparse MoE)架構,則將 Top-K(K 為固定的 超參數,即每次激活的專家個數,如 1 或 2)之外的權重置零,再加權求和。
在 MoE 架構中,每個專家參數的激活程度取決于數據決定的路由權重,使得各專家的參數能各自關注其所擅長的數據類型。在離散路由的情況下,路由權重在 TopK 之外的專家甚至不用計算,在保證總參數容量的前提下極大降低了推理的計算代價。
那么,對于已經發布的稠密大模型的 PEFT 訓練,是否可以應用 MoE 的思路呢?近來,筆者關注到研究社區開始將以 LoRA 為代表的 PEFT 方法和 MoE 框架進行結合,提出了 MoV、MoLORA、LoRAMOE 和 MOLA 等新的 PEFT 方法,相比原始版本的 LORA 進一步提升了大模型微調的效率。
本文將解讀其中三篇具有代表作的工作,以下是太長不看版:
- MoV 和 MoLORA [1]:提出于 2023 年 9 月,首個結合 PEFT 和 MoE 的工作,MoV 和 MoLORA 分別是 IA 和 LORA 的 MOE 版本,采用 token 級別的軟路由(加權合并所有專家的輸出)。作者發現,對 3B 和 11B 的 T5 大模型的 SFT,MoV 僅使用不到 1% 的可訓練參數量就可以達到和全量微調相當的效果,顯著優于同等可訓練參數量設定下的 LoRA。
- LoRAMOE [2]:提出于 2023 年 12 月,在 MoLORA [1] 的基礎上,為解決微調大模型時的災難遺忘問題,將同一位置的 LoRA 專家分為兩組,分別負責保存預訓練權重中的世界知識和微調時學習的新任務,并為此目標設計了新的負載均衡 loss。
- MOLA [3]:提出于 2024 年 2 月,使用離散路由(每次只激活路由權重 top-2 的專家),并發現在每一層設置同樣的專家個數不是最優的,增加高層專家數目、降低底層專家數目,能在可訓練參數量不變的前提下,明顯提升 LLaMa-2 微調的效果。
02 MoV和MoLORA:PEFT初見MoE,故事開始
論文標題:
Pushing Mixture of Experts to the Limit: Extremely Parameter Efficient MoE for Instruction Tuning
論文鏈接:
??https://arxiv.org/abs/2309.05444??
該工作首次提出將 LoRA 類型的 PEFT 方法和 MoE 框架進行結合,實現了 MoV(IA 的 MOE)版本和 MoLORA(LORA 的 MOE)版本,發現 MoV 的性能在相等的可訓練參數量設定下優于原始的 LORA,非常接近全參數微調。回顧下IA 的適配模塊設計,即在 Transformer 的 K、V 和 FFN 的第一個全連接層的輸出,各自點乘上一個可訓練的向量 :
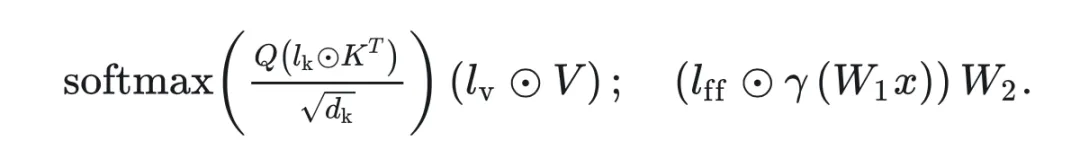
那么,MOV 就是將這些可訓練向量各自復制 份參數(n 為專家個數),并加入一個路由模塊接受 K/V/FFN 原本輸出的隱向量 、輸出各專家的激活權重,過 softmax 之后得到各專家的激活概率 ,以其為權重對各個可訓練向量求和(之后向原始版本的 IA 一樣,將求和后的向量點乘上原輸出的隱向量)。圖示如下:
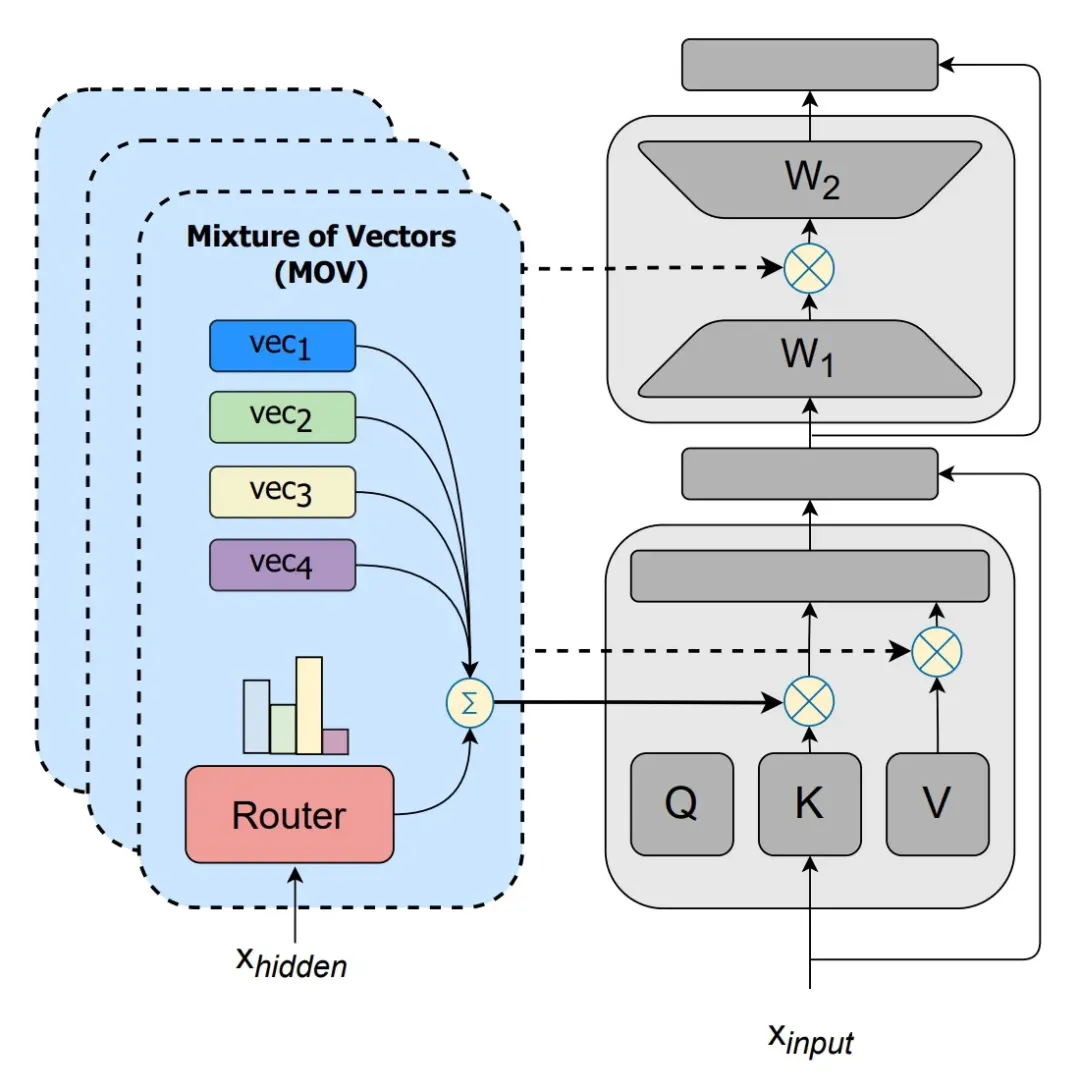
▲ MOV 方法的示意圖,引自論文[1]。
實驗部分,作者在 Public Pool of Prompts 數據集上指令微調了參數量從 770M 到 11B 的 T5 模型,在 8 個 held out 測試集上進行測試。實驗的微調方法包括全量微調、原始版本的 IA 和 LORA、MoV 和 MoLORA。
從測試結果上來看,MoV的性能明顯好于 MoLORA 和原始版本的 IA 和 LORA。例如,專家個數 的 MoV-10 只用 3B 模型 0.32% 的參數量,就能達到和全量微調相當的效果,明顯優于同等可訓練參數量的 IA 和 LORA,而使用 0.68% 可訓練參數的 MoV-30(60.61)甚至超過全量微調。
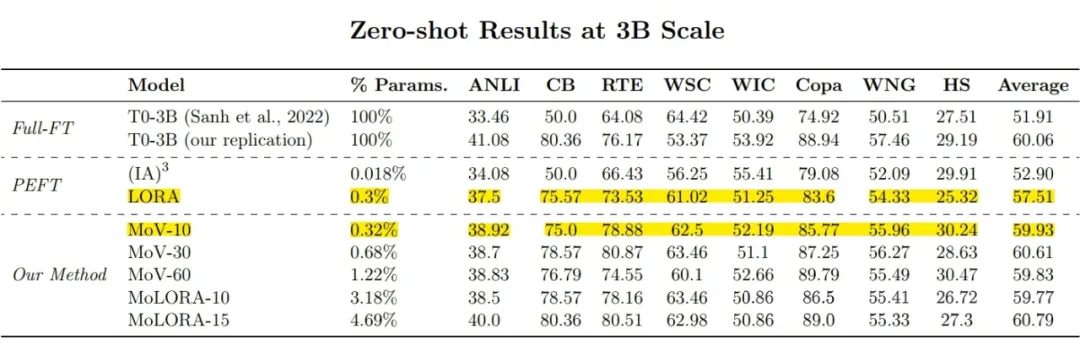
▲ 3B 模型的測試結果,只使用 0.32% 可訓練參數的MoV-10 的平均 accuracy(59.93)接近全量微調(60.06),明顯優于使用 0.3% 可訓練參數的原始版本 LORA(57.71)。使用 0.68% 可訓練參數的 MoV-30(60.61)甚至超過全量微調。
此外,作者還對專家的專門程度(speciality,即每個任務依賴少數幾個特定專家的程度)進行了分析,展示 MOV-5 微調的 770M 模型最后一層 FFN 中各專家路由概率的分布:
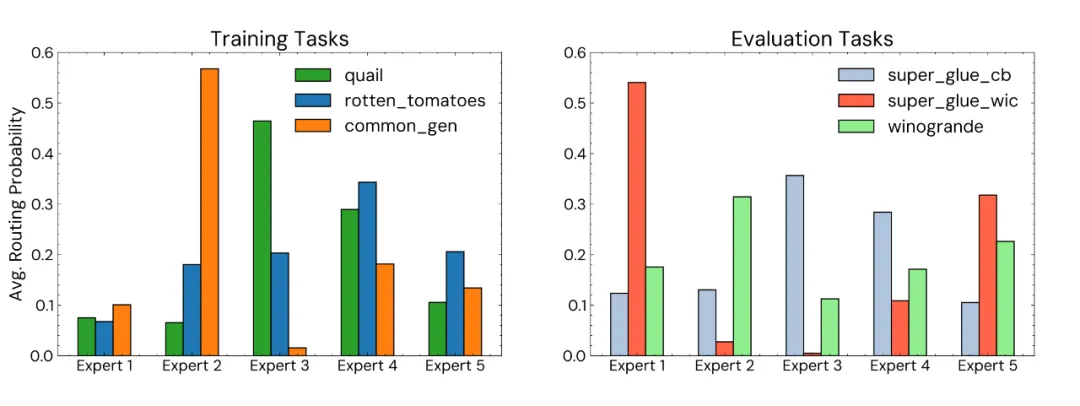
▲ 路由概率的分布,左側為模型在訓練集中見過的任務,右側為測試集中模型未見過的任務。
可以看出,無論模型是否見過任務數據,大多數任務都有 1-2 個特別側重的專家占據了大部分激活概率值,說明 MoV 這個 MoE 實現達成了專家的專門化。
03 LoRAMOE:LoRA專家分組,預訓練知識記得更牢
論文標題:
LoRAMoE: Revolutionizing Mixture of Experts for Maintaining World Knowledge in Language Model Alignment
論文鏈接:
??https://arxiv.org/abs/2312.09979??
此文為復旦大學 NLP 組的工作,研究動機是解決大模型微調過程中的災難遺忘問題。
作者發現,隨著所用數據量的增長,SFT 訓練會導致模型參數大幅度偏離預訓練參數,預訓練階段學習到的世界知識(world knowledge)逐漸被遺忘,雖然模型的指令跟隨能力增強、在常見的測試集上性能增長,但需要這些世界知識的 QA 任務性能大幅度下降:
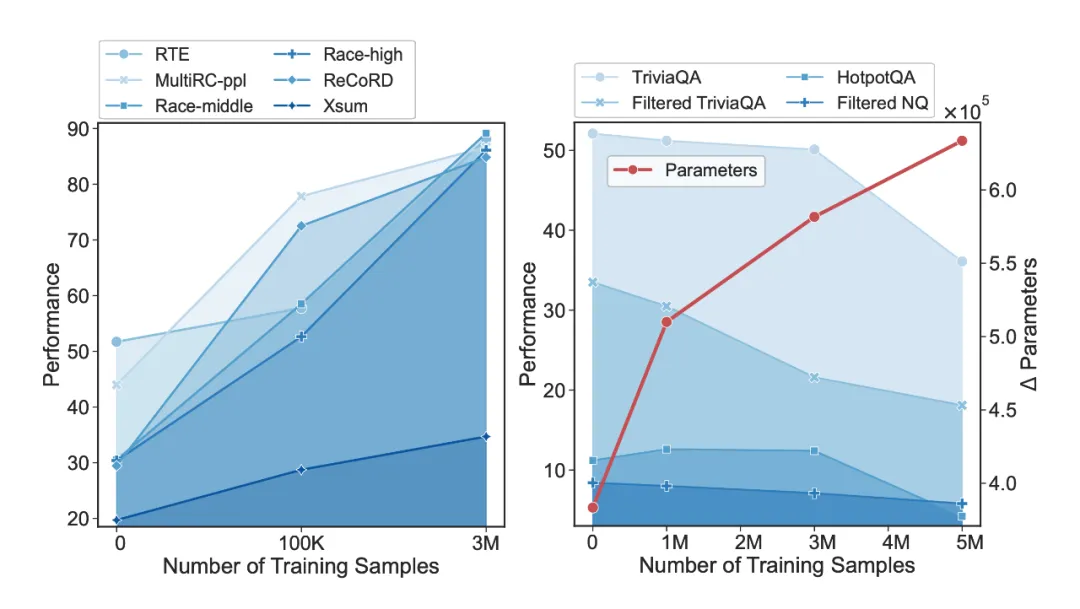
▲ 左側為不需要世界知識的常見測試集上的性能,右側為需要世界知識的 QA 測試集上的表現,橫軸為 SFT 數據量,紅線為模型參數的變化程度。
作者提出的解決方案是:
- 數據部分:加入 world knowledge 的代表性數據集 CBQA,減緩模型對世界知識的遺忘;
- 模型部分:以(1)減少模型參數變化、(2)隔離處理世界知識和新任務知識的參數為指導思想,在上一篇文章的 MoLORA 思想上設計了 LoRAMoE 方法,將 LoRA 專家們劃分為兩組,一組用于保留預訓練參數就可以處理好的(和世界知識相關的)任務,一組用于學習 SFT 過程中見到的新任務,如下圖所示:
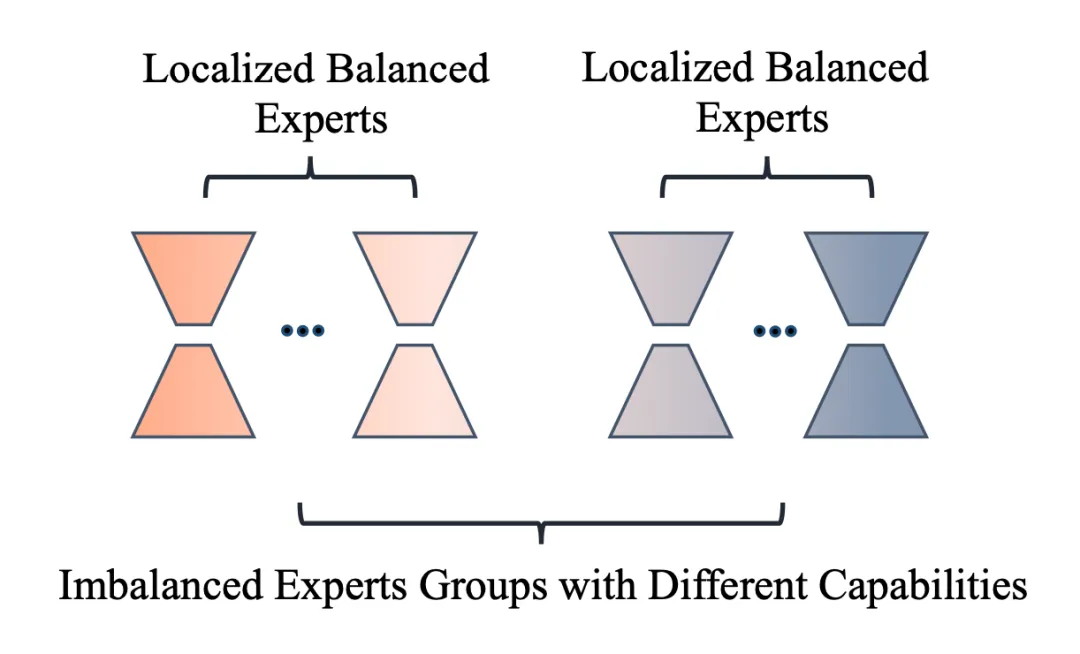
為了訓練好這樣的分組專家,讓兩組專家在組間各司其職(分別處理兩類任務)、在組內均衡負載,作者設計了一種名為 localized balancing contraint 的負載均衡約束機制。具體地,假設 為路由模塊輸出的重要性矩陣, 代表第 個專家對第 個訓練樣本的權重, 作者定義的和 形狀相同的矩陣:
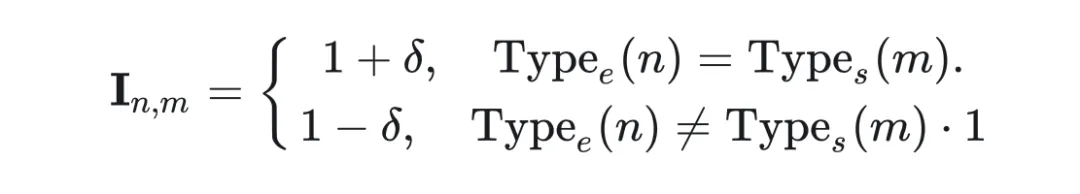
其中 為 0-1 之間的固定值(控制兩組專家不平衡程度的超參), 為第 個專家的類型(設負責保留預訓練知識的那組為 0,負責習新任務的那組為1), 為第 個樣本的類型(設代表預訓練知識的 CBQA 為 0,其他 SFT 數據為 1)。負載均衡損失 的定義為用 加權后的重要性矩陣 的方差除以均值:
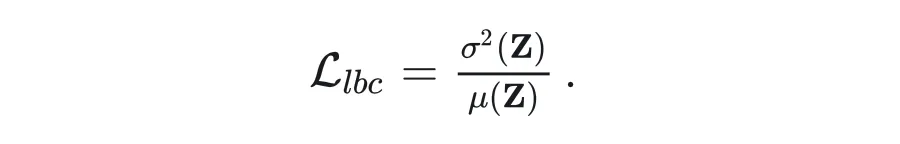
這樣設計 loss 的用意是,對任意一種訓練樣本,兩組 LoRA 專家組內的 值是相等的,優化 即降低組內路由權重的方差,使得組內負載均衡;兩組專家之間,設專家組 A 對當前類型的數據更擅長,則其 值大于另一組專家 B,訓練起始階段的 A 的激活權重就顯著大于 B,A 對這種數據得到的訓練機會更多,路由模塊在訓練過程中逐漸更傾向對這種數據選擇A組的專家。
這種“強者愈強”的極化現象是 MoE 領域的經典問題,可以參見經典的 sMoE 論文 The Sparsely-Gated Mixture-of-Experts Layer [4] 對該問題的闡述。
這樣一來,即使推理階段沒有數據類型 的信息,A 對這種數據的路由值 也會顯著大于 B 的相應值,這就實現了兩組專家各司其職的目標。
實驗部分,作者在 CBQA 和一些列下游任務數據集混合而成的 SFT 數據上微調了 LLaMA-2-7B,對比了全量 SFT、普通 LORA 和作者所提的 LoRAMoE 的性能。
結果顯示,LoRAMoE 有效克服了大模型 SFT 過程中的災難性遺忘問題,在需要世界知識的 QA 任務(下表下半部分)上性能最佳,在與 SFT 訓練數據關系更大的其他任務上平均來說基本與 SFT 訓練的模型相當:
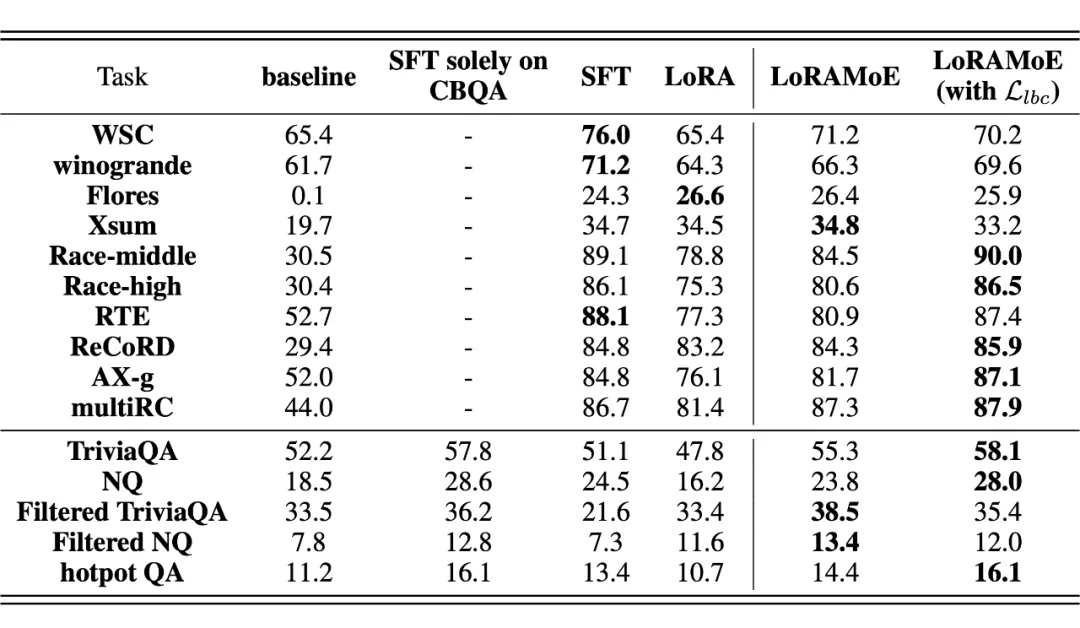
04 MOLA:統籌增效,更接近輸出端的高層需要更多專家
論文標題:
Higher Layers Need More LoRA Experts
論文鏈接:
??https://arxiv.org/abs/2402.08562???
該工作受到 MoE 領域先前工作 [5] 發現的專家個數過多容易導致性能下降的現象之啟發,提出了兩個問題:
- 現有 PEFT+MoE 的微調方法是否存在專家冗余的問題?
- 如何在不同中間層之間分配專家個數?
為了解答問題 1,作者訓練了每層專家個數均為 5 的 LoRA+MoE(基座模型為 32 層的 LLaMa-2 7B),路由機制采用 Top-2 離散路由,計算了每層 self-attention 的 Q、K、V、O 各組專家權重內兩兩之間求差的 Frobenius 范數的平均值,可視化如下:
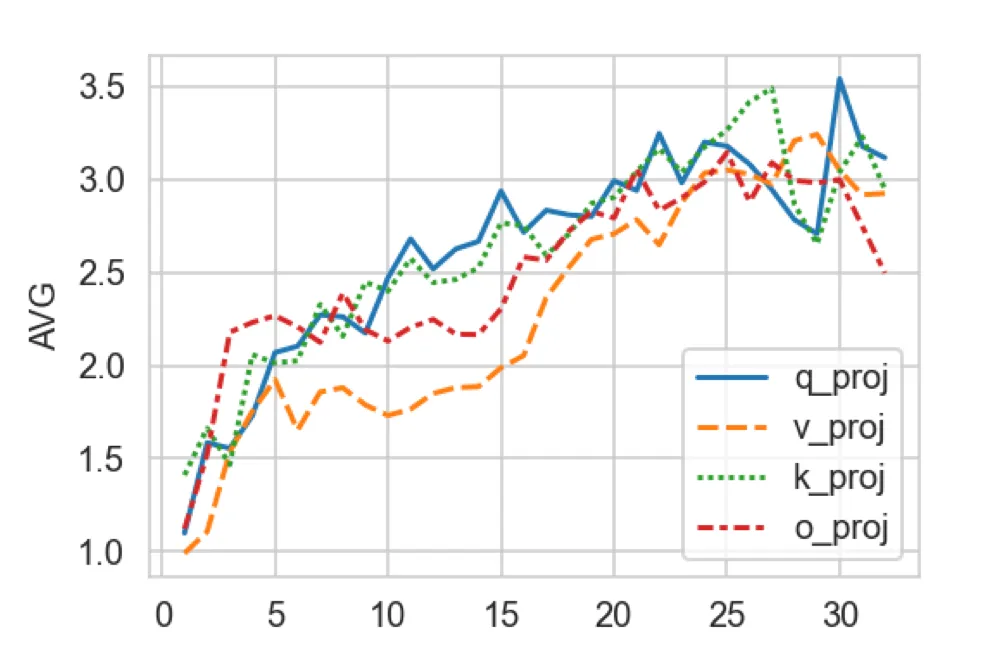
▲ 橫軸為模型層數,縱軸為專家權重之間的差異程度。
可以看出,層數越高(約接近輸出端),專家之間的差異程度越大,而低層的專家之間差異程度非常小,大模型底層的 LoRA 專家權重存在冗余。該觀察自然導出了對問題 2 答案的猜想:高層需要更多專家,在各層的專家個數之和固定的預算約束下,應該把底層的一部分專家挪到高層,用原文標題來說就是:
Higher Layers Need More Experts
為了驗證該猜想,作者提出了四個版本的專家個數劃分方式分別嚴重性能,它們統稱為 MoLA(MoE-LoRA with Layer-wise Expert Allocation),分別是:
- MoLA-△:正三角形,底層專家個數多,高層專家個數少;
- MoLA-▽:倒三角形,底層少,高層多;
- MoLA-??: 沙漏型,兩頭多、中間少;
- MoLA-□:正方形,即默認的均勻分配。
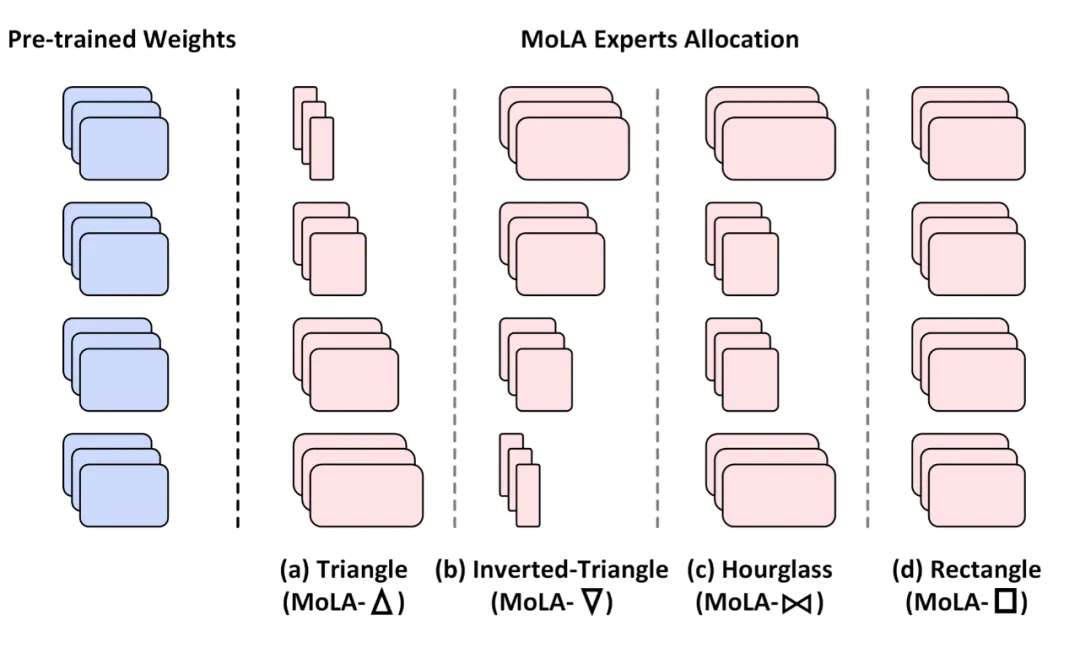
▲ 四種在不同中間層之間劃分專家個數的方式。
具體實現中,作者將 LLaMA 的 32 層從低到高分為 4 組,分別是 1-8、9-16、17-24、25 到 32 層,以上四種劃分方式總的專家個數相等,具體劃分分別為:
- MoLA-△:8-6-4-2
- MoLA-▽:2-4-6-8;
- MoLA-??: 8-2-2-8;
- MoLA-□:5-5-5-5。
路由機制為 token 級別的 Top-2 路由,訓練時加入了負載均衡損失。MoLA 的 LoRA rank=8,基線方法中 LoRA 的秩為 64(可訓練參數量略大于上述四種 MoLA,與 MOLA-□ 的 8-8-8-8 版本相同)評測數據集為 MPRC、RTE、COLA、ScienceQA、CommenseQA 和 OenBookQA,在兩種設定下訓練模型:
- 設定1:直接在各數據集的訓練集上分別微調模型;
- 設定2:先在 OpenOrac 指令跟隨數據集上進行 SFT,再在各數據集的訓練集上分別微調模型。
從以下實驗結果可以看出,在設定 1 下,MoLA-▽ 都在大多數數據集上都取得了 PEFT 類型方法的最佳性能,遠超可訓練參數量更大的原始版本 LoRA 和 LLaMA-Adapter,相當接近全量微調的結果。
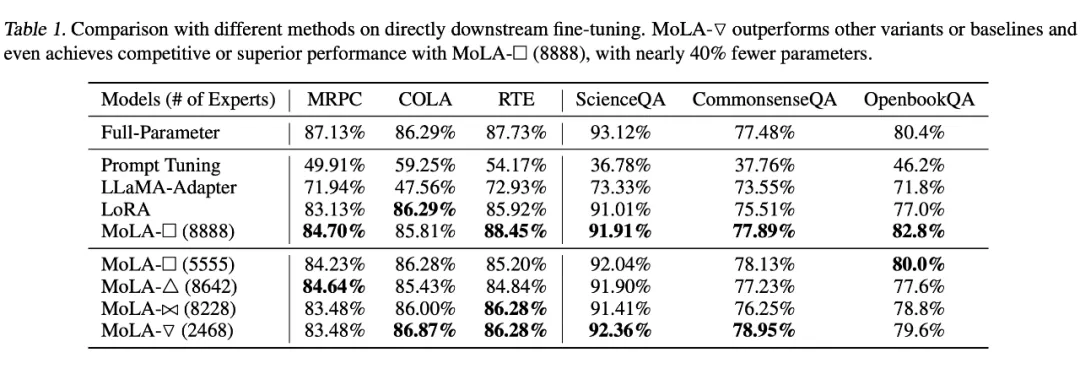
▲ 設定1下的實驗結果
在設定 2 下,也是倒三角形的專家個數分配方式 MoLA-▽ 最優,驗證了“高層需要更多專家”的猜想。
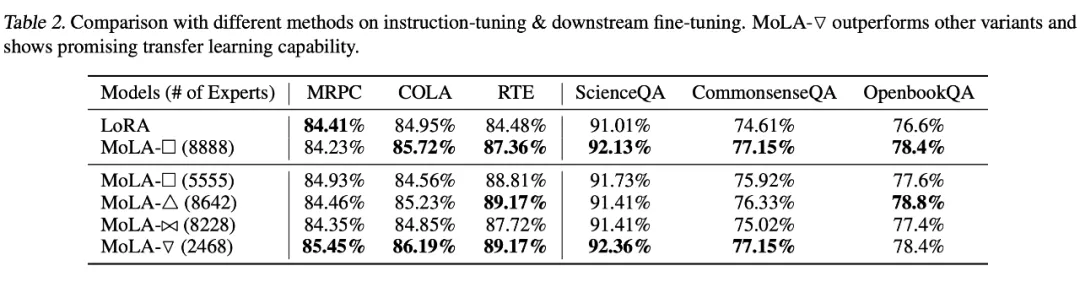
筆者點評:從直覺來看,模型的高層編碼更 high-level 的信息,也和目標任務的訓練信號更接近,和編碼基礎語言屬性的底層參數相比需要更多調整,和此文的發現相符,也和遷移學習中常見的 layer-wise 學習率設定方式(頂層設定較高學習率,底層設定較低學習率)的思想不謀而合,未來可以探索二者的結合是否能帶來進一步的提升。
本文轉自 PaperWeekly ,作者: 陳思碩

















