從原理到調參,小白也能讀懂的大模型微調LoRA,不懂線性代數也沒問題 原創
身為一名AI工程師,我過去的工作主要集中在應用層開發,對算法的理解并不深入。然而,近期我開始對算法產生了濃厚的興趣,并轉向研究模型微調。在眾多微調算法中,Lora以其普遍應用引起了我的關注,我計劃在本文中對它進行詳細介紹。將Lora僅僅視為一種算法可能并不準確,它更像是一種精妙的技巧或策略。下文將圍繞幾個核心問題,全面探討和解析Lora技術,希望這些內容能為對模型微調感興趣的你提供有用的參考和幫助。
Lora是什么
假設大模型的原始的權重矩陣w是:
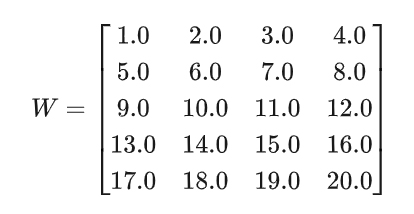
全量微調需要更新 5 * 4 = 20個參數,假設微調后的參數是:

這個可以轉化為:
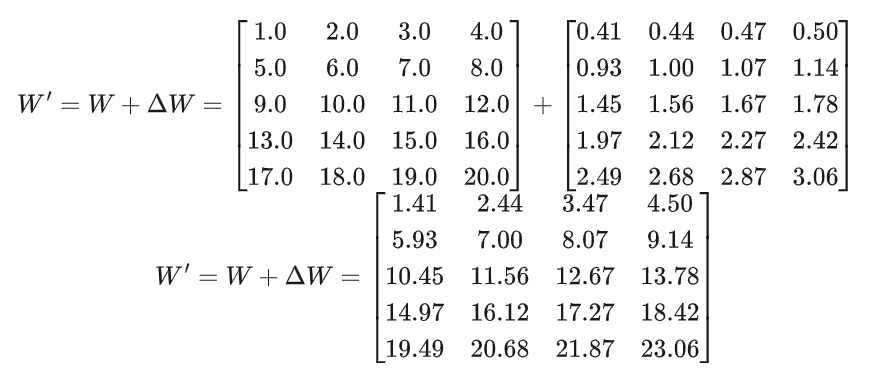
其中ΔW 可以分解為

- 矩陣 ( A ):尺寸 ( 5 * 2 ),共10個參數
- 矩陣 ( B ):尺寸 ( 2 * 4 ),共8個參數
- LoRA總參數:( 10 + 8 = 18 ) 個
也就是說通過LoRA微調,調參對象從 W 變為 A、B,使得參數量從20個減少為18個,這是簡化的例子。在實際案例中,參數量可以減少為0.01%~3%左右。
為什么需要LoRA
LoRA最早出現在2021年由微軟研究院提出的一篇論文中(《LoRA: Low-Rank Adaptation of Large Language Models》),LoRA的核心思路是:與其每次都復制整個模型,不如只調整一小部分參數,把成本降下來。它的目標是解決大模型微調中的兩大痛點:
- 資源消耗太大:大型語言模型動輒幾億甚至幾千億參數,全參數微調需要為每個新任務保存一份完整的模型副本。比如,一個10億參數的模型,假設每個參數用4字節(float32),光存儲就得4GB。多個任務下來,硬盤和顯存都吃不消。
- 訓練效率低下:全參數微調不僅占空間,還需要大量計算資源和時間。每次訓練都得更新所有參數。
LoRA的核心亮點
- 參數少
- 在GPT-3上,?
?r = 8??的LoRA參數量占全微調的0.01%-0.1%,性能卻達到全微調的95%-99%。 - 在GLUE任務(BERT),?
?r = 16??的LoRA用0.1%參數,平均得分僅比全微調低0.5-1分。 - 它只微調原始參數的1%甚至更少。
- 速度快
- 訓練和部署都比全參數微調省時省力。
- 模塊化
- 訓練好的LoRA“插件”可以隨時加載或卸載,不影響原始模型,特別適合多任務場景。
模塊化設計的優點
- 避免災難性遺忘
直接修改???W??? 可能導致模型在新任務上表現良好,但在原始任務上性能下降(即“災難性遺忘”)。LoRA通過凍結核心??W??,保留了原始模型的能力。 - 存儲高效
一個大模型可以搭配多個LoRA模塊,每個模塊只占用MB級空間,相比全模型微調動輒幾GB,節省顯著。 - 快速切換任務
任務切換只需加載不同LoRA文件,幾秒鐘搞定,不用重新訓練。 - 兼容性強
原始模型完全不動,多個團隊可以共享同一個基礎模型,只開發自己的LoRA模塊。
為什么可以對增量權重 ΔW 低秩分解?
低秩分解的核心思想是:矩陣里的信息往往不是均勻分布的,很多維度是冗余的,只需要抓住"主要方向"就夠了。
1. 什么是矩陣的秩(Rank)?
在線性代數中,一個矩陣的秩(rank)是它的線性獨立行或列的數量。如果一個矩陣是"低秩"的,意味著它的信息可以用少量獨立方向表達,而不是需要完整的維度。
比如下述矩陣,第5行 ??[1, 2, 0, 3, 0]??? 是第1行 ??[1, 0, 0, 2, 0]??? 和第2行 ??[0, 2, 0, 1, 0]?? 的線性組合(第5行=第1行+第2行),第5行沒有提供更多的信息,理論上這個矩陣有前4行就能提供所有信息了,因此矩陣的行秩為4(列秩也為4,第5列全為0,沒有信息增量)。
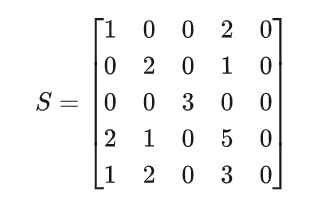
2. 低秩分解的原理
奇異值分解(SVD)可以把任意矩陣分解成三個矩陣的乘積。對于一個形狀 ( d * k ) 的矩陣 ( W ),SVD可以寫成:

- ( U ) 是 ( d * d ) 的正交矩陣
- (Σ ) 是 ( d * k ) 的對角矩陣(奇異值按降序排列)
- ( V^T ) 是 ( k * k ) 的正交矩陣(( V ) 的轉置)
其中 ( r ) 是矩陣的秩(非零奇異值的數量)。通過保留前 ( r ) 個最大的奇異值(低秩近似),可以用更少的參數近似原矩陣 ( W )。
任意矩陣(無論是實數還是復數、方陣還是非方陣、滿秩還是不滿秩)都可以通過奇異值分解(SVD)精確拆分為三個特定矩陣的乘積
舉個例子,針對上述矩陣 ( S ) 的SVD分解(計算過程略):

如果只保留前三個奇異值(7.03, 3, 2.15),重構后的矩陣 ( S' ) 與原矩陣 ( S ) 幾乎一致(三個矩陣分別取前三列,前三行&前三列,前三行):
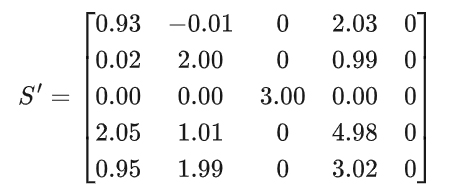
結果對比原始矩陣和重構矩陣,直觀上來看,基本保持一致,這就是說:如果只保留最大的幾個奇異值,就能用更少的參數近似表示w。
3. 為什么可以對增量權重 ΔW 低秩分解?
研究發現:
- 信息集中性:微調后的權重變化 ( ΔW) 的奇異值分布中,前10-20個奇異值占據了90%以上的信息(LoRA論文在GPT-3上的實驗結論)。
- 結構化特性:(ΔW ) 的變化不是隨機的,而是集中在少數"任務相關方向"上(例如讓模型學習法律術語只需調整少量語義方向)。
- 高效近似:直接用低秩矩陣 ( A * B ) 構造 (ΔW ),無需完整SVD計算,參數量從 ( d * k ) 降至 ( (d + k) * r )。
直觀理解: 微調類似于讓一個已學會"說話"的模型掌握某種"口音"。這種調整只需修改少數關鍵維度(如詞匯選擇),而非全部語言規則,因此低秩足夠。
舉個例子:
對一個 ( 512 * 512 ) 的權重矩陣(262,144參數):
- 全微調:更新全部262,144個參數。
- LoRA(( r=8 )):僅需 ( 512 * 8 + 8 * 512 = 8,192 ) 個參數,即可捕捉主要變化。
4. 對原始權重 ( W ) 可以低秩分解嗎?
不行。預訓練模型的權重 ( W ) 通常接近滿秩(奇異值分布平滑),低秩分解會丟失關鍵信息。而 ( ΔW ) 的秩天然較低,適合分解。
LoRA是如何更新參數的
本質上,LoRA仍然使用反向傳播算法進行參數更新,但僅針對新增的低秩矩陣 ( A ) 和 ( B ),而保持原始權重 ( W ) 凍結。
參數更新過程
(1)初始化
- ( W ) 使用預訓練模型的權重,梯度計算被禁用(不更新)。
- ( A ) 用小的隨機高斯分布初始化
- ( B ) 初始化為全零矩陣,確保訓練開始時 ( ΔW = 0 ),避免干擾原始模型。
(2)前向傳播
- 輸入數據 ( X ) 通過調整后的權重計算輸出
- 根據任務目標 計算損失函數 ( L )(如交叉熵損失)。
(3)反向傳播
- 計算損失 ( L ) 對 ( A ) 和 ( B ) 的梯度
- 不計算( W ) 的梯度(因其被凍結)。
(4)參數更新
- 使用優化器(如Adam)更新
(5)迭代優化
- 重復步驟2-4,直到損失收斂或達到訓練輪次。
- 訓練完成后,( A ) 和 ( B ) 捕捉了任務特定的調整信息。
推理部署選項
- 合并權重:將 ( W' = W + A * B ) 合并為單一矩陣,直接用于推理(適合固定任務)。
- 動態加載:保持 ( W ) 和 ( A * B ) 分離,靈活切換不同任務的LoRA模塊(適合多任務場景)。
關鍵特點
- 參數高效:僅訓練 ( A ) 和 ( B ),參數量從 ( d * k ) 降至 ( (d + k) * r )。
- 內存節省:無需存儲全參數微調的梯度,顯存占用大幅降低。
- 兼容性:原始模型 ( W ) 保持不變,支持多任務共享。
LoRA可以用在Transformer的哪些層
LoRA是"好鋼要用在刀刃上"。并非模型的所有參數都需要微調,選擇關鍵層進行適配即可達到接近全參數微調的效果。LoRA目前主要可以應用在transformer中的以下兩類層:
Transformer是谷歌在2017年推出的深度學習模型,專門處理序列數據。簡單來說,序列數據就像排隊的小朋友,每個小朋友都有自己的位置和信息,Transformer能把這些信息處理得明明白白。后面有空我會專門出一個系列講解一下。
1. 注意力層(Self-Attention)
Transformer的核心是多頭注意力機制,每個注意力頭包含4個權重矩陣:
- ( W_q )(Query)
- ( W_k )(Key)
- ( W_v )(Value)
- ( W_o )(Output)
LoRA通常應用在:
- ( W_q ) 和 ( W_v )(最高優先級):
- 調整 ( W_q ) 可改變模型"關注哪些信息"。
- 調整 ( W_v ) 可影響"如何編碼關注的信息"。
- ( W_o )(次優先級):
- 調整輸出投影矩陣,但收益通常不如 ( W_q ) 和 ( W_v ) 顯著。
實驗結論(來自LoRA原論文):
- 僅微調 ( W_q ) 和 ( W_v ) 即可達到全參數微調效果的90%以上。
- 添加 ( W_o ) 的LoRA對性能提升有限(<2%),但會增加參數量。
2. 前饋網絡層(FFN)
FFN包含兩個線性變換:
- ( W_1 ):升維(通常放大4倍,如d_model → 4×d_model)
- ( W_2 ):降維(4×d_model → d_model)
適用場景:
- 大模型(如GPT-3):添加FFN層的LoRA可進一步提升性能。
- 復雜生成任務:調整FFN能增強任務特定的特征表達。
不推薦使用LoRA的層
(1)嵌入層(Embedding):
- 參數量大但微調收益低,凍結可節省資源。
(2)LayerNorm/Bias:
- 參數少,直接全參數微調成本低。
- LayerNorm的縮放因子和偏置本身具有低秩特性,無需LoRA。
實際配置建議
模型規模 | 推薦LoRA目標層 | 典型rank (r) |
小模型(如BERT) | 僅 ( W_q ), ( W_v ) | 8-16 |
大模型(如GPT-3) | ( W_q ), ( W_v ), FFN的 ( W_1 ) | 32-64 |
復雜生成任務 | 所有注意力矩陣 + FFN | 64+ |
模塊化設計優勢
- 任務切換:不同任務可獨立配置LoRA模塊(如翻譯任務用( W_q ), ( W_v ),摘要任務額外啟用FFN)。
- 資源分配:對關鍵層分配更高秩(如( r=32 )),次要層用低秩(如( r=8 ))。
LoRA訓練時需要調整哪些超參數
以 LLaMA-Factory 的配置為例,說明 LoRA 的關鍵超參數及其調參策略:
核心參數表
參數名 | 類型/范圍 | 含義 | 建議值 | 默認值 |
? | ? | 微調類型選擇 | 必須設為 ? | ? |
? (r) | 正整數 | LoRA的秩,決定矩陣A/B的列數/行數 | 簡單任務:8-16 | 8 |
? (α) | 正整數 | 縮放系數,控制ΔW對原始權重W的影響強度 | 通常設為 ? | None |
? | 0.0-1.0 | LoRA層的Dropout概率 | 大數據集:0.0 | 0.0 |
? | 逗號分隔的字符串 | 應用LoRA的模塊名稱(需匹配模型層名) | 默認:? | ? |
? | 逗號分隔的字符串 | 額外擴展的LoRA目標模塊(如FFN層) | 通常留空,大模型可加? | None |
調參技巧
- 秩(r)的選擇
- 小數據集(<5K樣本):r=8
- 大數據集(>50K樣本):r=32+
- 從小開始:優先嘗試r=8或16,逐步增加直至性能飽和。
- 數據量關聯:
- 目標層選擇策略
# 簡單任務(如分類)
lora_target = "q_proj,v_proj"
# 復雜任務(如生成)
lora_target = "q_proj,k_proj,v_proj,o_proj,ffn.w1,ffn.w2"3.改進技術的適用場景
- LoRA+:訓練速度要求高時啟用(設?
?lorapius_lr_ratio=8??)。 - DoRA:需要逼近全微調性能時開啟(?
?use_dora=true??)。 - rsLoRA:當r≥32時更穩定(?
?use_rslora=true??)。
參數影響對比
超參數 | 參數量影響 | 訓練速度 | 性能影響 |
? ↑ | 線性增加 | 略微下降 | 先升后平 |
? ↑ | 無影響 | 無影響 | 調節強度 |
? | 增加約10% | 下降10%-20% | 提升1%-3% |
? | 無影響 | 初始化耗時增加 | 收斂更快 |
經典配置示例
# GLUE任務(BERT-base)
lora_rank:16
lora_alpha:32
lora_target:"query,value"
lora_dropout:0.1
# GPT-3文本生成
lora_rank:64
lora_alpha:128
use_rslora:true
lora_target:"q_proj,v_proj,ffn.w1"總結
LoRA是一種高效的大模型微調技術,它通過低秩矩陣分解顯著地減少了參數量和計算資源的需求,同時又能保持接近全模型微調的性能。在接下來的文章中,我們將從實戰角度出發,借由Llama-Factory來進行模型微調。我希望能幫助讀者從零開始,全面掌握模型微調的知識和技巧。
本文轉載自??AI 博物院?? 作者:longyunfeigu

















