萬字綜述:全面梳理 FP8 訓練和推理技術 精華
一、背景
隨著 ChatGPT 的橫空出世,LLM/AIGC 領域迎來空前的關注,各類大模型如雨后春筍般出現,科技公司對 AI 算力的需求也呈爆發式增長。在這樣的背景下,如何在有限資源內提升模型訓練和推理效率成為研究的熱點。而在眾多的方向中 FP8 逐漸成為研究熱點,FP8 的應用落地也是一個極具潛力的方向。
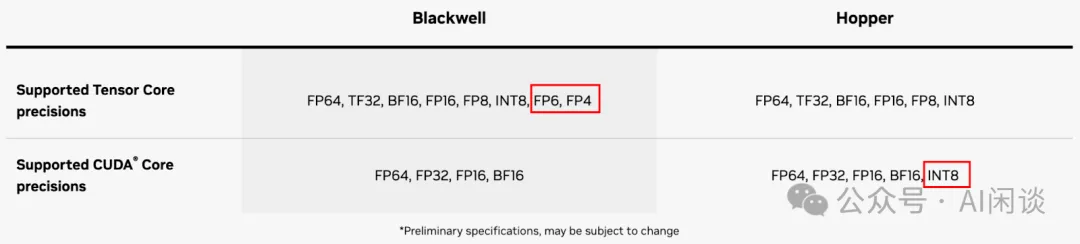
FP8 的重要性日益凸顯,很大程度上得益于 NVIDIA Hopper 架構和 Ada Lovelace 架構對 FP8 的硬件支持。最新發布的 Blackwell 架構更是進一步拓展了低精度范圍,支持了 FP6 和 FP4 格式。
業界對 FP8 的支持也在不斷深入,我們也一直在關注業內對 FP8 的支持情況。比如各種推理框架(如 vLLM、TensorRT-LLM)和訓練框架(如 Megatron-LM) 也都在增強對 FP8 的支持。然而,我們發現很多人依然對 FP8 存在諸多疑問和猶豫,比如 FP8 相比 INT8 有什么優勢,FP8 的各種表示方式(E5M2、E4M3、E3M4、E2M5)該怎么選擇,FP8 對模型精度和訓練/推理速度的影響有多大?
為了厘清這些問題,我們系統地梳理了最近幾年 FP8 相關的重要論文(主要來自 IBM、高通、微軟、Graphcore 和 NVIDIA 的 7 篇論文),旨在提供一個全面而深入的理解。本文將追溯 FP8 的演進歷程,分析其在 AI 領域的應用,并探討其可能帶來的變革。通過這一系列的探討,我們希望大家能更好地理解 FP8 技術,并為其在實際應用中的決策提供有力支持。
二、引言
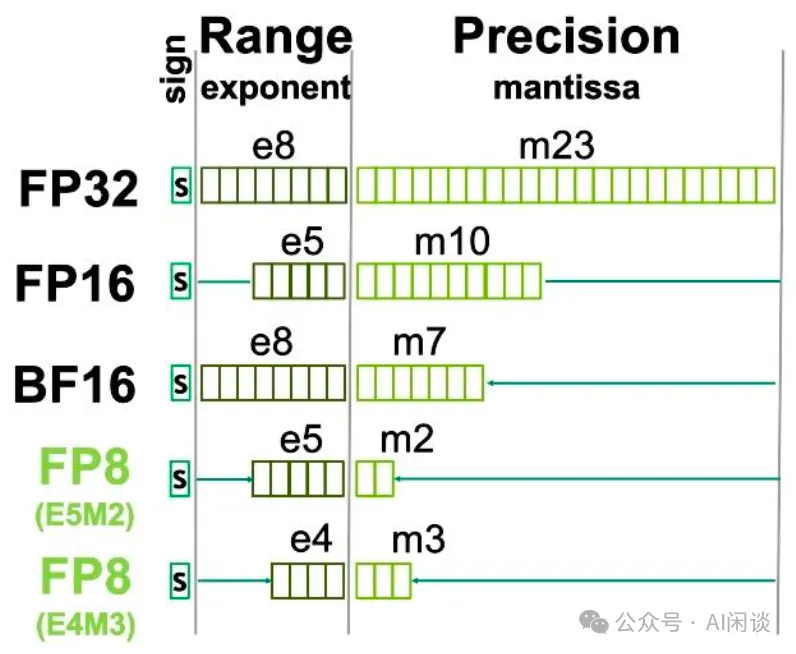
2.1 浮點數值表示
如下圖為 NVIDIA GPU 常見的浮點數表示方式,其中 sign 表示符號位,exponent 表示指數位(決定了動態范圍),mantissa 表示尾數位(決定了表示精度)。
- 相比 FP32:
FP16的指數位和尾數位都更小。因此,通常 FP32 轉 BF16 時會帶來較大的精度損失。
BF16的指數位和 FP32 相同,尾數位更少。因此,通常 FP32 轉 BF16 只需要做尾數位的截斷,損失相對較小。現在的 LLM 預訓練中通常都會使用 BF16。
- 相比 FP16:
- FP8 E4M3 的指數位和尾數位都更小。因此,通常 FP16 轉 FP8 E4M3 時會帶來較大的精度損失。
- FP8 E5M2 的指數位和 FP16 相同,尾數位更少。因此,通常 FP16 轉 FP8 E5M2 只需要做尾數位的截斷,損失相對較小。 ?
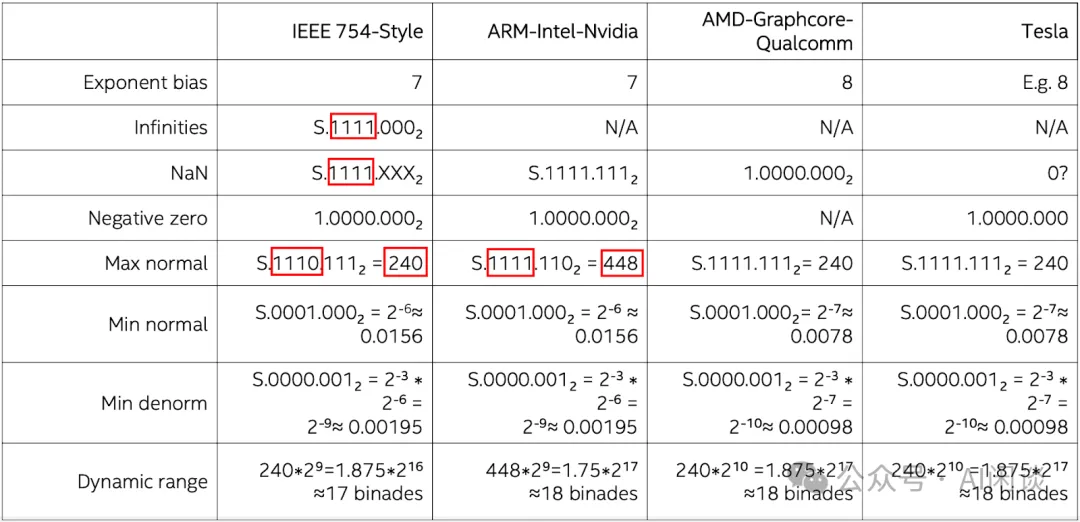
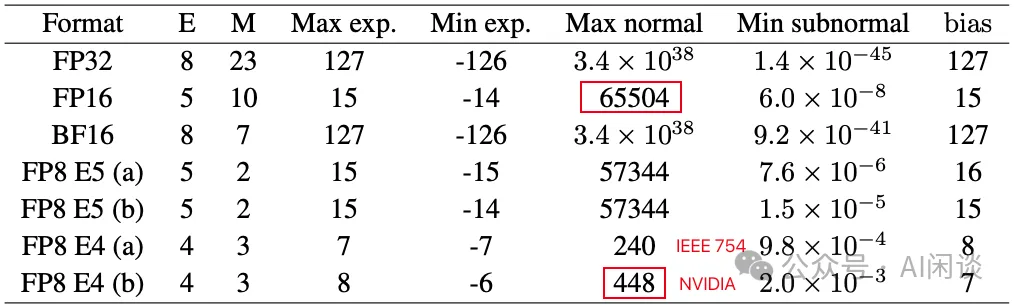
需要說明的是,雖然都是 E5M2 或者 E4M3,不同公司的硬件可能采用不同的格式。比如 NVIDIA GPU 上的 E5M2 符合 IEEE 754 Style,而 E4M3 卻不符合 IEEE 754 Style,本文中沒有特殊說明都以 ARM-Intel-Nvidia Style 為例。如下圖所示,IEEE 754 Style 的 E4M3 的范圍為 [-240, 240],而 ARM-Intel-Nvidia Style 的 E4M3 的范圍是 [-448, 448]:
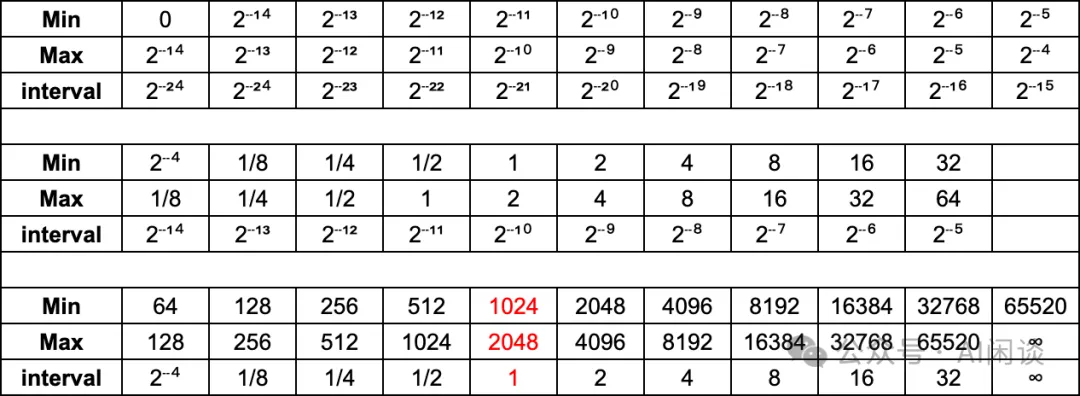
2.2 浮點數值精度
如下圖所示為 FP16 在不同數值區間的精度:
如下圖所示為 ARM-Intel-Nvidia FP8-E4M3 在不同數值區間的精度:
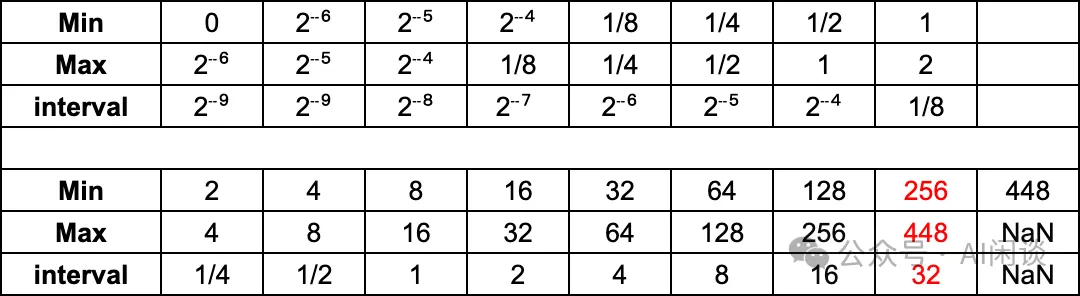
如下圖所示為 ARM-Intel-Nvidia FP8-E5M2 在不同數值區間的精度:
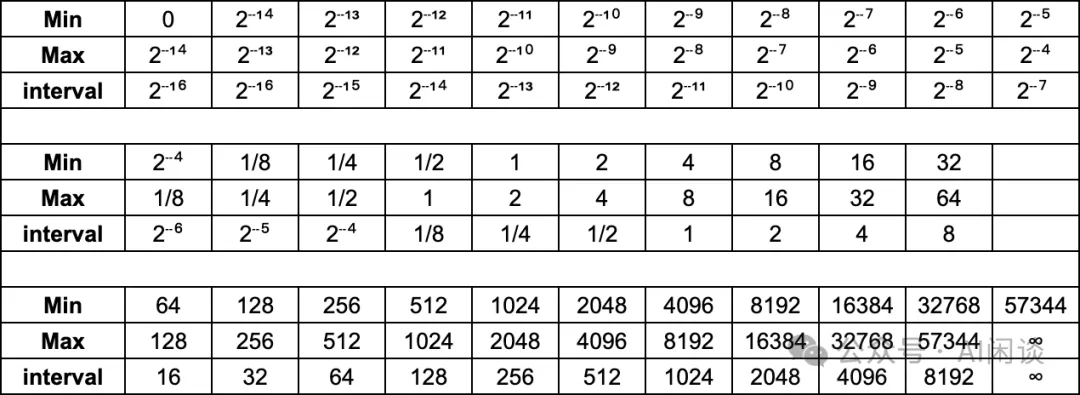
與傳統的 FP16 和 FP32 相比,FP8 可以顯著減少存儲,提高計算吞吐。對于 FP8 而言,在表示范圍內:
- E4M3 更精準:比如 [1, 2] 之間,E4M3 的最小間隔為 1/8,而 E5M2 的最小間隔為 1/4。
- E5M2 范圍更寬:比如 E4M3 的表示范圍為 [-448, 448],而 E5M2 的表示范圍為 [-57344, 57344]
2.3 舍入錯誤
浮點數的位數越低,越容易出現舍入誤差(大數吃小數)。以 FP16 為例,其在不同區間的精度是不同的,比如在 [1024, 2048] 之間,間隔只有 1,也就是如果是 1024.0 加上 1.5,其結果為 1025.0,如下圖所示為一個簡單的示例:
- 1024.6 用 FP16 表示時,將表示為 1025.0。
- FP16 的 1025.0 + FP16 的 0.4 = 1025.0。
- FP16 的 1025.0 + FP16 的 100.6 = 1126.0。?

2.4 FP8 Tensor Scaling
要將 FP8 應用于 LLM 的訓練和推理,其中的一個關鍵問題是如何克服表示范圍和精度下降相關的挑戰。其中的一個關鍵技術就是張量縮放(Tensor Scaling),如下圖 Figure 9 所示(圖片來自 [2310.18313] FP8-LM: Training FP8 Large Language Models),其核心是將不在 FP8 表示范圍內的數據縮放到 FP8 的表示范圍內。
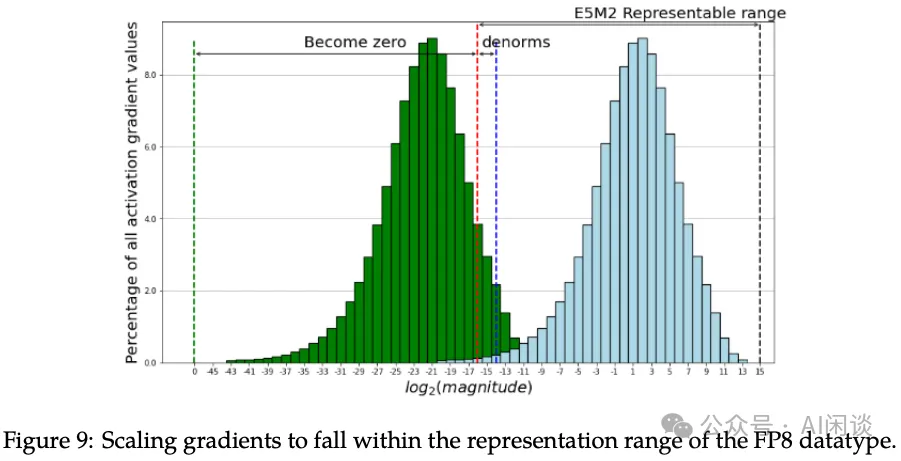
早期在 V100 和 A100 GPU 上的 FP16 混合精度訓練會廣泛采用全局損失縮放技術(Global Loss Scaling),很適合一些中小模型的訓練。然而,在處理一些超大模型或復雜任務時(例如 DALL-E 等模型),Global Loss Scaling 仍然會遇到嚴重的下溢問題(Underflow)。因此,越來越多采用 Block-wise 和 Layer-wise 的 Gradient 縮放。在 FP8 的 Per Tensor Scaling 技術中,有兩種常見方案:Just-in-time Scaling 和 Delayed Scaling(NVIDIA 在 Transformer Engine 中也有實現 Using FP8 with Transformer Engine)。
- Just-in-time Scaling(即時 Scaling):要做 Tensor 的 Scaling,首先需要計算 Tensor 絕對值的最大值(amax),然后得到 Scaling 值,再對 Tensor 進行 Scaling。中間的臨時存儲都是高精度的,可能要多次讀寫,計算和訪存開銷很大;此外,如果是分布式場景,比如梯度的 AllReduce,還要涉及分布式通信開銷。整體來說,額外引入的開銷會大幅降低 FP8 帶來的收益。
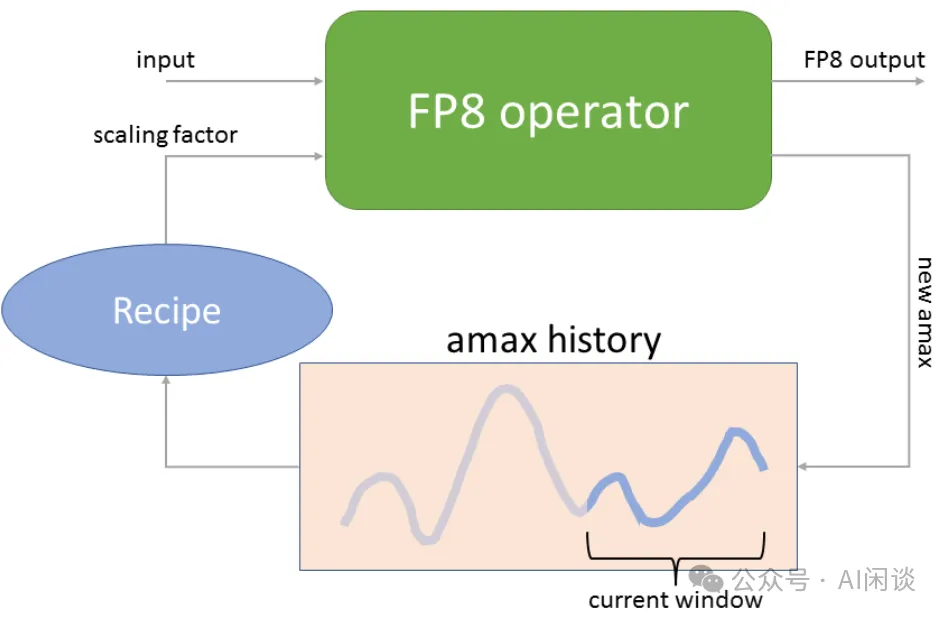
- Delayed Scaling(延遲 Scaling):其核心思路是使用額外的 Tensor 來存儲之前的 amax 歷史,然后根據歷史最大值決定當前的最大值。
如下圖為 NVIDIA Transformer Engine 中的 Delayed Scaling 實現方案,其 amax history 最多可以存儲 1024 個 history。在進行當前 Tensor 的 Scaling 操作時,會使用當前 Tensor 之前的 amax history 來預測當前的 amax(比如之前 history 的最大值),然后進行 Scaling 操作;Scaling 操作的同時會計算當前的 amax,并更新 amax history(PS:不確定這里是分成了兩個 Kernel 同時 Scaling 和計算 amax,還是融合為一個 Kernel)。
2.5 FP8 硬件支持
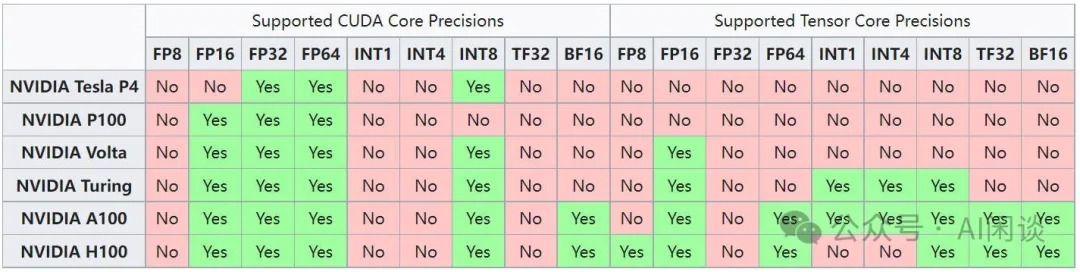
如下圖所示為常見 NVIDIA GPU 對不同數據類型的支持情況,可以看出,只有 Hopper 架構的 Tensor Core 才開始支持 FP8,CUDA Core 不支持。此外之后的 Ada Lovelace 架構和 Hopper 類似,也開始在 Tensor Core 支持 FP8。也就是說:
- A100 和 RTX 3090 都不支持 FP8。
- H100/H800 和 RTX 4090 的 Tensor Core 支持 FP8,但是 CUDA Core 不支持。也就是說,可以使用 FP8 的矩陣乘法(Tensor Core),但是不支持矩陣加法(CUDA Core)。?
如下圖所示,從 Hopper 架構開始,新的 Tensor Core 支持輸入兩個 FP8 的矩陣,然后以 FP8 格式相乘,并以 FP32 或 FP16 格式進行累加。Cublas 中也提供了相關 API 可以把后續的類型轉換融合進去,就可以避免 FP32 或 FP16 的中間結果寫回 Global Memory。
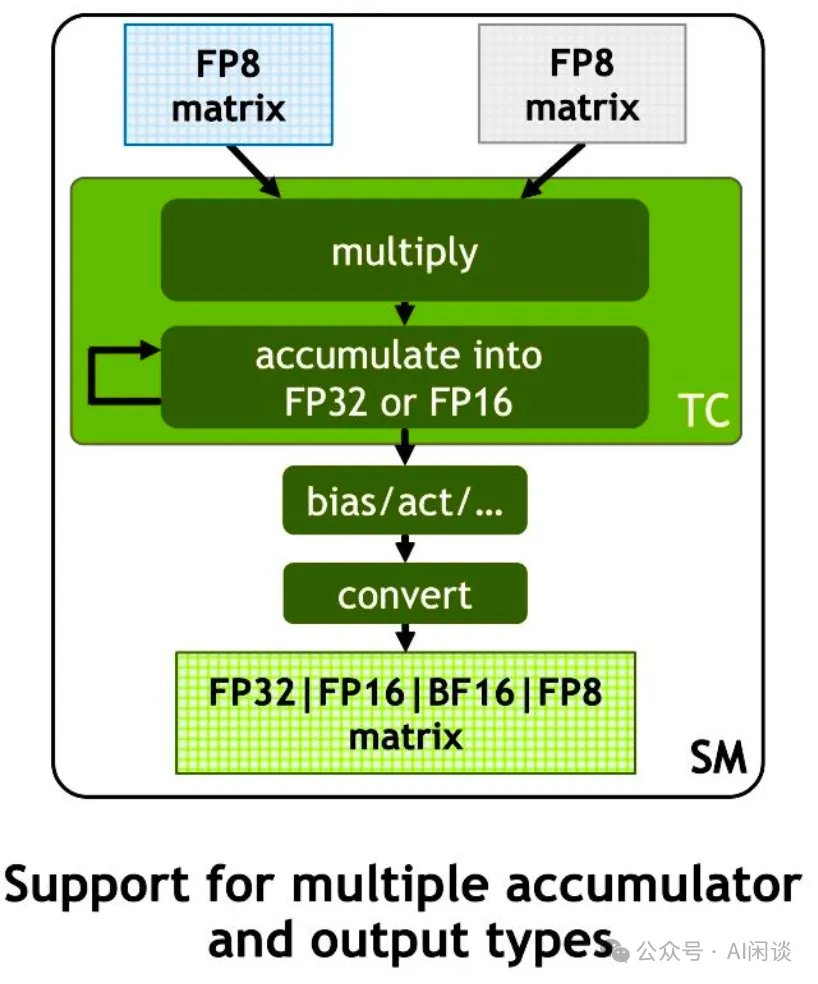
NVIDIA 最新發布的 Blackwell GPU 的 Tensor Core 相比 Hopper 進一步添加了對 FP6 和 FP4 的支持,而 Blackwell GPU 的 CUDA Core 不再支持 INT8。此外,從 Hopper 開始都不再支持 INT4。
2.6 FP8 軟件支持
Pytorch 從 2.1 版本開始引入 FP8 格式支持,具體來說增加了 “torch.float8_e4m3fn” 和 “torch.float8_e5m2” 兩種數據類型(torch.Tensor — PyTorch 2.3 documentation)。但是現在的 2.3 版本也依然在很早期的階段,比如很多計算還不支持 FP8,如下圖所示(`torch.float8_e4m3fn` does not support `torch.cat` · Issue #107256 · pytorch/pytorch · GitHub):

NVIDIA 的 Transformer Engine 庫添加了對 FP8 的支持,可以查看 Using FP8 with Transformer Engine。
最新發布的 FlashAttention3 也計劃開放對 FP8 的支持,可以查看 GitHub - Dao-AILab/flash-attention: Fast and memory-efficient exact attention。
Numpy 目前還不支持 FP8。
vLLM、TensorRT-LLM 以及 Megatron-LM 都在支持 FP8.
三、IBM FP8 Training DNN
3.1 摘要
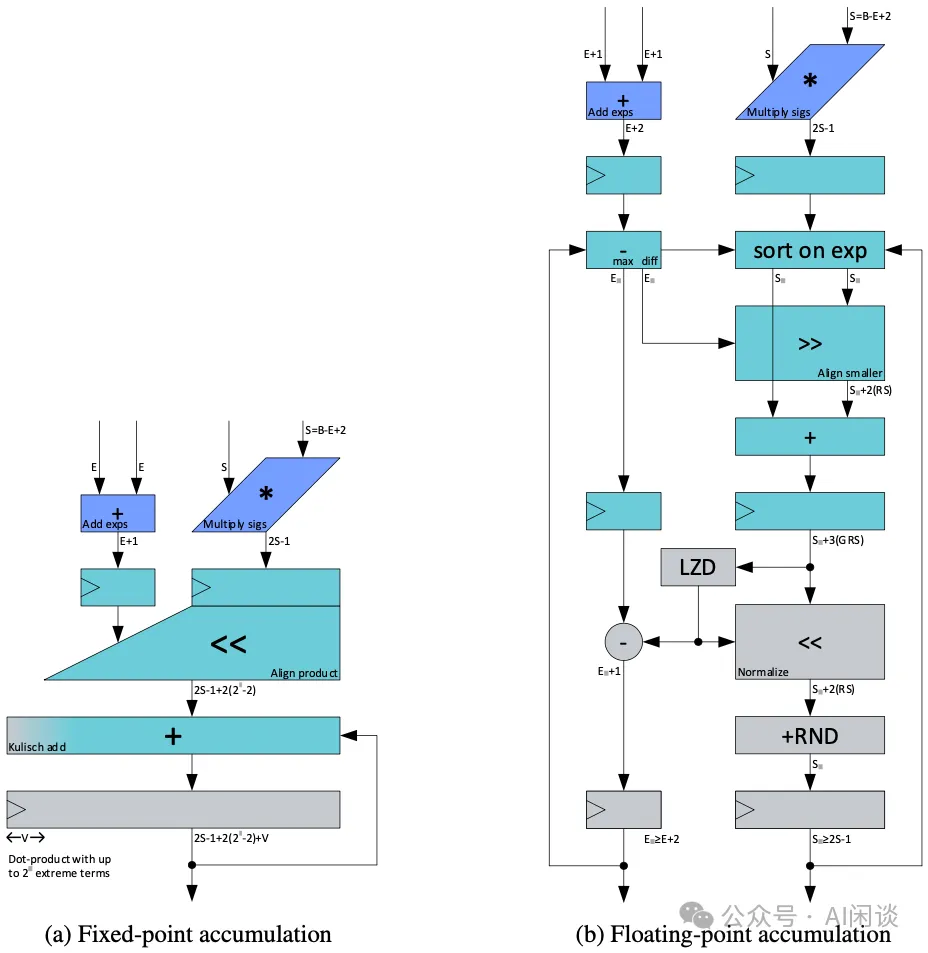
在 [1812.08011] Training Deep Neural Networks with 8-bit Floating Point Numbers 中,作者首次展示了使用 8bit 浮點數(FP8)成功訓練 Deep Neural Network 模型,并可以保持和 FP32 相當的精度。此外,作者還提出了基于塊的累積(Chunk Based Accumulation)和浮點隨機舍入(Stochastic Rounding)的方案,成功的將加法的算術精度(用于部分累積和權重更新)從 FP32 降低到 FP16。
需要說明的是:論文中使用的 FP8 為 E5M2 格式;此外,論文中的 FP16 為 E6M9 格式,而現在說的 FP16 通常為 E5M10 格式。
PS:論文發表于 2018 年,作者聲稱 FP8 可以比 FP16 獲得 2x-4x 的加速(考慮了芯片面積),但是當時的 NVIDIA GPU 還都沒有支持 FP8,因此并沒有在 NVIDIA GPU 進行實際的訓練測試。按照當前 H100 系列的 GPU 而言,一般也只能獲得不超過 2x 的加速。
3.2 方案
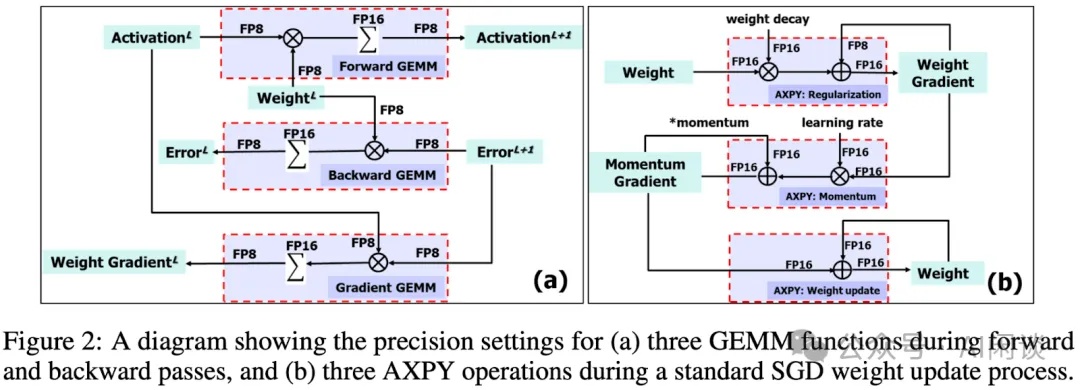
其訓練方案如下圖 Figure 2 所示:
- (a):前向和反向計算的 GEMM 操作都用 FP8作為輸入和輸出,但是在其累加的時候使用 FP16。
- (b):權重更新中的AXPY 都用 FP16 進行計算。?
3.2.1 基于塊的累積(Chunk Based Accumulation)
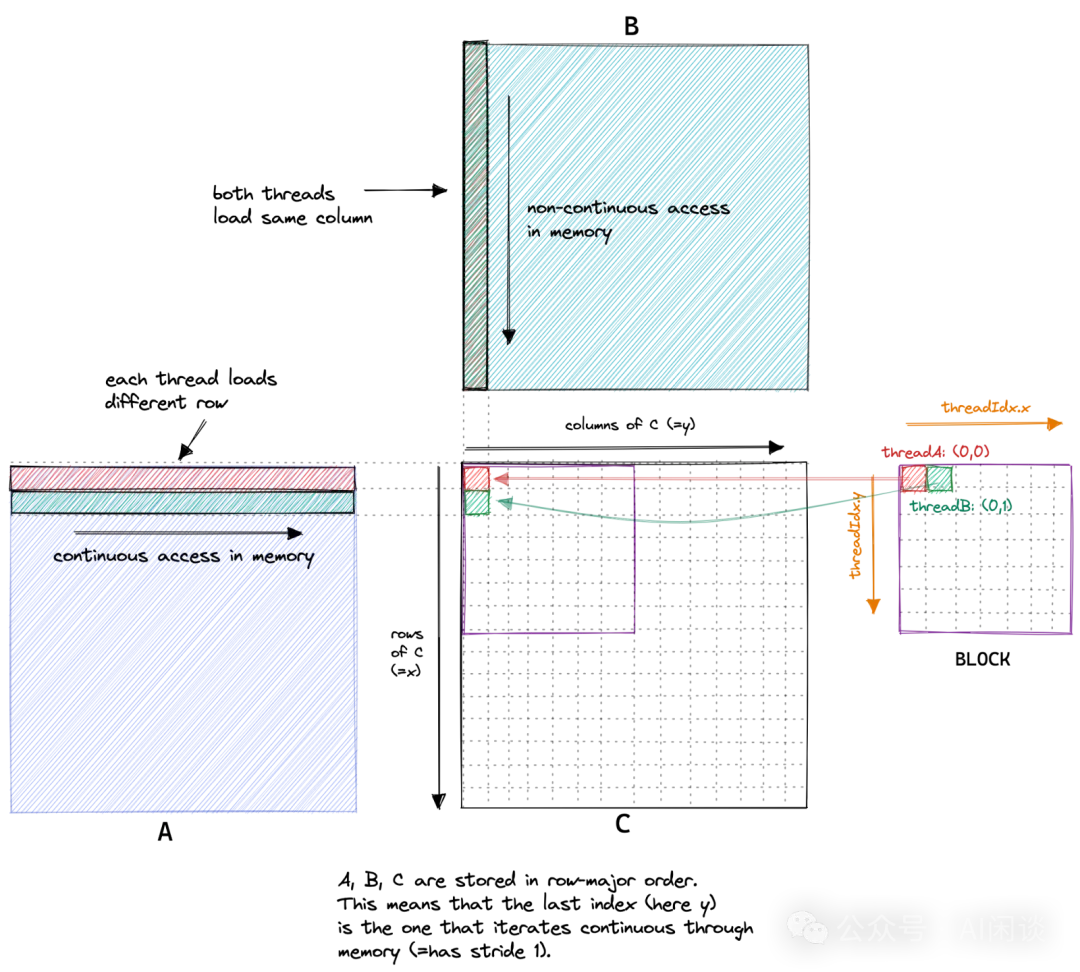
如下圖所示(圖片來自 How to Optimize a CUDA Matmul Kernel for cuBLAS-like Performance: a Worklog),對于一個 A*B=C 的矩陣乘法,C 中的每一個位置都是 A 中對應的一行與 B 中對應的一列的內積。比如 C 中的綠色塊(0, 1) 是 A 中第 1 行與 B 中的 0 列的內積。
而計算內積的過程可以等價于兩個向量的點乘加上一個向量的求和,而對一個 FP8 向量進行求和容易出現誤差。
- 通常的方式是有一個 sum 的值,所有結果都在 sum 上累加,這就容易出現上述介紹的大數吃小數問題,導致誤差逐漸變大。
- 實際上可以采用分塊的方式,如下圖所示,先在每個塊內累加,然后再將所有塊的和進行累加。(PS:由于在 GPU 中的矩陣乘法基本都是分塊計算,因此實現這種方案也就非常簡單)?
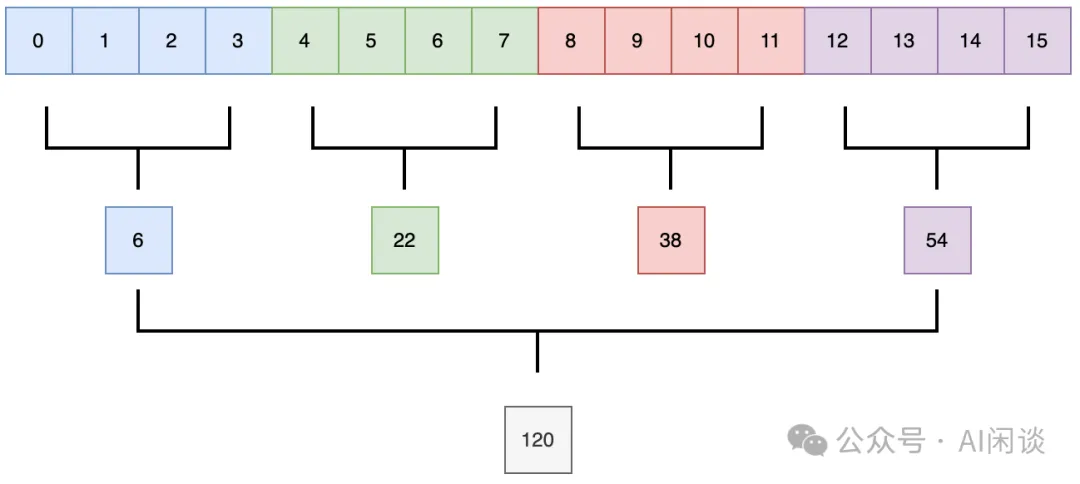
其偽代碼如下所示,比較簡單(也可以看出,其會額外增加很少的計算量):

3.2.2 浮點隨機舍入(Stochastic Rounding)
如下圖所示,作者也提出了隨機舍入的方案,具體來說,以差值與間隔的比例作為概率來向下或向上舍入(PS:可能需要特殊硬件的支持?):
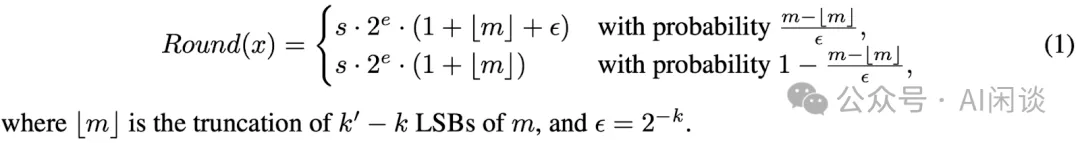
以 1025.0 + 100.6 為例,直接使用 FP16 計算將為 1125.0;而使用隨機輸入,其結果將有 0.6/1.0=60% 的概率為 1126.0,有 1-0.6/1.0=40% 的概率為 1125.0([1024, 2048] 之間的間隔為 1)。
3.3 實驗
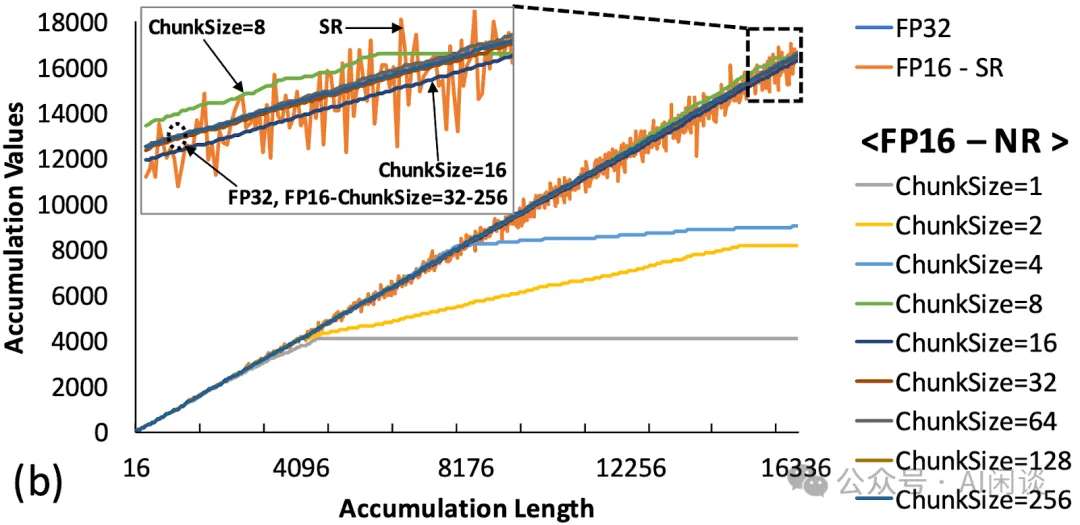
3.3.1 分塊和隨機舍入
如下圖所示,作者對比了分塊和隨機舍入在不同向量長度下的誤差,可以看出,當 ChunkSize 大于 8 之后就能很好的保持精度。同時,隨機舍入(FP16-SR)也能比較好保持精度,但相對波動也比較大:
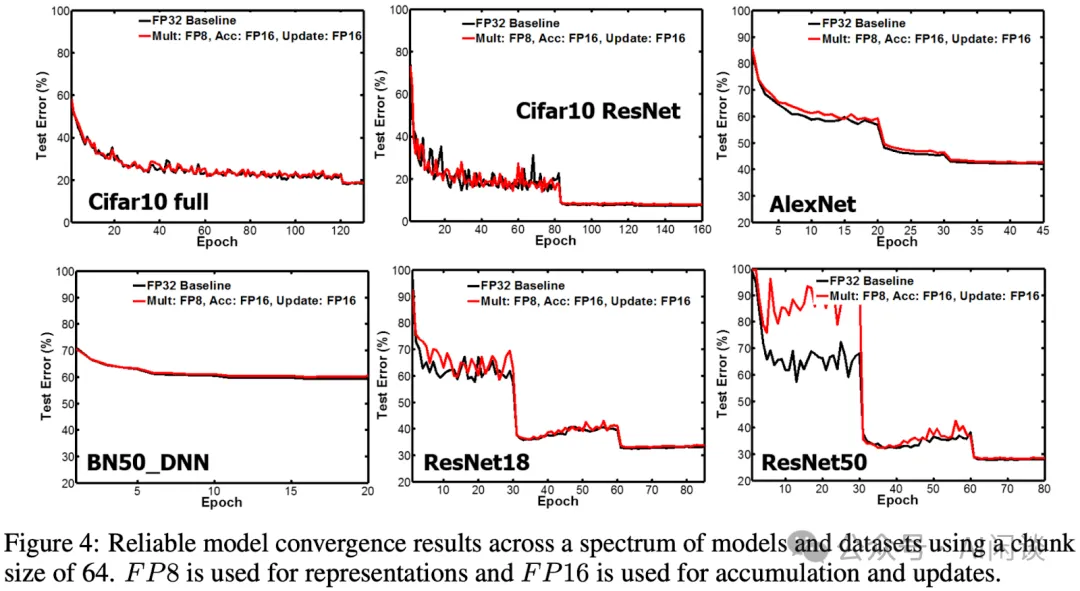
3.3.2 FP8 訓練
如下圖 Figure 4 所示,作者在多個 CV 任務上進行了訓練,其 FP8 訓練可以比較好的維持精度:
3.3.3 消融實驗
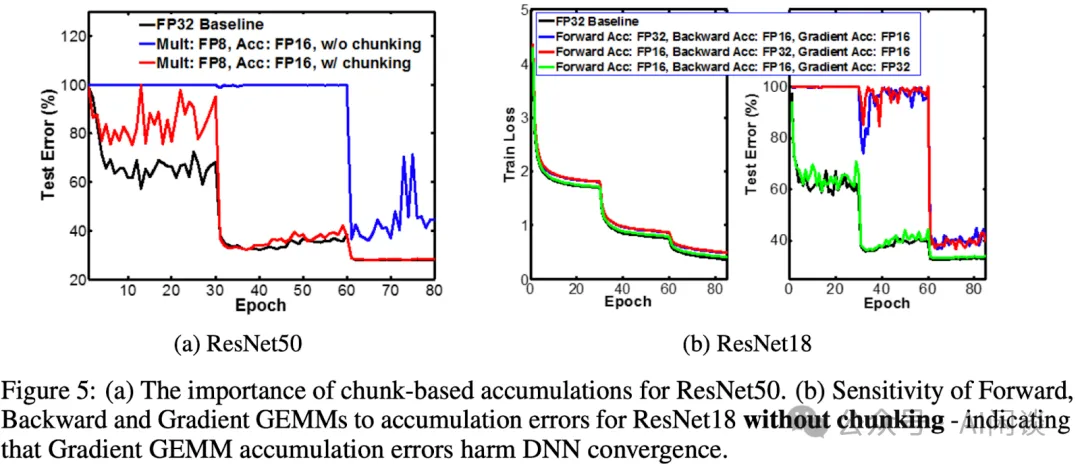
如下圖 Figure 5 所示,作者對比了不同配置的影響:
- (a):藍色表示不使用 Chunk的方式對精度影響較大,紅色表示使用 Chunk 方式后最后進步都能對齊。
- (b):紅色和藍色表示使用 FP16 進行梯度累加,對精度影響較大;綠色表示維持 FP32,完全能夠對齊。?
此外作者也對比了隨機舍入和最近鄰舍入的影響,可以看出,提出的隨機舍入能更好的維持精度:

四、IBM Hybrid 8-bit Floating Training and Inference
4.1 摘要
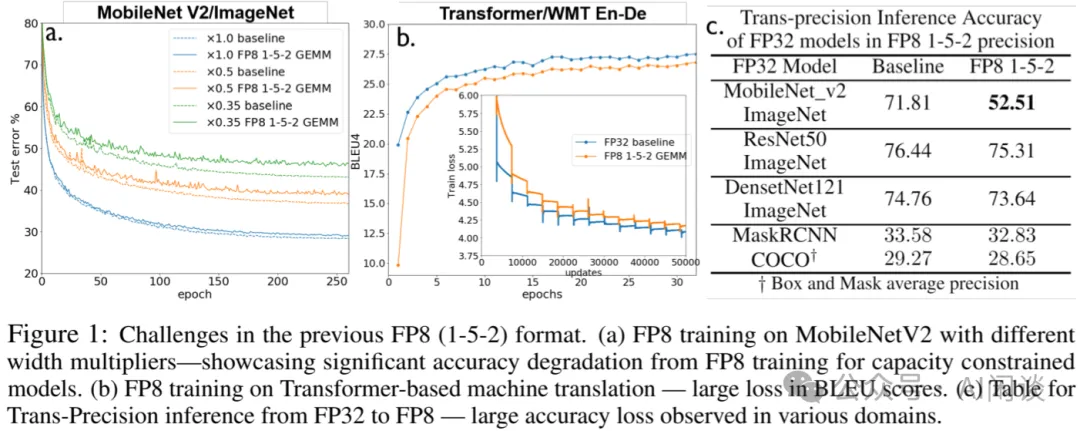
NIPS 2019: Hybrid 8-bit Floating Point (HFP8) Training and Inference for Deep Neural Networks 中,作者指出之前的工作(比如 IBM FP8 E5M2)中已經驗證了 FP8 用于 DNN 模型訓練,然而其只在少數模型上驗證,并不全面。此外,將 FP8 應用于 MobileNet 和 Transformer 等流行模型時,會觀察到顯著的退化,作者發現這種退化是因為前向傳播和反向傳播時對精度的要求不一致造成的。
基于以上發現,作者提出了一種混合 FP8(Hybrid FP8,HFP8)格式,并將其用于端到端的分布式模型訓練。作者使用 HFP8 在圖像分類、目標檢測、自然語言處理和語音在內的所有應用中進行 DL 模型訓練,驗證并不會降低準確性。此外,作者也發現提出的 HFP8 格式可以直接用于訓練后量化,只需簡單地微調以進行 Batch Normalization 的統計。
PS:本文中使用了 FP8 E4M3,但也不是標準的 ARM-Intel-Nvidia Style 或 IEEE 754 Style 的 E4M3,其自定義的 E4M3 的動態范圍只有 [-30, 30],最小值為 2-11,比標準的 E4M3 的 2-9 更小。
4.2 分析 & 方案
如下圖 Figure 1 所示,直接使用 FP8 E5M2 進行端到端訓練,在 MobileNet V2 和 Transformer 上訓練損失都比較大,而在 ResNet50、DenseNet121 和 MaskRCNN 上損失相對比較小:
作者通過實驗發現:
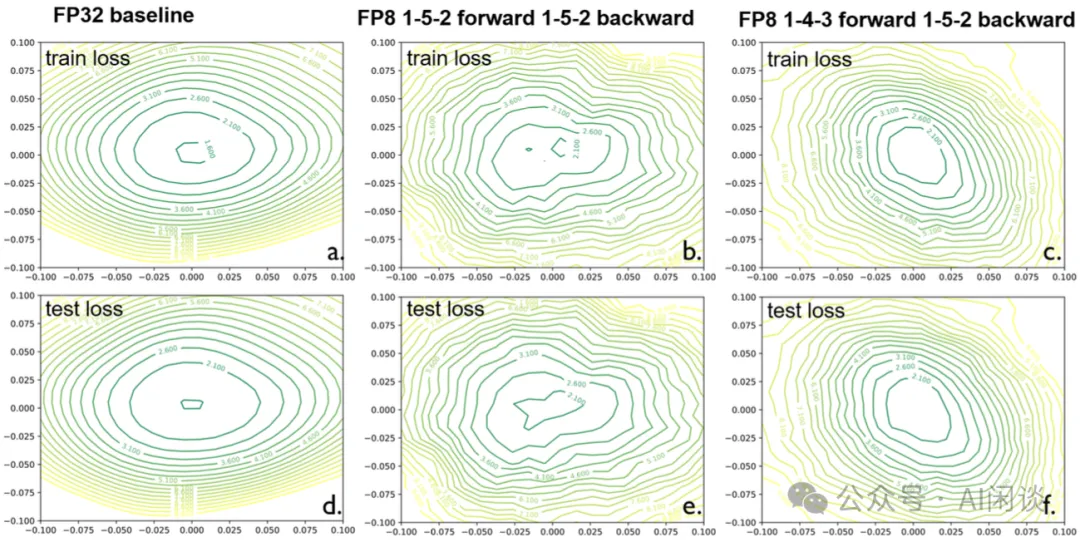
- 如下圖 b 所示:使用端到端 FP8 E5M2訓練時,Loss 曲面會出現多個鞍點,而且看起來更加的粗糙,這使得基于梯度下降的訓練變的不穩定。
- 如下圖 c 所示:在Forward階段使用FP8 E4M3訓練時(PS:這里使用的是自定義 E4M3,最小值可以達到 2-11,區間也更小,可以更好的保留 Weight 和 Activation 中比較小的值),可以顯著改善 Loss 曲面,變得更加平滑,使優化變得更加簡單。?
除此之外,作者也通過硬件設計實驗確認,同時支持 E4M3 和 E5M2 格式的浮點運算單元(FPU)的尺寸僅比只支持 E5M2 的單元大 5%,這表明混合格式在硬件上是可行的。
4.3 實驗
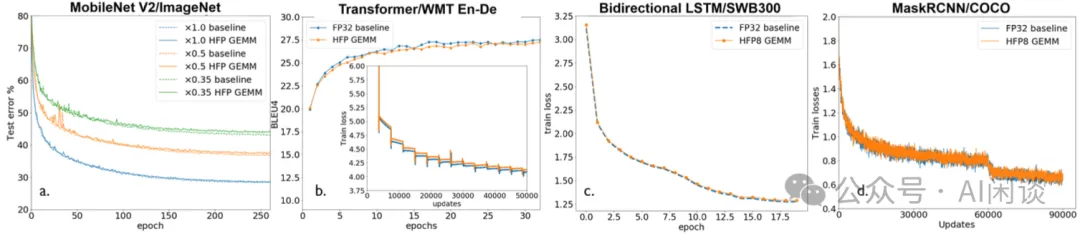
4.3.1 訓練實驗
如下圖所示,作者采用上述提到的混合 FP8 訓練范式,在常見的幾類任務上進行了訓練實驗,可以看出,提出的 HFP8 可以很好的維持精度:
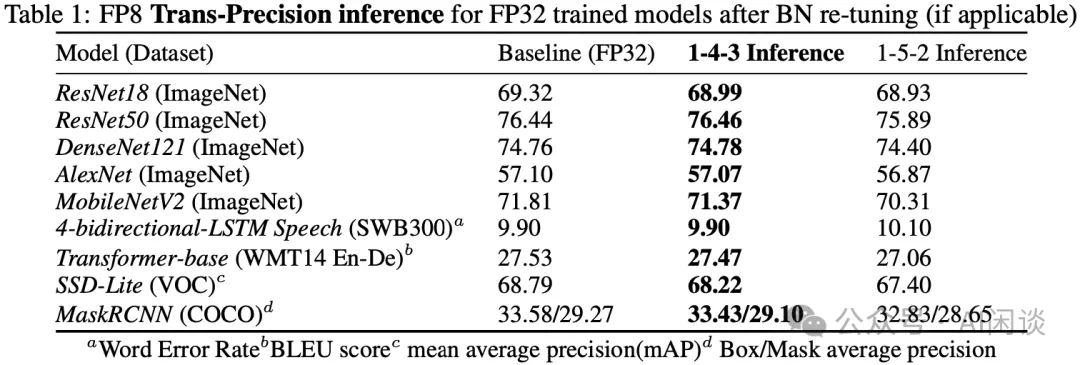
4.3.2 后量化推理實驗
如下圖 Table 1 所示,訓練后量化(Post Training Quantization,PTQ)推理中,帶有 BN re-tuning 的 FP8 E4M3 可以更好的維持精度:
五、NVIDIA FP8 Format for DL
5.1 摘要
NVIDIA 在 [2209.05433] FP8 Formats for Deep Learning 中具體介紹了 FP8 的兩種編碼方式:E4M3(4 位指數和 3 位尾數)和 E5M2(5 位指數和 2 位尾數)。其 E5M2 遵循 IEEE 754 規則來表示特殊值,而 E4M3 通過不表示無窮大并且只有一個 NaN 尾數位模式來擴展動態范圍。
作者進一步通過實驗驗證了 FP8 在 CNN、RNN 和 Transformer 模型上的性能,其所有超參數與 16bit 浮點數基線一致,結果表明 FP8 訓練可以很好的維持精度,和 16bit 浮點數基線相當。同時,作者也驗證了后量化方式(訓練 16bit,推理 FP8)同樣可以很好的維持精度。
PS:因為 NVIDIA GPU 不支持 IEEE 754 Style 的 E4M3,所以并沒有將其與 ARM-Intel-Nvidia Style 的 E4M3 進行對比實驗。
5.2 FP8 數據類型
如下圖 Table 1 所示,NVIDIA 的 E5M2 遵循 IEEE 754 規則來表示特殊值,所以其動態范圍和 IEEE 754 的 E5M2 一致。而 E4M3 中沒有無窮大,并且只有一個 NaN,這樣可以進一步表示 (256, 288, 320, 352, 384, 416, 448) 這幾個數字,將其動態范圍從 240 擴大到 448,這在 Deep Learning 領域非常有幫助:
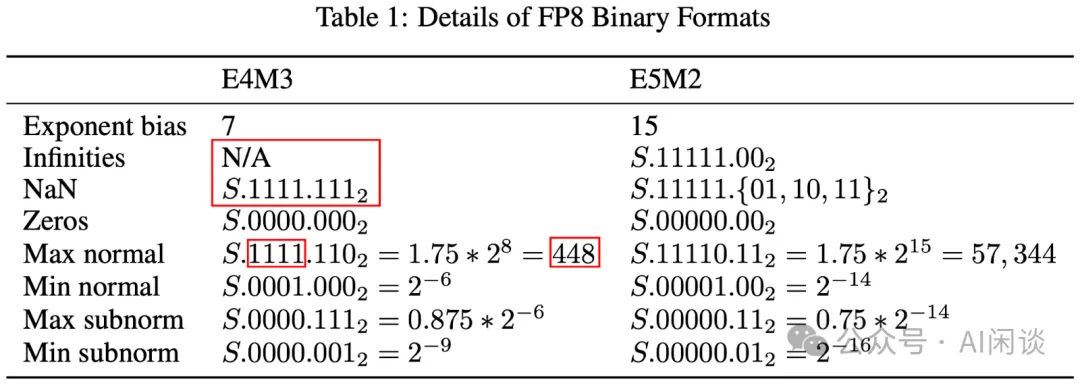
通常來說,Weight Tensor 和 Activation Tensor 會使用 E4M3,Gradient Tensor 會使用 E5M2。不過也有些模型只適合 E4M3 或者 E5M2。
5.3 實驗
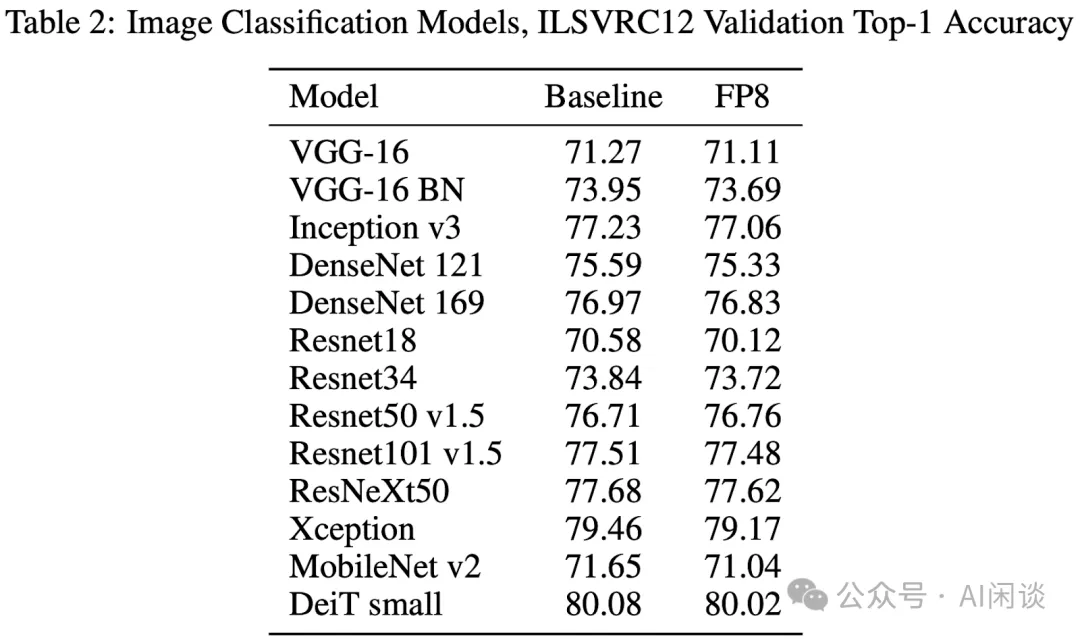
如下圖 Table 2 所示,作者驗證了一系列模型在 ImageNet 上訓練的精度,可以看出,FP8 訓練只比 Baseline 略低:
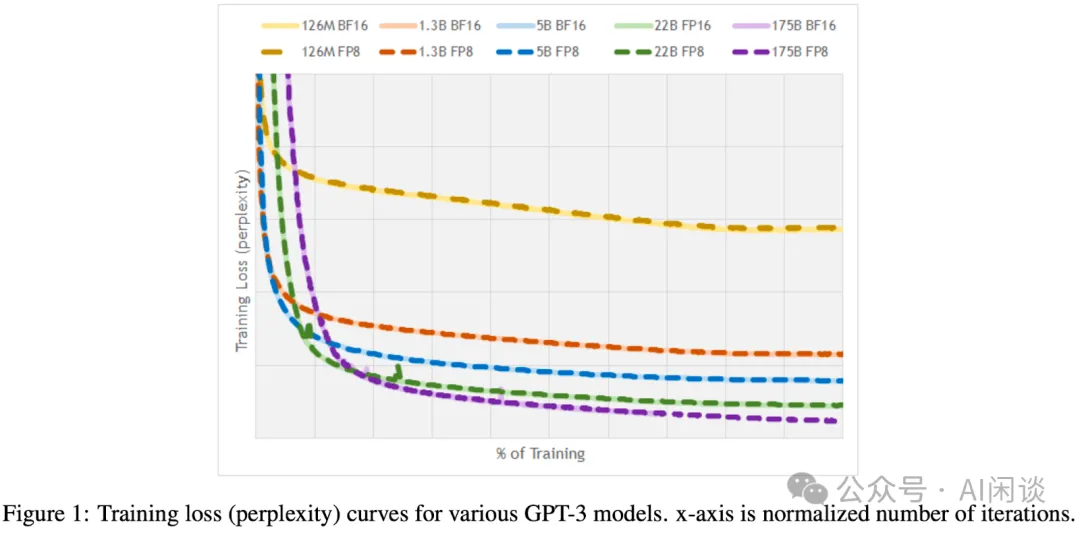
如下圖 Figure 1 所示,作者進一步驗證了不同規模 GPT-3 模型訓練的精度,可以看出,FP8 訓練和 FP16,BF16 訓練的 Loss 基本完全重合:
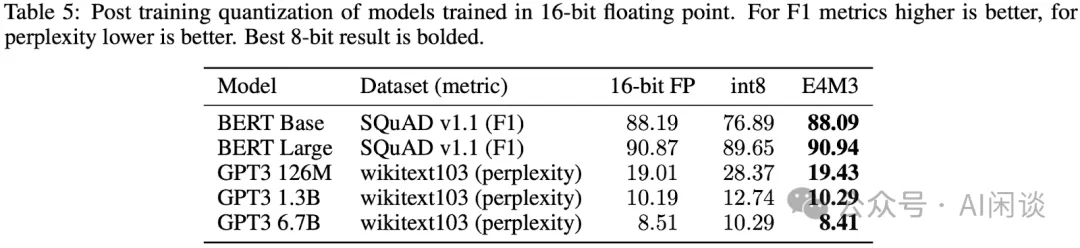
如下圖 Table 5 所示,作者進一步驗證了訓練后量化的精度,其中 Weight 采用 per Channel Scale,激活采用 per Tensor Scale。可以看出,FP8 E4M3 相比 INT8 可以更好的維持精度,基本無損:
六、高通 FP8 Quantization
6.1 摘要
在 [2208.09225] FP8 Quantization: The Power of the Exponent 中,高通的作者深入研究了浮點格式在神經網絡推理中的優勢。作者詳細介紹了 FP8 格式可以做出的選擇,包括指數和尾數的選擇(E5M2,E4M3,E3M4,E2M5),并具體分析了這些選擇在哪些配置下可以提供更好的性能。然后,作者也展示了如何將這些發現轉化為真實網絡,為 FP8 仿真提供有效實現,并提出了一種能夠學習 FP8 格式尺度參數和指數位數的新算法。
作者最終得出的結論是:在各種網絡中,對于訓練后量化(PTQ),FP8 格式的準確性優于 INT8,指數位數的選擇由網絡中異常值(Outlier)的嚴重程度決定。作者還進行了量化感知訓練(QAT),格式之間的差異會隨著模型的訓練而消失,可能是訓練減少了異常值的影響。
需要說明的是,這篇論文中的 FP8 采用的是 IEEE 754 Style,因此 E4M3 的動態范圍是 [-240, 240]。作者也想通過這篇論文證明 FP8 E2M5 和 E3M4 是更好的 FP8 格式,而不是 NVIDIA、Intel、AMD 和 IBM 普遍支持的 E4M3 和 E5M2。不過 LLM 的大熱似乎證明 E4M3 和 E5M2 是更正確的選擇。
PS:其實高通這篇論文比 NVIDIA 的 FP8 Format 早一個月,不過 NVIDIA 的論文中提到了對 FP8 E4M3 的擴展,有助于我們理解高通這篇論文中使用的 IEEE 754 Style 的 E4M3,因此我們將 NVIDIA 的 FP8 Format 其放在前面介紹。
6.2 預期量化誤差
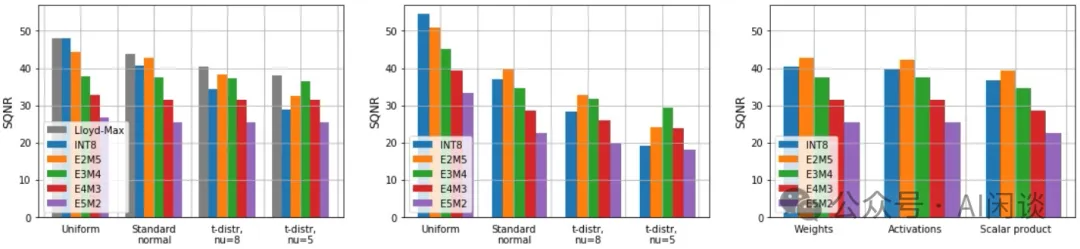
如下圖所示,作者分析了不同數據格式在均勻分布(Uniform)、高斯分布(Standard)和 t 分布(Student t)下的量化誤差(SQNR Signal to Quantization Noise Ratio),SQNR 越高越好。可以看出:
- 均勻分布、高斯分布:基本上 INT8 和 E2M5 可以獲得更高精度,并且FP8 中指數位越小,精度越高,也就是 E5M2 最差。
- t 分布:相比高斯分布存在更嚴重的長尾,此時反而 E3M4 獲得了更好的精度。(PS:對于 LLM 這種存在嚴重 Outlier 的場景,E4M3 和 E5M2 更合適)?
6.3 訓練后量化結果
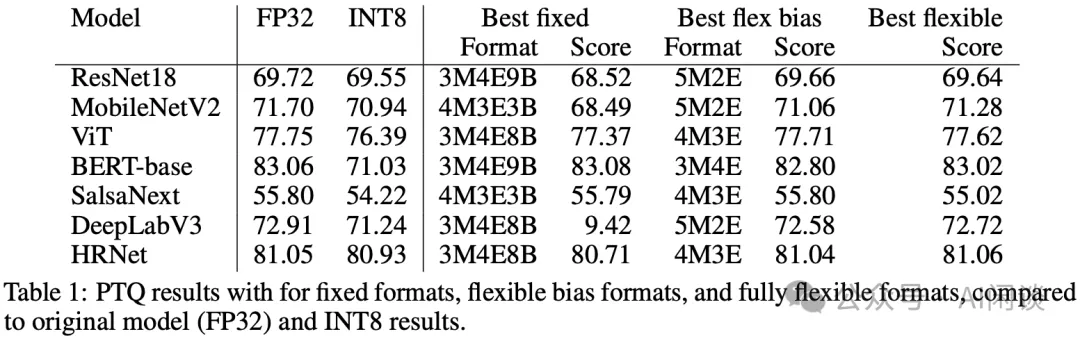
作者是在 A100 和 V100 GPU 上進行訓練后量化推理實驗,都不支持 FP8,下述的 FP8 都是模擬的結果。此外,作者對比了三種 FP8 量化方案:
- fully fixed format:整個模型都使用固定的尾數 m,指數 e 和 Bias b。
- best flexible bias format:整個模型使用固定的 m 和 e,但是 b 會按 Channel 或 Tensor 調整。
- fully flexible format:每個 Tensor 有對應的 m 和 e,每個 Channel 有對應的 b。
結果如下圖 Table 1 所示:
- 對于有更多 Outlier 的模型(ViT、Bert、SalsaNext 和 HRNet)需要 FP8 具有更多的指數位,以便支持更大的動態范圍。
- Best flexible往往獲得最優效果。
- BERT-base上INT8 的損失比較大,而 FP8 的幾種方式都損失比較小。?
6.4 量化感知訓練結果
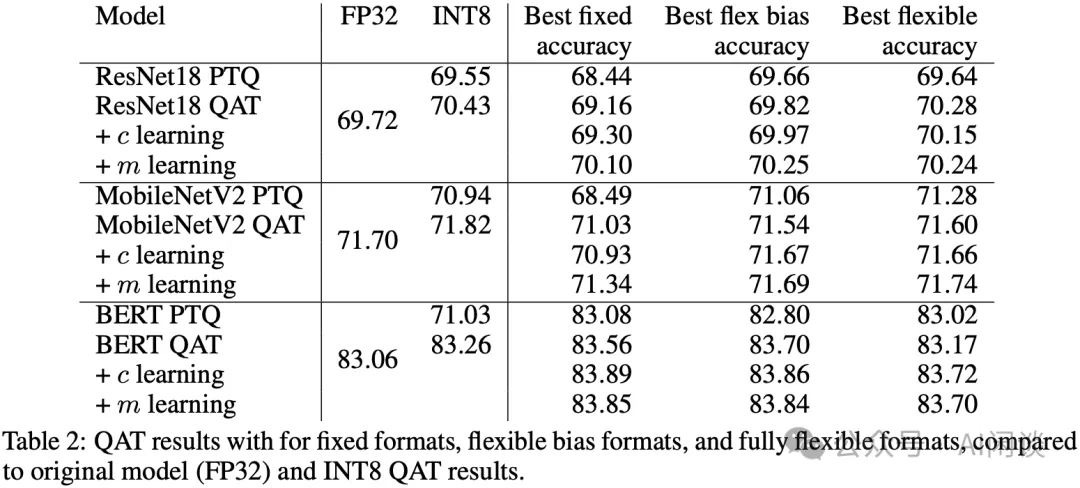
如下圖 Table 2 所示,通過量化感知訓練,不論是 INT8,還是各種格式的 FP8 都能比較好的維持精度。通過學習 c(表示 INT8 中的最大值) 和 m(FP8 尾數位) 的方式,甚至可以進一步提升精度:
七、高通 FP8 versus INT8 for Inference
7.1 摘要
[2303.17951] FP8 versus INT8 for efficient deep learning inference 是高通團隊對上面的 FP8 Quantization 工作的延續。作者還是想證明 FP8 E4M3 和 FP8 E5M2 在性能和準確性方面不能替代 INT8 進行深度學習推理,并通過實驗說明大部分模型中,FP8 E4M3 和 FP8 E5M2 比 INT8 更差。對于 PTQ 的極端情況,比如層中有顯著的異常值(Outlier)時,FP8 E4M3 和 FP8 E5M2 在準確性方面可能更好。此外,即使對于 INT8 不占優勢的 Transformer 模型,也可以使用 W8A18 的混合精度運行,或者通過量化感知訓練來彌補 INT8 的準確性問題。
除此之外,作者也提到在硬件中實現 FP8 的代價更大,其 FP8 單元的效率可能比 INT8 低 50%-180% 不等,如果 Workload 受計算限制,芯片的速度會明顯變慢。(PS:不過 NVIDIA 的 H100 中 INT8 和 FP8 的算力是相同的)
最后,作者提到當論文發表時,FP8 的各種方案還不太成熟,而 INT8 相關的方案卻已經存在多年,想進一步論證 INT4-INT8-INT16 為最好的解決方案。
7.2 硬件考量
如下圖所示為一個矩陣乘法的 accelerator 的概覽,作者認為 FP8 的標準還沒有確定,導致 FP8 accelerator 的設計存在很多種可能。比如,其中的 Accumulator 可以是 FP16 或者 FP32,計算完之后可能還需要再進一步量化為 FP8 才能被下一次計算使用。除此之外,除了矩陣乘法之外的很多 OP 也都是以 FP16 計算的,比如 Softmax。這樣對于一些 Memory Bound 的任務而言可能 FP8 計算也并不會有顯著的加速效果。(PS:事實上,通常會有一些高性能的 Kernel 實現,可以將這些操作融合,避免中間結果寫回 Global Memory,還是很有幫助的)
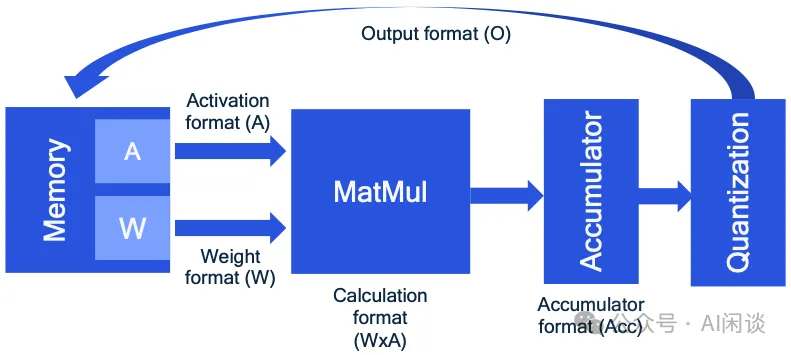
除此之外,如下圖所示,作者也想證明 FP8 相比 INT8 在硬件實現上更加復雜,可能會占據更大的電路面積,也就意味著同樣算力下,FP8 功耗可能更高。比如與 INT8 相比,FP8 E4M3 會增加 53% 的成本(PS:這也與 Meta 和 Microsoft 的結論類似 [2302.08007] With Shared Microexponents, A Little Shifting Goes a Long Way),如果進一步使用 FP32 進行累加,成本更是高達 183%。然而,NVIDIA 并沒有具體介紹其 FP8 的硬件設計,我們也無法考證,但至少在 NVIDIA 的 GPU 中,FP8 算力通常是與 INT8 一致的。
7.3 訓練后量化
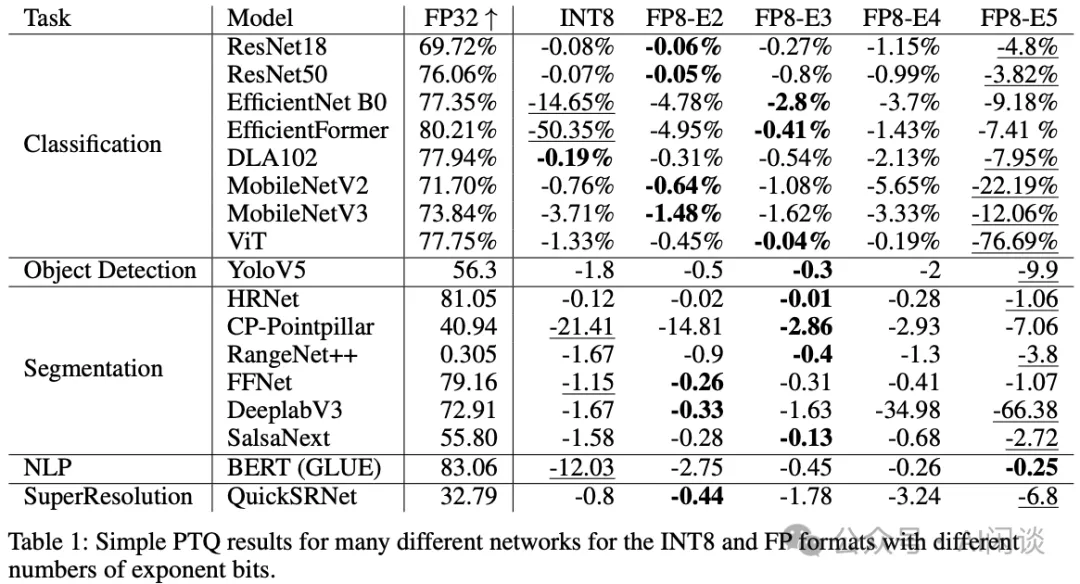
如下圖 Table 1 所示,作者進一步對比了 FP8 各種格式和 INT8 的訓練后量化精度,試圖證明 FP8 E2M5 和 E3M4 是更優的方案,從結果中可以看出,對于傳統的 CV 類模型也確實如此(現在也有很多基于 Transformer 的視覺模型)。然而,對于 BERT 模型,FP8 E5M2 和 E4M3 反而更優(PS:對于 Transformer 模型而言,NVIDIA 的 E5M2 和 E4M3 確實是更正確的選擇)。
7.4 Transformer 模型 INT8 校正
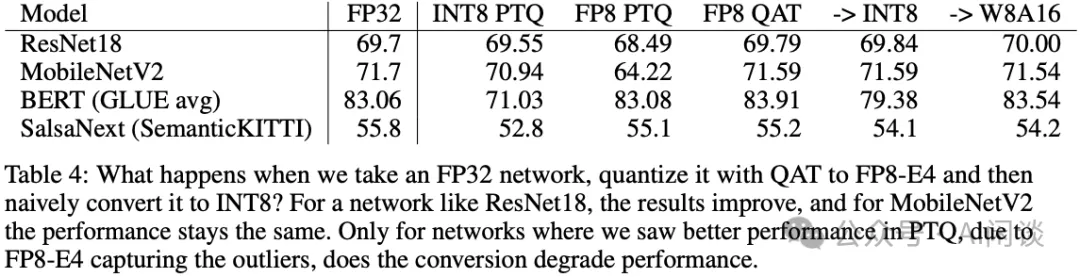
針對 INT8 不友好的 Transformer 模型,作者進一步探索了修正方案。如下圖 Table 4 所示,作者進一步探索了 FP8 訓練后的模型轉換為 INT8 推理,發現其相比直接從 FP32 轉換的精度會更高,而且使用 W8A16 后基本無損。除此之外,直接使用 INT8 量化感知訓練也可以很好的維持精度。
八、Graphcore Training and Inference LLM using FP8
8.1 摘要
Graphcore 團隊也針對 LLM 場景對 FP8 進行了深入的研究,在論文 [2309.17224] Training and inference of large language models using 8-bit floating point 中作者針對 FP8 的縮放問題進行了深入的探討,并提出了一種針對 FP8 Linear Layer 的尺度縮放方案 FP8-AMAX,其會基于每個權重、梯度和激活的 Tensor 來動態更新 scale。基于這種方案,作者對 LLaMA 2 和 GPT 模型進行了訓練和推理的驗證,其模型規模從 111M 到 70B 不等,實驗表明,其提出的 FP8-AMAX 可以很好的維持精度。
PS:本文作者主要聚焦在 FP8 E4M3 和 FP8 E5M2,和 NVIDIA 中的 FP8 格式一致。
8.2 Linear Layer 適配 FP8
8.2.1 FP8 推理
如下圖所示,由于 FP8 E4M3 的數據范圍遠小于 FP16,此外如果是 E5M3 和 E5M2 的矩陣乘,并使用 FP16 進行累加,也可能超出范圍,因此一般需要使用 Scaling 來避免上溢出或下溢出。
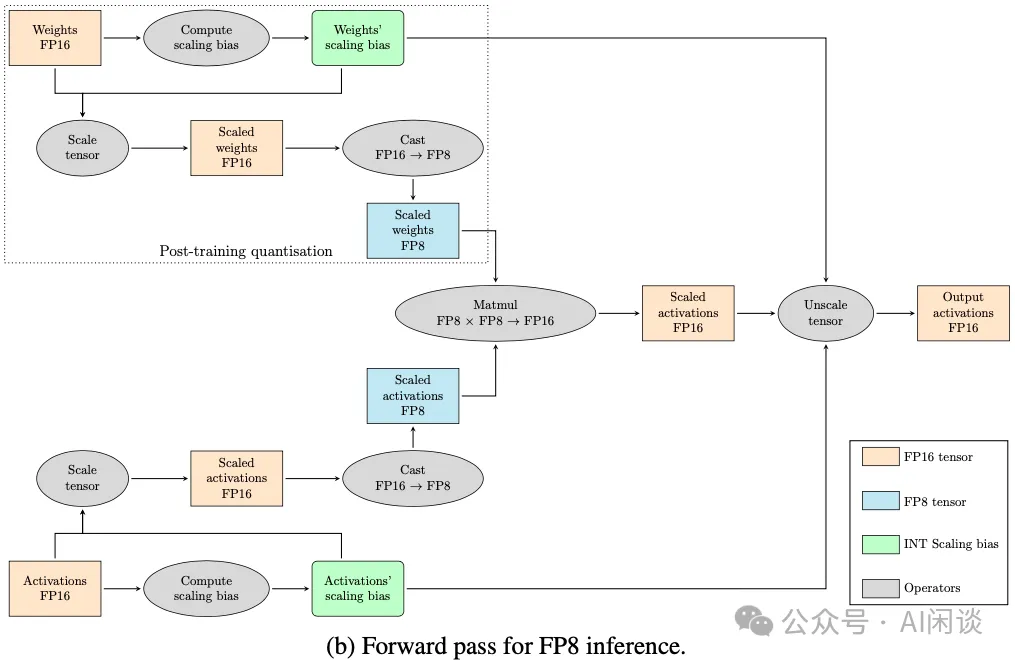
如下圖以 FP8 Inference 的過程為例,針對 FP16 的 Weight 和 Activation 都需要先計算 Scaling bias,然后進行 Scale 操作,之后再進行 Cast FP16 -> FP8 操作即可得到 Scale 后的 FP8 Weight 和 FP8 Activation(對于 Weight 和 Activation 通常轉換為 FP8 E4M3),執行完 FP8 的矩陣乘法之后還需要依賴上述獲得的 Scaling bias 來執行 Unscale 操作。需要指出的是,對于 Inference 而言,只用對 Weight 執行一次 Scale,然后保存 FP8 的 Weight 和 Scaling bias 即可。
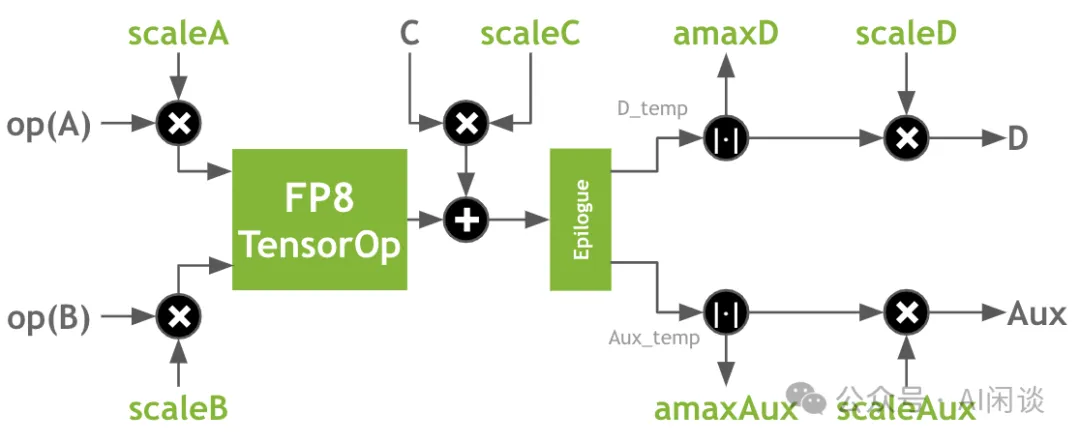
如下圖所示,新版本 cuBLAS 中已經支持了 Transformer 中的這種復雜計算:
8.2.2 FP8 訓練
在訓練階段 Weight 會不斷更新,通常需要過一段時間(step)就重新計算 Scaling bias。在訓練的 Backward 階段需要分別針對 Weight 和 Input Activation 計算 Gradient,這兩個操作都可以使用 FP8 矩陣乘加速,不過 Gradient 通常會表示為 FP8 E5M2。
此外,如果使用 BF16 或 FP32 (數據范圍一致)進行累加,則不必進行 loss scaling,如果使用 FP16 進行累加,通常需要使用 loss scaling,以便能夠更好的保留 Gradient。FP8-FP16 混合精度訓練的 loss scaling 方法和 full FP16 訓練中的一樣。
8.3 實驗
8.3.1 策略
作者采用了兩種計算 Scaling bias 的策略:
- FP8-AMAX:每一個 Linear Layer 的每一個 Batch 或者每一個 Tensor 都獨立計算 Scaling bias。
- FP8-CSCALE:所有 Weight、Activation 和 Gradient 共享相同的 Scaling bias。
8.3.2 FP8 推理
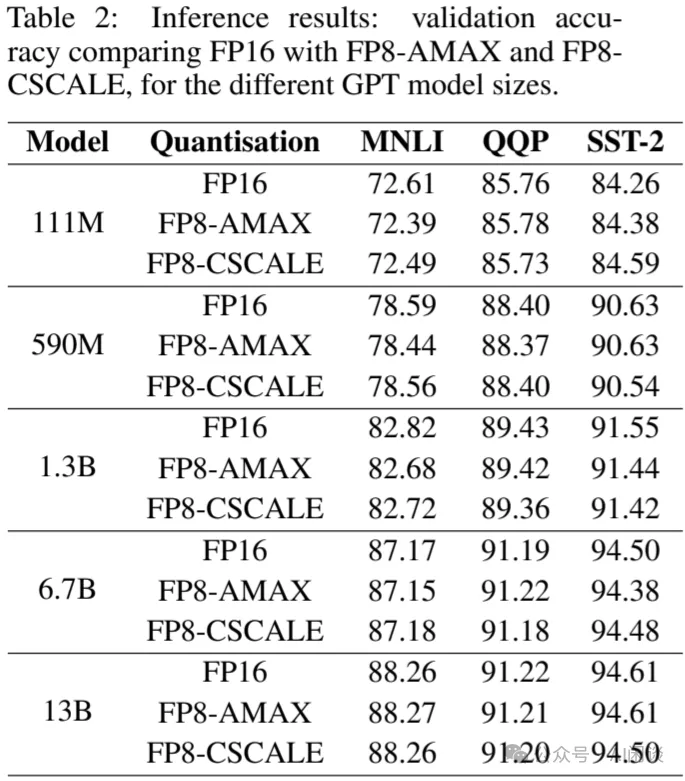
如下圖 Table 2 所示,使用 FP8-AMAX 或 FP8-CSCALE 推理相比 FP16 都能很好的維持精度,平均可以達到 FP16 的 99.5% 以上:
當然,使用 FP8-CSCALE 時,其 Scaling bias 需要在如下圖 Table 3 所示的范圍內,否則也會出現比較大的偏差:
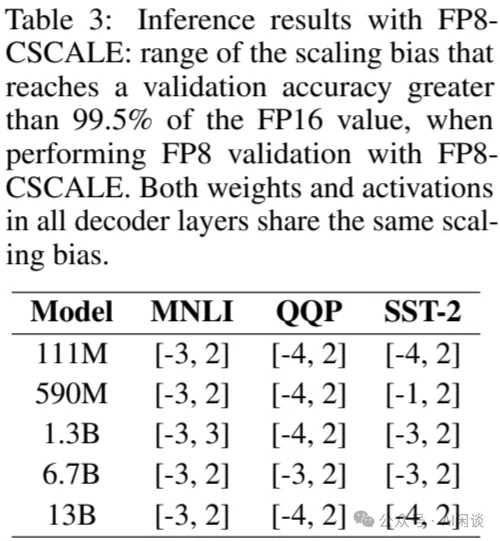
8.3.3 FP8 訓練
如下圖 Table 5 所示,作者進一步驗證了使用 FP8-AMAX 進行微調的精度,可以看出基本與 FP16 相當:
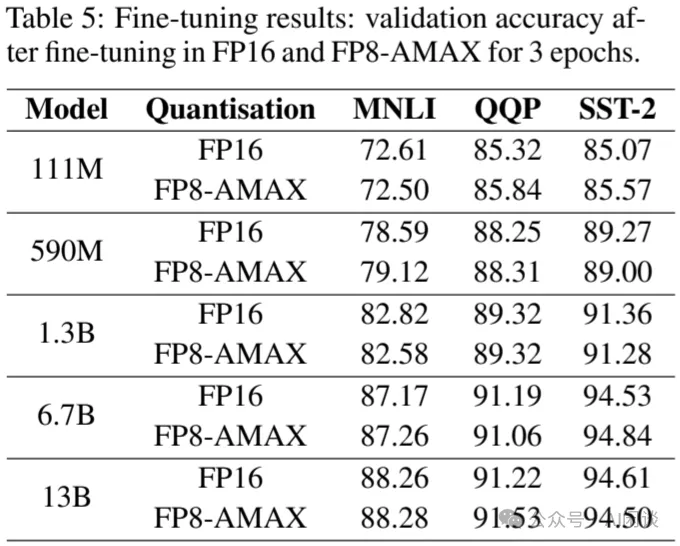
除此之外,使用 FP8-CSCALE 時,其 Scaling bias 需要在如下圖 Table 6 所示的范圍內,才能保證平均達到 FP16 99.5% 以上的精度,否則也會出現比較大的偏差。而且,模型越大,范圍會越小:

九、微軟 FP8-LM:Training FP8 LLM
9.1 摘要
在 [2310.18313] FP8-LM: Training FP8 Large Language Models 中,微軟的作者探索了 FP8 用于 LLM 的高效訓練。作者發現,在 LLM 訓練中大部分變量(例如梯度、優化器狀態)都可以采用低精度數據格式,而不會影響模型準確性,也不需要更改超參數。具體來說,作者提出了一種新的 FP8 自動混合精度 LLM 訓練框架。該框架提供 3 個級別的優化,以簡化 LLM 的混合精度和分布式并行訓練,包括 FP8 通信、FP8 優化器和 FP8 分布式并行訓練。
實驗表明,在 H100 GPU 上訓練 GPT 175B 模型,提出的 FP8 混合精度訓練框架可以降低 42% 的內存占用,而運行速度比廣泛采用的 BF16 最多快 64%,甚至比 NVIDIA 的 Transformer Engine 的速度快 17%,大幅降低 LLM 的訓練成本。此外,提出的 FP8 混合精度訓練時是通用的,可以無縫應用于其他任務,例如 LLM 指令微調和具有人工反饋的強化學習。
對應的開源開源代碼庫為:GitHub - Azure/MS-AMP: Microsoft Automatic Mixed Precision Library
PS:因為直接使用的 H100 GPU,所以對應的 FP8 E5M2 和 E4M3 為 ARM-Intel-Nvidia Style 的。
9.2 FP8 LLM
在作者研究 FP8 訓練 LLM 的時候,NVIDIA 的 Transformer Engine 只支持 Transformer 模型中的 Linear Layer,其他操作都是更高精度,比如 Weight 更新,Gradient 同步。因此,作者提出了優化的 FP8 混合精度 LLM 訓練策略。其主要包含 3 個方面的優化:FP8 通信,FP8 優化器,以及 FP8 分布式并行訓練。
9.2.1 FP8 梯度和 AllReduce 通信
作者發現直接使用 FP8 梯度進行梯度聚合會導致精度降低,這主要是因為低 bit 梯度聚合時有兩種 Scaling 機制 pre-scaling 和 post-scaling,容易出現 Underflow 和 Overflow 的問題。
如下圖所示為 pre-scaling 方案,假設有 N 個 GPU,則在求和之前先分別除以 N,此時容易出現 Underflow 的問題:
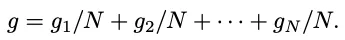
如下圖所示為 post-scaling,其主要區別是在求和之后再除以 N,然而此時又容易出現 Overflow 的問題:
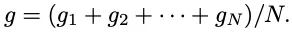
為了解決上述問題,作者提出了自定義的 FP8 梯度及 AllReduce 通信方案。由于其中介紹的比較晦澀,有些內容可能需要結合代碼才能說明白,比如其 auto scaling factor μ 和 scaling factor s 的關系以及計算方式,因此我們留作后續介紹。
9.2.2 FP8 優化器
在使用混合精度訓練時,如下圖所示,每個參數通常要對應 16 個字節,包括 FP32 的 Weight,Gradient 以及兩個 Adam 優化器狀態:
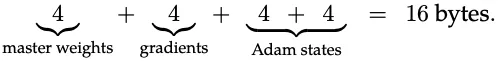
本文中,如下圖所示,作者直接使用 FP16 存儲 Weight,FP8 存儲 Gradient,兩個 Adam 優化器狀態一個是 FP8 一個是 FP 16,如此可將顯存占用降低 16/6=2.6x:
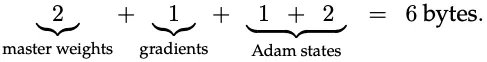
9.2.3 FP8 分布式并行訓練
這一部分的優化主要包含兩個方面:一個是 TP(Tensor Parallelism)適配 FP8,另一個是 ZeRO(Zero Redundancy Optimizer)適配 FP8。
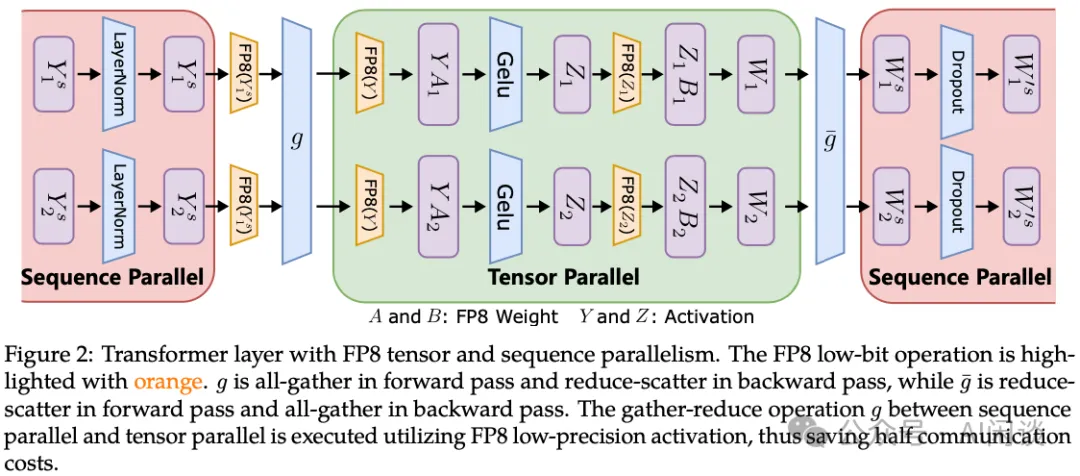
如下圖 Figure 2 所示為 TP 適配 FP8,其中的序列并行(Sequence Parallel)還是使用 FP16,然后在進行 TP 之前會轉換為 FP8 以降低通信量。之后 TP 中的 Linear 計算都使用 FP8(算力是 FP16 的 2 倍)。這樣可以同時實現降低通信量和提升計算效率的目的:
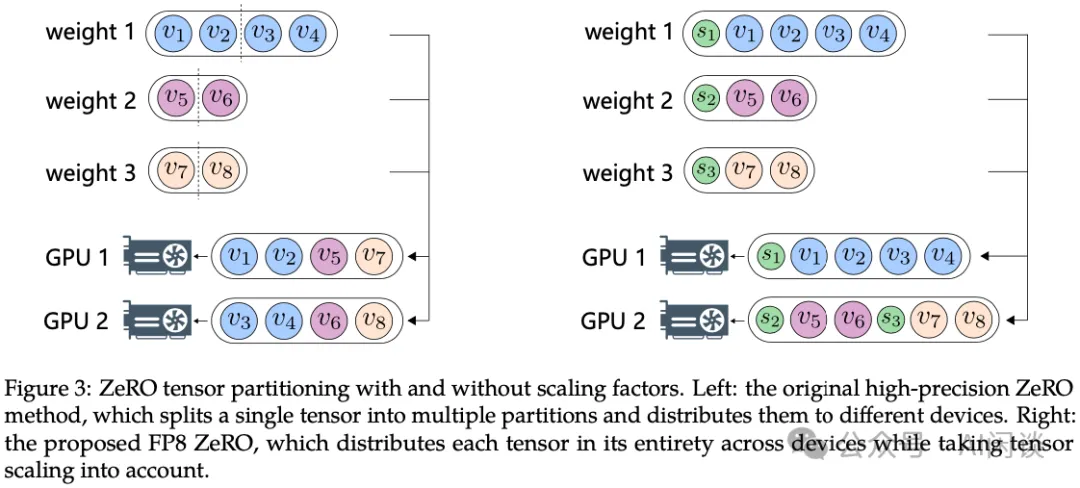
如下圖 Figure 3 所示為 ZeRO 適配 FP8,ZeRO 的核心就是實現模型狀態(Weight、Activation、Gradient)在不同 GPU 上的切分。如左圖所示,ZeRO 通常是直接按照 Tensor 均勻切分,每個 GPU 都有每個 Tensor 的一部分,這會導致 FP8 的 Scaling 操作需要考慮分布式場景,變得比較復雜;因此,作者采用了如右圖所示的方案,1 個 Tensor 只會在 1 個 GPU 上(也包含對應的 Scaling 值),可以采用貪心進行相對均勻的劃分,這種方式可以減少通信量和計算的復雜度。
9.3 實驗
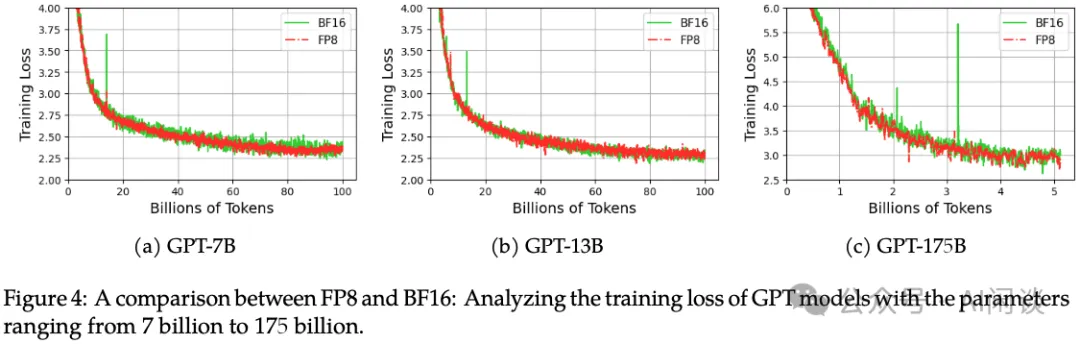
如下圖 Figure 4 所示,使用 FP8 和 BF16 分別訓練 GPT-7B、GPT-13B 和 GPT-175B 模型,其 Loss 基本都能對齊:
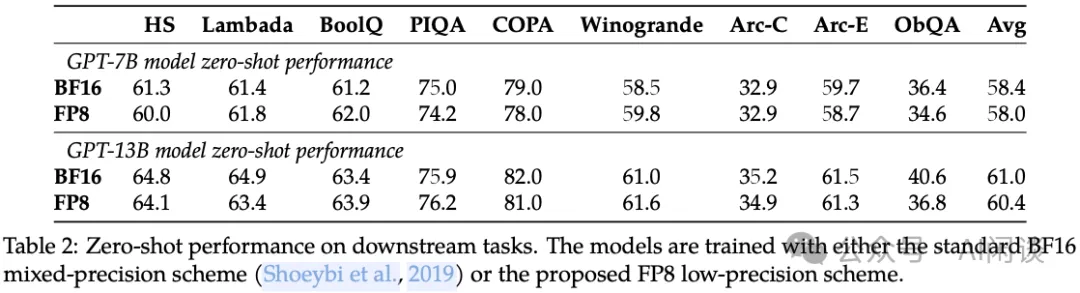
如下圖 Table 2 所示為在各種下游任務的 Zero-shot 表現,可以看出其平均精度也基本一致:
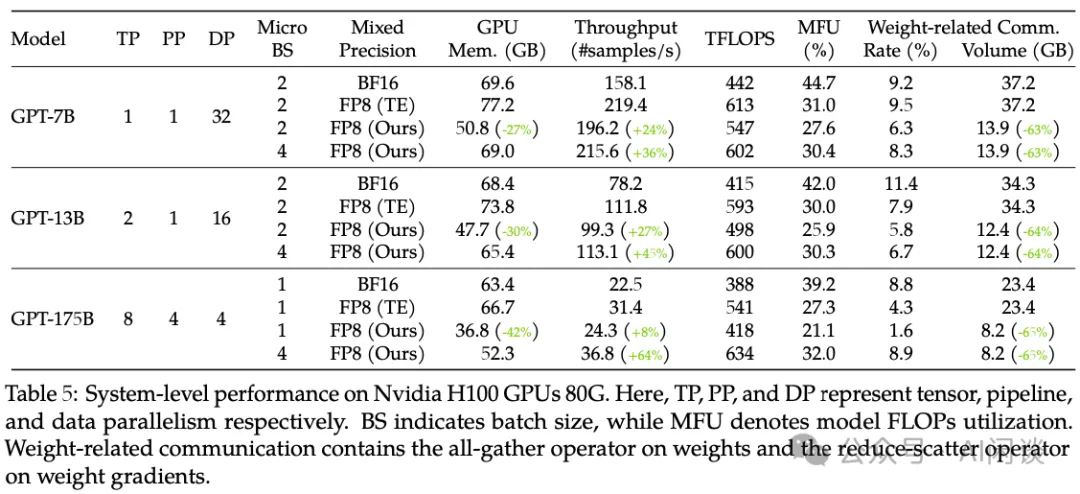
如下圖 Table 5 所示,作者也進一步對比了其性能表現,可以看出,提出的 FP8 訓練方案可以有效降低顯存使用并提升吞吐,在 175B 模型上最多可以提升 64% 的吞吐:
十、TensorRT-LLM & vLLM FP8
10.1 TensorRT-LLM
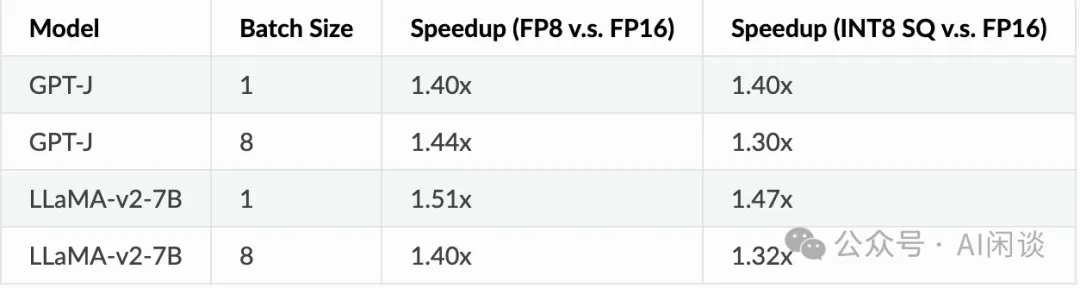
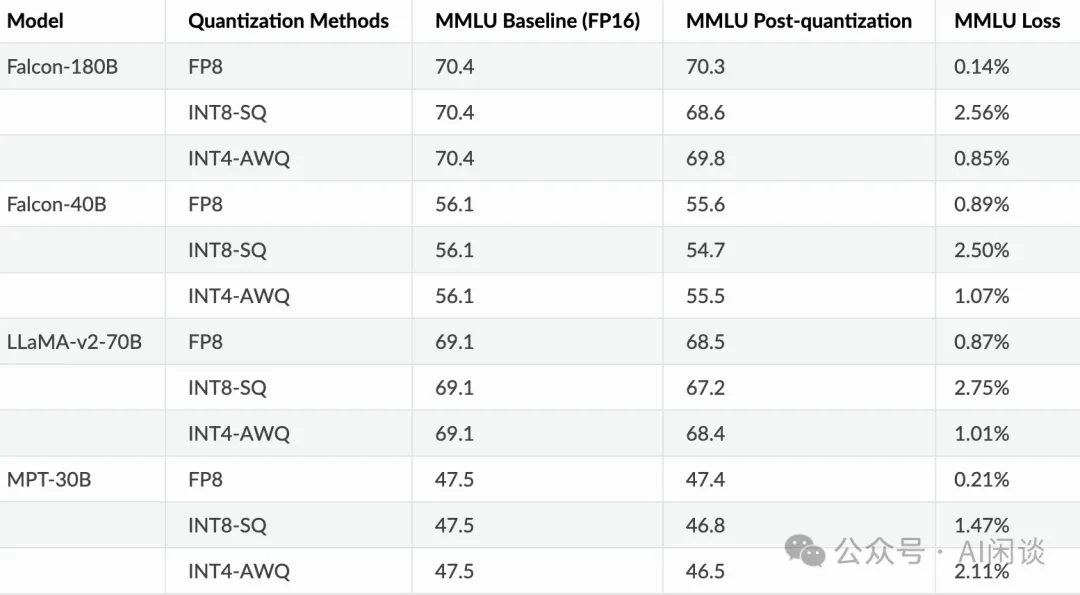
TensorRT-LLM 很早已經開始對 FP8 的支持,如下圖所示,其可以在速度和精度方面比 SmoothQuant 和 AWQ 有比較明顯的優勢。如果考慮 FP8 節約的顯存有助于使用更大的 Batch Size,FP8 甚至會比 FP16 獲得 2x 的吞吐提升(可參考 H100 has 4.6x A100 Performance in TensorRT-LLM, achieving 10,000 tok/s at 100ms to first token):
10.2 vLLM
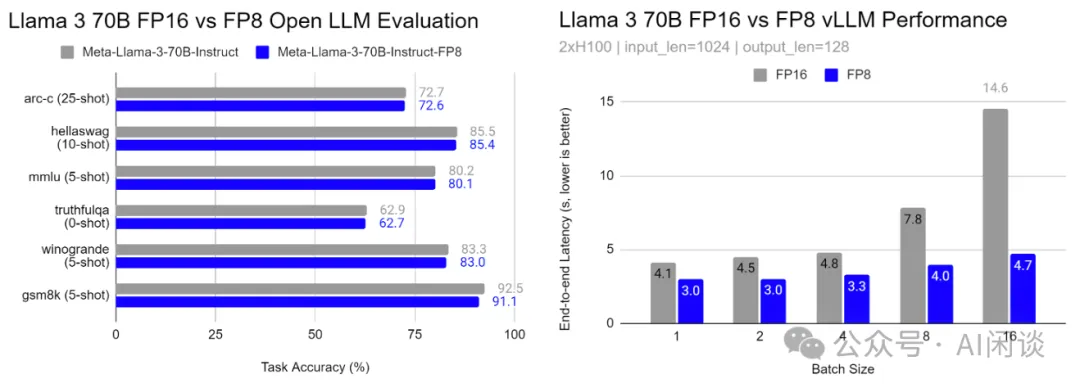
在 GitHub - neuralmagic/AutoFP8 中,也有用戶對 vLLM 的 FP8 推理進行了相應評估,可以看出,基于 Open LLM Evaluation 的評估表明 FP8 對精度的影響很小,對速度也能有比較大的提升:
十一、參考鏈接
- ??https://developer.nvidia.com/zh-cn/blog/nvidia-gpu-fp8-training-inference/??
- ??https://arxiv.org/abs/2310.18313??
- ??https://docs.nvidia.com/deeplearning/transformer-engine/user-guide/examples/fp8_primer.html??
- ??https://pytorch.org/docs/2.3/tensors.html??
- ??https://github.com/pytorch/pytorch/issues/107256??
- ??https://github.com/Dao-AILab/flash-attention??
- ??https://arxiv.org/abs/1812.08011??
- ??https://siboehm.com/articles/22/CUDA-MMM??
- ??https://proceedings.neurips.cc/paper_files/paper/2019/file/65fc9fb4897a89789352e211ca2d398f-Paper.pdf??
- ??https://arxiv.org/abs/2209.05433??
- ??https://arxiv.org/abs/2208.09225??
- ??https://arxiv.org/abs/2303.17951??
- ??https://arxiv.org/abs/2302.08007??
- ??https://arxiv.org/abs/2309.17224??
- ??https://arxiv.org/abs/2310.18313??
- ??https://github.com/Azure/MS-AMP??
- ??https://nvidia.github.io/TensorRT-LLM/blogs/H100vsA100.html??
- ??https://github.com/neuralmagic/AutoFP8??
本文轉載自 ??AI閑談??,作者: AI閑談

















