LLM架構從基礎到精通之門控循環單元(GRUs)
在之前對循環神經網絡(RNNs)和長短期記憶網絡(LSTMs)的深入探討中,我們了解了它們在處理序列數據方面的強大能力以及應對挑戰的獨特方式。接下來,我們將聚焦于另一種重要的神經網絡架構——門控循環單元(GRUs),它在解決標準 RNN 面臨的問題上展現出了獨特的優勢。
12. 門控循環單元(GRUs)
門控循環單元(GRU)由 Cho 等人在 2014 年提出,旨在解決標準循環神經網絡(RNN)面臨的梯度消失問題。GRU 與長短期記憶網絡(LSTM)有許多共同之處,這兩種算法都使用門控機制來控制記憶過程。
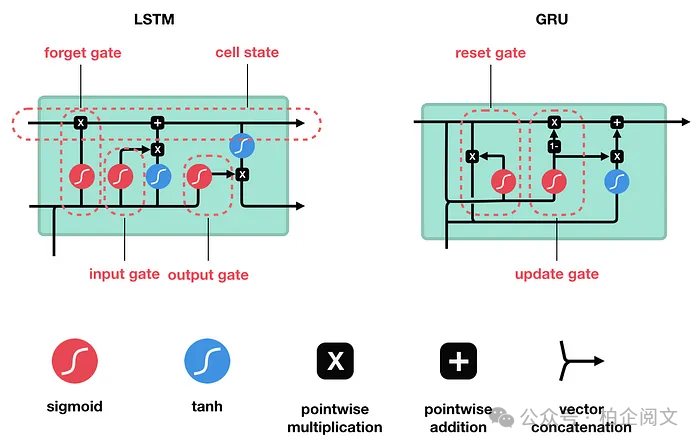
想象一下,你試圖通過反復聽一首歌來學習它。一個基本的 RNN 可能在聽到結尾時就忘記了歌曲的開頭。GRU 通過使用門來控制哪些信息被記住、哪些信息被遺忘,從而解決了這個問題。
GRU 通過將輸入門和遺忘門合并為一個單一的更新門,并添加一個重置門,簡化了長短期記憶網絡的結構。這使得它們訓練速度更快,使用更方便,同時仍然能夠長時間記住重要信息。
更新門:這個門決定了過去的信息中有多少應該被傳遞到未來。
重置門:這個門確定了過去的信息中有多少需要被忽略。
這些門幫助 GRU 在記住重要細節和忘記不重要的信息之間保持平衡,就像你在聽歌曲時可能會專注于記住旋律而忽略背景噪音一樣。
GRU 非常適合處理序列數據的任務,如預測股票市場、理解語言,甚至生成音樂。它們可以通過跟蹤過去的信息并利用這些信息進行更好的預測來學習數據中的模式。這使得它們在任何需要理解先前數據點上下文的應用中都非常有用。
12.1 與 LSTMs 和普通 RNNs 的比較
為了理解 GRU 的適用場景,讓我們將它們與 LSTMs 和普通 RNNs 進行比較。
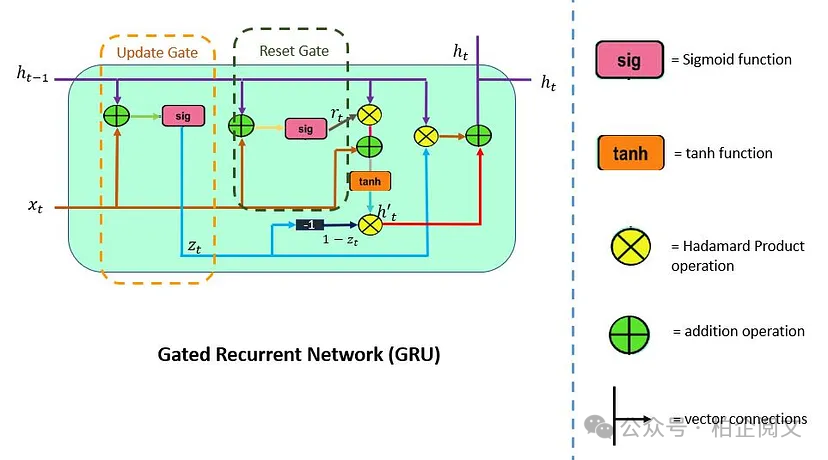
普通 RNNs:可以將普通 RNNs 視為循環神經網絡的基本版本。它們通過將信息從一個時間步傳遞到下一個時間步來工作,就像接力賽中每個賽跑者將接力棒傳遞給下一個人一樣。然而,它們有一個很大的缺陷:在長序列中它們往往會忘記信息。這是由于梯度消失問題,這使得它們難以學習數據中的長期依賴關系。
LSTMs:長短期記憶網絡旨在解決這個問題。它們使用更復雜的結構,包含三種類型的門:輸入門、遺忘門和輸出門。這些門就像一個復雜的文件系統,決定哪些信息要保留、哪些信息要更新、哪些信息要丟棄。這使得 LSTMs 能夠長時間記住重要信息,使它們非常適合處理需要跨多個時間步的上下文的任務,如理解文本段落或識別長時間序列中的模式。
GRUs:門控循環單元是 LSTMs 的簡化版本。它們通過將輸入門和遺忘門合并為一個單一的更新門,并添加一個重置門來簡化結構。這使得 GRUs 比 LSTMs 計算強度更低,訓練速度更快,同時仍然能夠有效地處理長期依賴關系。
12.2 是什么使 GRU 比傳統 RNN 更特殊和有效?
GRU 支持門控和隱藏狀態來控制信息的流動。為了解決 RNN 中出現的問題,GRU 使用兩個門:更新門和重置門。
你可以將它們視為兩個向量條目(0,1),可以執行凸組合。這些組合決定了哪些隱藏狀態信息應該被更新(傳遞)或在需要時重置隱藏狀態。同樣,網絡學會跳過不相關的臨時觀察。
LSTM 由三個門組成:輸入門、遺忘門和輸出門。與 LSTM 不同,GRU 沒有輸出門,并且將輸入門和遺忘門合并為一個單一的更新門。
接下來,讓我們更詳細地了解更新門和重置門。
12.2.1 更新門
更新門()負責確定需要傳遞到下一個狀態的先前信息(先前時間步)的數量。它是一個重要的單元。下面的示意圖展示了更新門的結構。
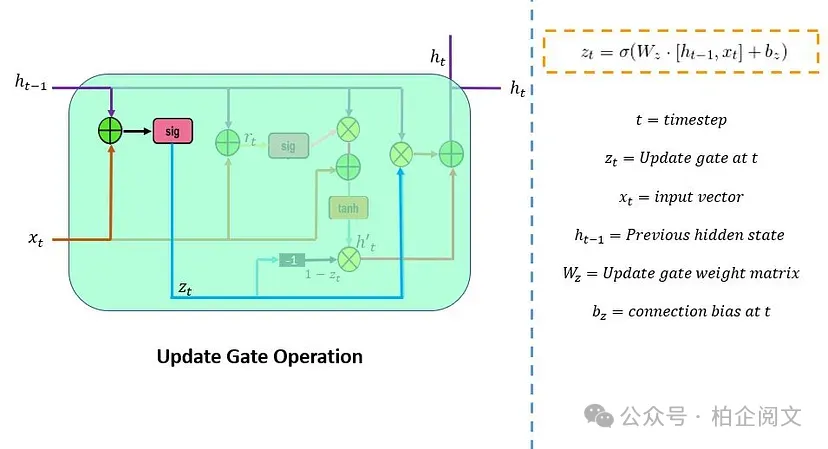
這里, 是網絡單元中的輸入向量,它與參數權重()矩陣相乘。 中的 表示它保存了前一個單元的信息,并與它的權重相乘。接下來,將這些參數的值相加,并通過 sigmoid 激活函數。在這里,sigmoid 函數將生成介于 0 和 1 之間的值。
12.2.2 重置門
重置門()用于決定需要忽略多少過去的信息。其公式與更新門相同,但它們的權重和門的使用方式有所不同。下面的示意圖表示了重置門。
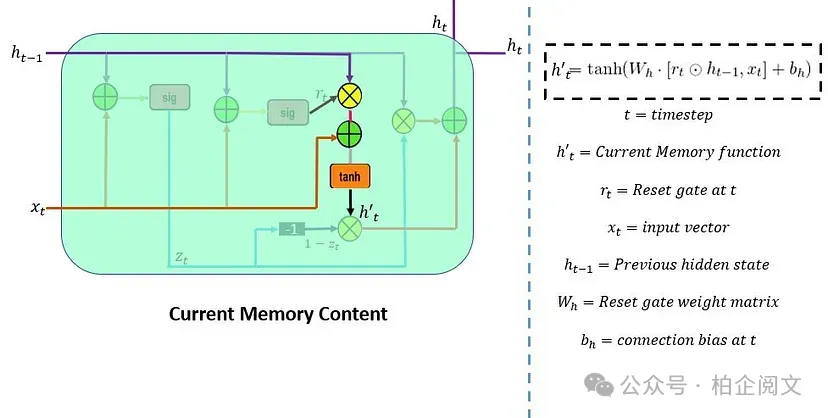
有兩個輸入, 和 。將它們與各自的權重相乘,進行逐點相加,并通過 sigmoid 函數。
13. 門的作用

14. 簡單 GRU 的實現
為了強化我們所涵蓋的概念,讓我們通過實踐,在 Python 中從頭開始實現一個基本的門控循環單元(GRU)。
下面的代碼片段展示了一個簡化的 GRU 類,突出了 GRU 架構中前向和后向傳播的基本功能。
import numpy as np
class SimpleGRU:
def __init__(self, input_size, hidden_size, output_size):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.W_z = np.random.randn(hidden_size, input_size)
self.U_z = np.random.randn(hidden_size, hidden_size)
self.b_z = np.zeros((hidden_size, 1))
self.W_r = np.random.randn(hidden_size, input_size)
self.U_r = np.random.randn(hidden_size, hidden_size)
self.b_r = np.zeros((hidden_size, 1))
self.W_h = np.random.randn(hidden_size, input_size)
self.U_h = np.random.randn(hidden_size, hidden_size)
self.b_h = np.zeros((hidden_size, 1))
self.W_y = np.random.randn(output_size, hidden_size)
self.b_y = np.zeros((output_size, 1))
def sigmoid(self, x):
return1 / (1 + np.exp(-x))
def tanh(self, x):
return np.tanh(x)
def softmax(self, x):
exp_x = np.exp(x - np.max(x))
return exp_x / exp_x.sum(axis=0, keepdims=True)
def forward(self, x):
T = len(x)
h = np.zeros((self.hidden_size, 1))
y_list = []
for t in range(T):
x_t = x[t].reshape(-1, 1)
z = self.sigmoid(np.dot(self.W_z, x_t) + np.dot(self.U_z, h) + self.b_z)
r = self.sigmoid(np.dot(self.W_r, x_t) + np.dot(self.U_r, h) + self.b_r)
h_tilde = self.tanh(np.dot(self.W_h, x_t) + np.dot(self.U_h, r * h) + self.b_h)
h = (1 - z) * h + z * h_tilde
y = np.dot(self.W_y, h) + self.b_y
y_list.append(y)
return y_list
def backward(self, x, y_list, target):
T = len(x)
dW_z = np.zeros_like(self.W_z)
dU_z = np.zeros_like(self.U_z)
db_z = np.zeros_like(self.b_z)
dW_r = np.zeros_like(self.W_r)
dU_r = np.zeros_like(self.U_r)
db_r = np.zeros_like(self.b_r)
dW_h = np.zeros_like(self.W_h)
dU_h = np.zeros_like(self.U_h)
db_h = np.zeros_like(self.b_h)
dW_y = np.zeros_like(self.W_y)
db_y = np.zeros_like(self.b_y)
dh_next = np.zeros_like(y_list[0])
for t in reversed(range(T)):
dy = y_list[t] - target[t]
dW_y += np.dot(dy, np.transpose(h))
db_y += dy
dh = np.dot(np.transpose(self.W_y), dy) + dh_next
dh_tilde = dh * (1 - self.sigmoid(np.dot(self.W_z, x[t].reshape(-1, 1)) + np.dot(self.U_z, h) + self.b_z))
dW_h += np.dot(dh_tilde, np.transpose(x[t].reshape(1, -1)))
db_h += dh_tilde
dr = np.dot(np.transpose(self.W_h), dh_tilde)
dU_h += np.dot(dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h)), np.transpose(h))
dW_h += np.dot(dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h)), np.transpose(x[t].respose(1, -1)))
db_h += dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h))
dz = np.dot(np.transpose(self.U_r), dr * h * (self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h) - h_tilde))
dU_z += np.dot(dz * h * z * (1 - z), np.transpose(h))
dW_z += np.dot(dz * h * z * (1 - z), np.transpose(x[t].reshape(1, -1)))
db_z += dz * h * z * (1 - z)
dh_next = np.dot(np.transpose(self.U_z), dz * h * z * (1 - z))
return dW_z, dU_z, db_z, dW_r, dU_r, db_r, dW_h, dU_h, db_h, dW_y, db_y
def update_parameters(self, dW_z, dU_z, db_z, dW_r, dU_r, db_r, dW_h, dU_h, db_h, dW_y, db_y, learning_rate):
self.W_z -= learning_rate * dW_z
self.U_z -= learning_rate * dU_z
self.b_z -= learning_rate * db_z
self.W_r -= learning_rate * dW_r
self.U_r -= learning_rate * dU_r
self.b_r -= learning_rate * db_r
self.W_h -= learning_rate * dW_h
self.U_h -= learning_rate * dU_h
self.b_h -= learning_rate * db_h
self.W_y -= learning_rate * dW_y
self.b_y -= learning_rate * db_y在上述實現中,我們引入了一個簡化的 ??SimpleGRU?? 類,以展示 GRU 的核心機制。示例用法演示了如何初始化 GRU、創建輸入序列和目標輸出的隨機數據、執行前向和后向傳播,以及隨后使用計算出的梯度更新權重和偏差。
14.1 GRUs 的優缺點
GRUs 的優點
- 序列數據建模:GRUs 在處理序列方面表現出色,非常適合語言處理、語音識別和時間序列分析等任務。
- 可變長度輸入:GRUs 可以處理不同長度的序列,適用于輸入大小不同的應用場景。
- 計算效率高:與更復雜的循環架構(如 LSTMs)相比,由于其更簡單的設計,GRUs 在計算上更高效。
- 緩解梯度消失:GRUs 比傳統 RNNs 更有效地解決了梯度消失問題,能夠捕獲數據中的長期依賴關系。
GRUs 的局限性
- 長期記憶有限:雖然 GRUs 在捕獲長期依賴關系方面比標準 RNNs 更好,但對于具有復雜依賴關系的非常長的序列,它們可能不如 LSTMs 有效。
- 表達能力較弱:在某些情況下,GRUs 可能無法像 LSTMs 那樣有效地捕獲復雜的模式,特別是在對高度復雜的序列進行建模時。
- 特定應用:對于需要顯式內存控制或復雜上下文建模的任務,LSTMs 或更高級的架構可能更合適。
14.2 在 GRUs 和 LSTMs 之間選擇
選擇使用門控循環單元(GRUs)還是長短期記憶(LSTM)網絡取決于你的具體問題和數據集。以下是一些考慮因素:
使用 GRUs 的情況:
- 計算資源有限:與 LSTMs 相比,GRUs 的計算強度較低,在資源受限的情況下是首選。
- 簡單性重要:如果你想要一個更簡單的模型,同時仍然能夠合理地捕獲序列依賴關系,GRUs 是一個不錯的選擇。
- 較短序列:對于涉及較短依賴關系的序列任務,GRUs 可以提供足夠的性能,而無需 LSTM 的復雜內存管理。
使用 LSTMs 的情況:
- 捕獲長期依賴關系:LSTMs 更適合于捕獲長程依賴關系至關重要的任務,如語言建模、語音識別和某些時間序列預測。
- 精細的內存控制:LSTMs 提供了對內存的更明確控制,在需要精確內存處理時是更好的選擇。
- 復雜序列:如果你的數據呈現出復雜的序列模式和依賴關系,LSTMs 通常在建模這些復雜性方面更有效。
在實踐中,最好在你的特定任務上對 GRUs 和 LSTMs 進行實驗,以確定哪種架構性能更好。有時,兩者之間的選擇取決于對數據集的實證測試和驗證。
15. 結論
我們深入探討了循環神經網絡(RNNs),詳細研究了它們的核心機制、訓練挑戰以及提高性能的高級設計。以下是一個簡要概述:
我們剖析了 RNNs 的結構,強調了它們通過內部記憶狀態處理序列的能力。討論了關鍵過程,如前向傳播和時間反向傳播(BPTT),解釋了 RNNs 如何處理序列數據。
我們還強調了主要的訓練挑戰,包括梯度消失和爆炸,這些問題可能會干擾學習。為了解決這些問題,我們探索了諸如梯度裁剪和初始化策略等解決方案,這些方案有助于穩定訓練并提高網絡從較長序列中學習的能力。
門控循環單元(GRUs)是 RNNs 的一種強大變體,專為高效處理序列數據而設計。它們有效地緩解了梯度消失等問題,并擅長捕獲序列中的依賴關系,使其非常適合自然語言處理、語音識別和時間序列分析等任務。
GRUs 使用門控機制來控制信息的流動,使其能夠在保持計算效率的同時捕獲長期依賴關系。理解 GRUs 背后的架構和數學原理是在機器學習任務中有效利用它們的關鍵。
在選擇 GRUs 和 LSTMs 時,需要考慮多個因素,包括數據復雜性、計算資源和要建模的依賴關系的長度。這兩種架構都有其優缺點,因此最佳選擇取決于任務的具體要求。
本文轉載自 ??柏企閱文??,作者: 柏企

















