大牛推薦:iOS 自定義下拉線條動(dòng)畫
這是本章的第二個(gè) demo,下面這個(gè)案例中,我把線條動(dòng)畫和數(shù)學(xué)知識(shí)結(jié)合在了一起。通過(guò)這個(gè)案例,可以很好地向你展示如何自己歸納出一個(gè)數(shù)學(xué)公式,并把它用到一個(gè)自定義動(dòng)畫中。
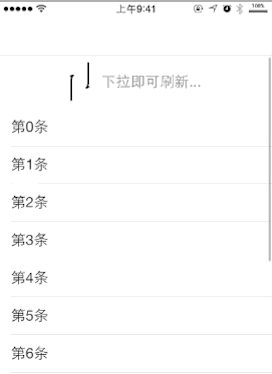
首先,我們還是先看最終效果 :
OK,可以看到隨著手指在屏幕上滑動(dòng)距離的改變,線條一開始逐漸靠攏,到達(dá)一定位置后開始彎曲,最終合并成了一個(gè)圓。順便一提,我已經(jīng)把這個(gè)動(dòng)畫封裝到了一個(gè)上拉、下拉刷新的控件中,并且用在了大象公會(huì)這款獨(dú)立開發(fā)的 App 中。 你可以提前下載下來(lái)一睹實(shí)際效果。
下面講講我是怎么思考這個(gè)動(dòng)畫的。首先,最終控制這個(gè)動(dòng)畫進(jìn)度的是一個(gè) CALayer 內(nèi)部的自定義的屬性:
- @property(nonatomic,assign)CGFloat progress;
無(wú)論你是通過(guò)手指滑動(dòng)產(chǎn)生偏移量,還是滑動(dòng) UISlider 改變一個(gè)數(shù)值,最終都將轉(zhuǎn)化到這個(gè)屬性的改變。然后,在這個(gè)屬性的 setter 方法里,我們讓 layer 去實(shí)時(shí)地重繪,就像這樣:
- -(void)setProgress:(CGFloat)progress{ self.curveLayer.progress = progress;
- [self.curveLayer setNeedsDisplay];
- }
至于重繪的算法,屬于細(xì)節(jié)上要考慮的事了。我們做一個(gè)動(dòng)畫的步驟都是先考慮宏觀,再去考慮細(xì)節(jié)上的實(shí)現(xiàn)。就像開發(fā)一個(gè) App 一樣,一開始肯定是先考慮架構(gòu),再去往這個(gè)框架里添磚加瓦,修修補(bǔ)補(bǔ)。現(xiàn)在,我們對(duì)這個(gè)動(dòng)畫的整體思路已經(jīng)清楚了,下面開始深入到細(xì)節(jié)去思考具體算法的實(shí)現(xiàn)。我把這個(gè)動(dòng)畫分成了兩個(gè)階段:0~0.5 和 0.5~1.0。 這是什么意思?
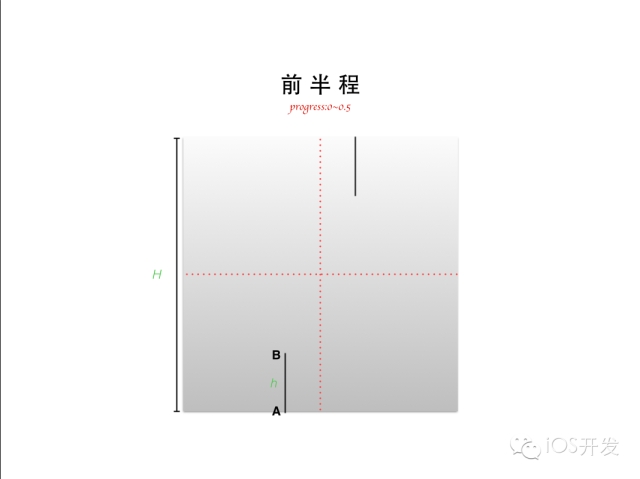
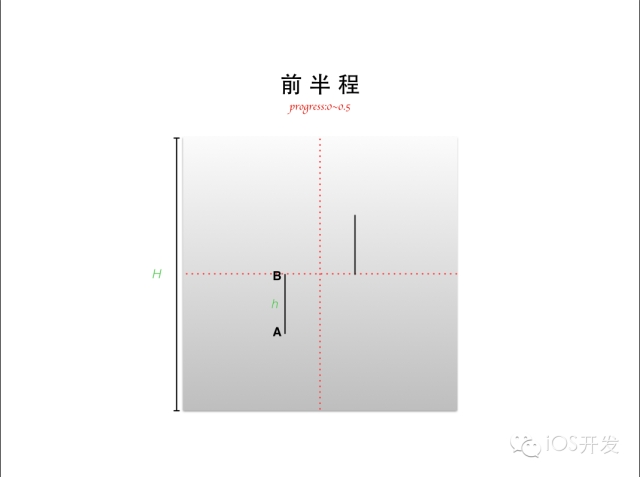
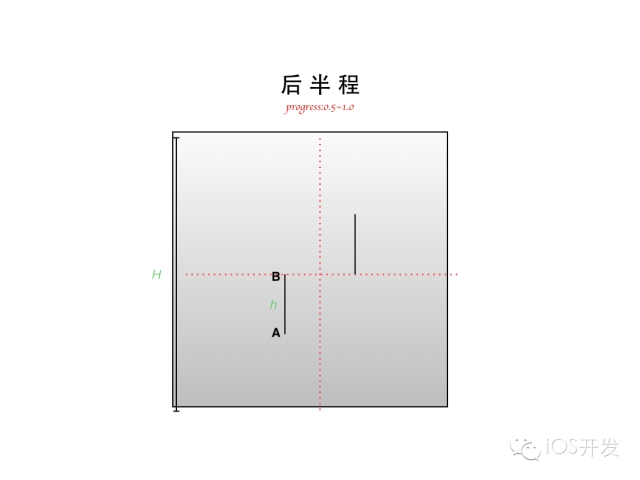
做動(dòng)畫還是那句話 ——「善于分解」。我們先看前半程,也就是 progress 從一開始的 0 運(yùn)動(dòng)到中間狀態(tài) 0.5 的這一個(gè)階段。這一個(gè)階段兩條線段分別從上方和下方兩個(gè)方向向中間運(yùn)動(dòng),直到接觸到中線為止。這一階段的畫線算法非常簡(jiǎn)單,只要能實(shí)時(shí)獲得 A,B 兩點(diǎn)的坐標(biāo),剩下用 UIBezierPath 的 moveToPoint,addLineToPoint 就完事了。所以,問(wèn)題轉(zhuǎn)換成了求 A,B 兩點(diǎn)運(yùn)動(dòng)的公式(其實(shí)只要求出一點(diǎn),另一點(diǎn)無(wú)非就相差了一個(gè)線段長(zhǎng)度 h)。請(qǐng)看演示動(dòng)畫(注:在電子書中是有交互動(dòng)畫的,但因?yàn)楝F(xiàn)在是以文章的形式呈現(xiàn),所以我只能通過(guò)圖片的方式向你展示)
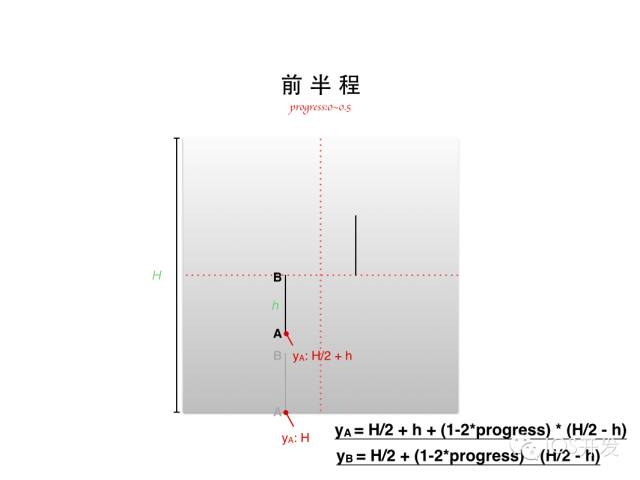
其實(shí)你只要愿意動(dòng)筆在紙上嘗試推演一番,并不難求得這兩個(gè)點(diǎn)的運(yùn)動(dòng)公式:
yA = H/2 + h + (1-2progress) (H/2 - h)
yB = H/2 + (1-2progress) (H/2 - h)
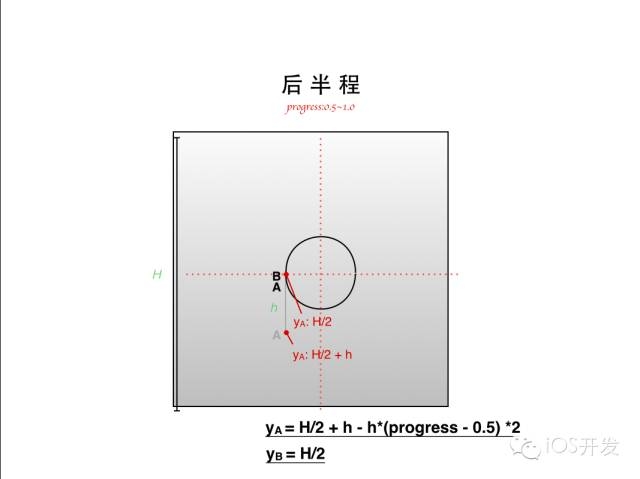
接下來(lái)是動(dòng)畫的第二階段 0.5~1.0。這個(gè)階段有些許復(fù)雜:「B 點(diǎn)保持不動(dòng),A 點(diǎn)繼續(xù)運(yùn)動(dòng)到 B 的位置,同時(shí),在頂部根據(jù)當(dāng)前的進(jìn)度再畫出圓弧」。視覺上給人的感覺就好像尾巴在逐漸縮短,頭部在慢慢彎曲。同樣的,我只能以圖片的形式向你展示。
在這個(gè)過(guò)程中,我們不難先求得 A 點(diǎn)的坐標(biāo)是:
yA = H/2 + h - h(progress - 0.5) 2
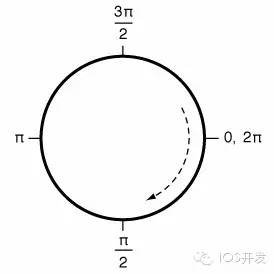
比較麻煩的是這個(gè)圓弧該怎么畫?答案是可以用 UIBezierPath 中提供的 - (void)addArcWithCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise NS_AVAILABLE_IOS(4_0); 這個(gè)方法繪制出圓弧。具體思路是:以 CGPointMake(self.frame.size.width/2,self.frame.size.height/2) 為圓心,10 為半徑,按順時(shí)針?lè)较颍瑥?M_PI(90°) 的起始角度,畫到 2*M_PI 的結(jié)束角度。
關(guān)于 - (void)addArcWithCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise; 方法的解釋:如果設(shè)置開始角度均為 0 ,結(jié)束角度均為 π。那么設(shè)置 clockwise(順時(shí)針) 為 YES 時(shí),畫出的是下半段圓弧;反之, 設(shè)置 clockwise(順時(shí)針) 為 NO 時(shí),畫出的是上半段圓弧;
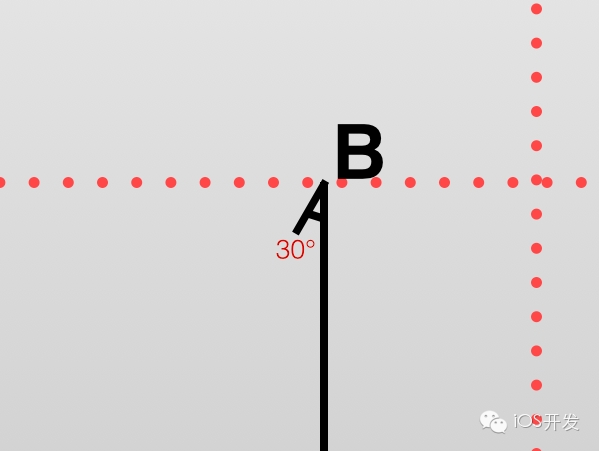
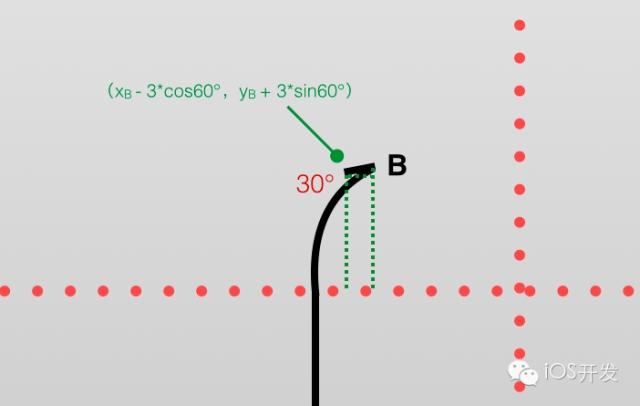
以上,我們只完成了一條線段的整個(gè)過(guò)程。同理,也能獲得另一條線段的繪制算法。最后,別忘了線段頂端還有個(gè)箭頭。繪制箭頭的算法 Gallery 4.1:我們以 B 點(diǎn)作為箭頭的起始起點(diǎn),斜向左下方 30° 角延長(zhǎng) 3 個(gè)單位。彎曲之后也同理,只需要額外加上線段轉(zhuǎn)過(guò)的角度即可。
相應(yīng)的代碼就是:
- [arrowPath moveToPoint:pointB];
- [arrowPath addLineToPoint:CGPointMake(pointB.x - 3*(cosf(Degree)), pointB.y + 3*(sinf(Degree)))];
- [curvePath1 appendPath:arrowPath];
OK,這一個(gè) demo 的分析到這里就結(jié)束了。完整代碼可以在本書對(duì)應(yīng)的 Github Repo:https://github.com/KittenYang/A-GUIDE-TO-iOS-ANIMATION 中下載。
關(guān)于作者:KITTEN-YANG,大四在讀,目前在錘子科技做 iOS 實(shí)習(xí)。平時(shí)癡迷于交互動(dòng)畫,立志做一名頂尖的軟件工程師兼交互設(shè)計(jì)師。您可以參觀我的個(gè)人網(wǎng)站 http://kittenyang.com 或者來(lái)我的微博交個(gè)朋友:@KITTEN-YANG 謝謝。