[[172547]]

大家好，我是FlappyPig的隊長bibi，近期因為一些比賽以及其他原因，總結(jié)了一些RSA方面的東西，于是在這里與大家分享，希望大家能有所收獲，如有不當之處敬請批評指正。

0x01 前言

這里就不討論數(shù)論的基礎(chǔ)了，進行RSA的題目解答，至少要懂得基本的數(shù)論知識的，如果不了解數(shù)論的基本知識的話，網(wǎng)上相關(guān)內(nèi)容還是挺多的。

RSA基于一個簡單的數(shù)論事實，兩個大素數(shù)相乘十分容易，將其進行因式分解確實困難的。在量子計算機還沒有成熟的今天，RSA算法憑借其良好的抵抗各種攻擊的能力，在公鑰密碼體制中發(fā)揮著中流砥柱的作用。然而即便RSA算法目前來說是安全可靠的，但是錯誤的應(yīng)用場景，錯誤的環(huán)境配置，以及錯誤的使用方法，都會導(dǎo)致RSA的算法體系出現(xiàn)問題，從而也派生出針對各種特定場景下的RSA攻擊方法。

本文針對一些在CTF中常見的RSA攻擊方法，從如何識別應(yīng)該應(yīng)用那種方法以及如何去解題來介紹CTF中的RSA題目的常見解法。

RSA算法描述

RSA算法涉及三個參數(shù)，n，e，d，私鑰為n，d，公鑰為n，e。

其中n是兩個大素數(shù)p，q的乘積。

d是e模φ(n)'>φ(n)φ(n)的逆元，φ(n)'>φ(n)φ(n)是n的歐拉函數(shù)。

c為密文，m為明文，則加密過程如下：

c≡memodn'>c≡memodnc≡memodn 

解密過程如下：

m≡cd'>m≡cdm≡cd mod'>modmod n'>nn 

n，e是公開的情況下，想要知道d的值，必須要將n分解計算出n的歐拉函數(shù)值，而n是兩個大素數(shù)p，q的乘積，將其分解是困難的。

RSA題目類型

在CTF競賽中，RSA理所當然處在CRYPTO中居多。而且RSA作為典型的加密算法，其出鏡率可謂相當高，基本上所有比賽都會有幾道RSA的題目出現(xiàn)。

數(shù)據(jù)處理

在進行做題之前，我們要將數(shù)據(jù)處理成可以做題的模式。基本上來說，RSA的題目都是圍繞著c，m，e，d，n，p，q這幾個參數(shù)展開的，但是題目一般不會直接給這種樣子的參數(shù)，而是通過別的方式給出，這里就需要我們使用一些工具或者自己手工將這些參數(shù)提取出來。

pem文件：針對此類文件可以直接使用openssl提取，大概使用過的方式有：

openssl rsautl -encrypt -in FLAG -inkey public.pem -pubin -out flag.enc  
openssl rsa -pubin -text -modulus -in warmup -in public.pem 

pcap文件：針對此類文件可以使用wireshark follow一下。這種問題一般都是寫了一個交互的crypto系統(tǒng)，所以可能產(chǎn)生多輪交互。

PPC模式：這種模式是上述pcap文件的交互版，會給一個端口進行一些crypto的交互，參數(shù)會在交互中給出。

第二個需要處理的就是明密文，這個方法多多，不多贅述。

0x02 模數(shù)分解

說一說

解決RSA題目最簡單，最暴力，最好使的方法就是分解模數(shù)n。如果能夠?qū)分解成功，成功得到p，q的取值，那么可求n的歐拉函數(shù)的值。

φ(n)=(p−1)(q−1)'>φ(n)=(p−1)(q−1)φ(n)=(p−1)(q−1) 

而通過e，d與n的歐拉函數(shù)滿足如下關(guān)系：

ed=1'>ed=1ed=1 mod'>modmod φ(n)'>φ(n)φ(n) 

通過歐幾里得算法可以通過e與n的歐拉函數(shù)的值輕易求出d，從而計算出解密密鑰。

即在知道e，p，q的情況下，可以解出d：

def egcd(a, b):  
if a == 0:  
return (b, 0, 1)  
else:  
g, y, x = egcd(b % a, a)  
return (g, x - (b // a) * y, y)  
def modinv(a, m):  
g, x, y = egcd(a, m)  
if g != 1:  
raise Exception('modular inverse does not exist')  
else:  
return x % m 

modinv函數(shù)即為求模擬的函數(shù)，在知道e，p，q的情況下，可以：

d=modinv(e,(p-1)*(q-1)) 

即可求出解密密鑰。

寫到這里，要提出一個細節(jié)問題，在利用python進行rsa的題目求解過程中：

c≡memodn'>c≡memodnc≡memodn 

此類運算需要使用pow函數(shù)來進行求解，而不是直接m**e % n，這樣會慢死的。Python在處理此類運算進行了優(yōu)化。比如剛才在已知p，q的時候利用modinv函數(shù)求出了d，然后就可以利用pow函數(shù)求出明文：

m=pow(c,d,n) 

例題：

https://www.jarvisoj.com (very easy RSA) 

題目中直接給了p，q，e。

可以直接求出d：

p = 3487583947589437589237958723892346254777  
q = 8767867843568934765983476584376578389  
e = 65537  
d = modinv(e, (p-1)*(q-1))  
print d 

直接分解n

介紹：

素數(shù)分解問題是困難的，但是可以通過計算機進行暴力分解。1999年，名為Cray的超級計算機用了5個月時間分解了512bit的n。2009年，一群研究人員成功分解了768bit的n。2010年，又提出了一些針對1024bit的n的分解的途徑，但是沒有正面分解成功。通常意義上來說，一般認為2048bit以上的n是安全的。現(xiàn)在一般的公鑰證書都是4096bit的證書。

如果n比較小，那么可以通過工具進行直接n分解，從而得到私鑰。如果n的大小小于256bit，那么我們通過本地工具即可爆破成功。例如采用windows平臺的RSATool2v17，可以在幾分鐘內(nèi)完成256bit的n的分解。

如果n在768bit或者更高，可以嘗試使用一些在線的n分解網(wǎng)站，這些網(wǎng)站會存儲一些已經(jīng)分解成功的n，比如：http://factordb.com

通過在此類網(wǎng)站上查詢n，如果可以分解或者之前分解成功過，那么可以直接得到p和q。然后利用前述方法求解得到密文。

識別：

此類問題一般是分值較小的題目，提取出n之后可以發(fā)現(xiàn)n的長度小于等于512bit，可以直接取分解n。如果大于512bit，建議在使用每個題目都用后面所說的方法去解題。

{C} 例題：

比如在某次競賽中，發(fā)現(xiàn)：

n=87924348264132406875276140514499937145050893665602592992418171647042491658461 

利用factordb分解：

 

利用公約數(shù)

介紹：

如果在兩次公鑰的加密過程中使用的n1'>n1n1 和n2'>n2n2具有相同的素因子，那么可以利用歐幾里得算法直接將n1'>n1n1和n2'>n2n2分解。

通過歐幾里得算法可以直接求出n1'>n1n1和n2'>n2n2的最大公約數(shù)p：

(n1,n2)=p'>(n1,n2)=p(n1,n2)=p 

可以得出：

n1=p'>n1=pn1=pq1'>q1q1  
n2=p'>n2=pn2=pq2'>q2q2 

直接分解成功。而歐幾里得算法的時間復(fù)雜度為：O(log n)。這個時間復(fù)雜度即便是4096 bit也是秒破級別。

def gcd(a, b):  
if a  
a, b = b, a  
while b != 0:  
temp = a % b  
a = b  
b = temp  
return a 

識別此類題目，通常會發(fā)現(xiàn)題目給了若干個n，均不相同，并且都是2048bit，4096bit級別，無法正面硬杠，并且明文都沒什么聯(lián)系，e也一般取65537。 識別：

例題：

在一個題目中，你拿到了兩個n，e都為65537，兩個n分別為：

n1=9051013965404084482870087864821455535159008696042953021965631089095795348830954383127323853272528967729311045179605407693592665683311660581204886571146327720288455874927281128121117323579691204792399913106627543274457036172455814805715668293705603675386878220947722186914112990452722174363713630297685159669328951520891938403452797650685849523658191947411429068829734053745180460758604283051344339641429819373112365211739216160420494167071996438506850526168389386850499796102003625404245645796271690310748804327 
n2=13225948396179603816062046418717214792668512413625091569997524364243995991961018894150059207824093837420451375240550310050209398964506318518991620142575926623780411532257230701985821629425722030608722035570690474171259238153947095310303522831971664666067542649034461621725656234869005501293423975184701929729170077280251436216167293058560030089006140224375425679571181787206982712477261432579537981278055755344573767076951793312062480275004564657590263719816033564139497109942073701755011873153205366238585665743 

通過直接分解，上factordb都分解失敗。通過嘗試發(fā)現(xiàn)：

print gcd(n1,n2) 

打印出：

1564859779720039565508870182569324208117555667917997801104862601098933699462849007879184203051278194180664616470669559575370868384820368930104560074538872199213236203822337186927275879139590248731148622362880471439310489228147093224418374555428793546002109

則此致即為兩個n共有的素因子p，然后進一步求出q，求解完畢。

Fermat方法與Pollard rho方法

介紹：

針對大整數(shù)的分解有很多種算法，性能上各有優(yōu)異，有Fermat方法，Pollard rho方法，試除法，以及橢圓曲線法，連分數(shù)法，二次篩選法，數(shù)域分析法等等。其中一些方法應(yīng)用在RSA的攻擊上也有奇效。

在p，q的取值差異過大，或者p，q的取值過于相近的時候，F(xiàn)ormat方法與Pollard rho方法都可以很快將n分解成功。

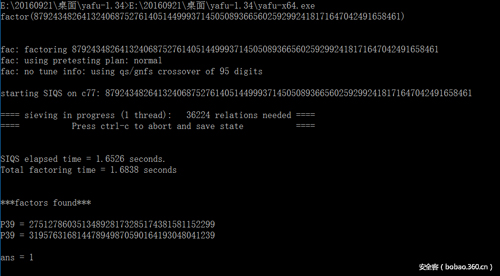
此類分解方法有一個開源項目yafu將其自動化實現(xiàn)了，不論n的大小，只要p和q存在相差過大或者過近時，都可以通過yafu很快地分解成功。

識別：

在直接分解n無望，不能利用公約數(shù)分解n之后，都應(yīng)該使用yafu去試一下。

例題：

https://www.jarvisoj.com (Medium RSA)

此題首先從pem中提取N和e，然后上yafu，直接分解成功。

想掙錢?什么工作可以年薪30萬?【點擊進入】想拿高薪?想變身高富帥?變身白富美?那就來 華信智原學(xué)Java,大牛導(dǎo)師帶你走向人生巔峰!查 看

0x03 低加密指數(shù)攻擊

在RSA中e也稱為加密指數(shù)。由于e是可以隨意選取的，選取小一點的e可以縮短加密時間，但是選取不當?shù)脑挘蜁斐砂踩珕栴}。

e=3時的小明文攻擊

介紹：

當e=3時，如果明文過小，導(dǎo)致明文的三次方仍然小于n，那么通過直接對密文三次開方，即可得到明文。

即：

c≡me'>c≡mec≡me mod'>modmod n'>nn 

如果e=3，且men'>menmen，那么：

c=me,'>c=me,c=me, e=3'>e=3e=3  
m=c3'>m=3√cm=c3 

如果明文的三次方比n大，但是不是足夠大，那么設(shè)k，有：

c=me+kn'>c=me+knc=me+kn 

爆破k，如果c−kn'>c−knc−kn能開三次根式，那么可以直接得到明文。

識別：

推薦在e=3的時候首先嘗試這種方法。

例題：

https://www.jarvisoj.com (Extremely hard RSA)

關(guān)鍵代碼如下：此題通過不斷給明文+n開三次方即可求得：

i=0  
while 1:  
if(gmpy.root(c+i*N, 3)[1]==1):  
print gmpy.root(c+i*N, 3)  
break  
i=i+1 

低加密指數(shù)廣播攻擊

介紹：

如果選取的加密指數(shù)較低，并且使用了相同的加密指數(shù)給一個接受者的群發(fā)送相同的信息，那么可以進行廣播攻擊得到明文。

即，選取了相同的加密指數(shù)e(這里取e=3)，對相同的明文m進行了加密并進行了消息的傳遞，那么有：

c1≡me'>c1≡mec1≡me mod'>modmod n1'>n1n1  
c2≡me'>c2≡mec2≡me mod'>modmod n2'>n2n2  
c3≡me'>c3≡mec3≡me mod'>modmod n3'>n3n3 

對上述等式運用中國剩余定理，在e=3時，可以得到：

cx≡m3'>cx≡m3cx≡m3 mod'>modmod n1n2n3'>n1n2n3n1n2n3 

通過對cx'>cxcx進行三次開方可以求得明文。

識別：

這個識別起來比較簡單，一般來說都是給了三組加密的參數(shù)和明密文，其中題目很明確地能告訴你這三組的明文都是一樣的，并且e都取了一個較小的數(shù)字。

例題：

SCTF2016，CODE300

題目第二輪中通過流量包的方式給了廣播攻擊的參數(shù)。

這里我就不賣萌了，直接給國外類似一題的網(wǎng)址：http://codezen.fr/2014/01/16/hackyou-2014-crypto-400-cryptonet

Coppersmith定理攻擊

Coppersmith定理指出在一個e階的mod n多項式f(x)中，如果有一個根小于n1e'>n1en1e，就可以運用一個O(log n)的算法求出這些根。

這個定理可以應(yīng)用于RSA算法。如果e = 3并且在明文當中只有三分之二的比特是已知的，這種算法可以求出明文中所有的比特。

并未找到真題。

0x04 低解密指數(shù)攻擊

介紹：

與低加密指數(shù)相同，低解密指數(shù)可以加快解密的過程，但是者也帶來了安全問題。Wiener表示如果滿足：

d13gn14'>d13gn14d13gn14 

那么一種基于連分數(shù)(一個數(shù)論當中的問題)的特殊攻擊類型就可以危害RSA的安全。此時需要滿足：

q'>qqp'>pp2q'>2q2q 

如果滿足上述條件，通過Wiener Attack可以在多項式時間中分解n。

rsa-wiener-attack的攻擊源碼開源在了github中，采取python編寫，可以很容易使用。

識別：

非常簡單，e看起來很大就行了。

例題：

直接github用工具就行。https://github.com/pablocelayes/rsa-wiener-attack

這里注意一個細節(jié)問題，如果在運行腳本的時候報錯，請在腳本前加上：

import sys  
sys.setrecursionlimit(10000000) 

0x05 共模攻擊

介紹：

如果在RSA的使用中使用了相同的模n對相同的明文m進行了加密，那么就可以在不分解n的情況下還原出明文m的值。

即：

c1≡me1'>c1≡me1c1≡me1 mod'>modmod n'>nn  
c2≡me2'>c2≡me2c2≡me2 mod'>modmod n'>nn 

此時不需要分解n，不需要求解私鑰，如果兩個加密指數(shù)互素，就可以通過共模攻擊在兩個密文和公鑰被嗅探到的情況下還原出明文m的值。

過程如下，首先兩個加密指數(shù)互質(zhì)，則：

(e1,e2)=1'>(e1,e2)=1(e1,e2)=1 

即存在s2'>s2s2，s2'>s2s2使得：

s1e1+s2e2=1'>s1e1+s2e2=1s1e1+s2e2=1 

又因為：

c1≡me1'>c1≡me1c1≡me1 mod'>modmod n'>nn  
c2≡me2'>c2≡me2c2≡me2 mod'>modmod n'>nn 

通過代入化簡可以得出：

c1s1c2s2≡m'>cs11cs22≡mc1s1c2s2≡m mod'>modmod n'>nn 

明文解出。

識別：

非常簡單，若干次加密，每次n都一樣，明文根據(jù)題意也一樣即可。

例題：

https://www.jarvisoj.com (very hard RSA)

如果已知：n1，n2，c1，c2，e1，e2，并且其中n1=n2的話：

s = egcd(e1, e2)  
s1 = s[1]  
s2 = s[2]  
print s  
n=n1  
if s1  
s1 = - s1  
c1 = modinv(c1, n)  
elif s2  
s2 = - s2  
c2 = modinv(c2, n)  
m=(pow(c1,s1,n)*pow(c2,s2,n)) % n