對大多數從事機器學習工作的人來說，設計一個神經網絡無異于制作一項藝術作品。神經網絡通常始于一個常見的架構，然后我們需要對參數不斷地進行調整和優化，直到找到一個好的組合層、激活函數、正則化器和優化參數。在一些知名的神經網絡架構，如VGG、Inception、ResNets、DenseNets等的指導下，我們需要對網絡的變量進行重復的操作，直到網絡達到我們期望的速度與準確度。隨著網絡處理能力的不斷提高，將網絡優化處理程序自動化變得越來越可行。

在像Random Forests和SVMs這樣的淺模型中，我們已經能夠使超參數優化的操作自動化進行了。一些常用的工具包，比如sk-learn，向我們提供了搜索超參數空間的方法。在其最簡單的、最基礎的格式中，“超參數”是我們在所有可能的參數中搜索得到的，或者是通過從參數分布中任意采樣得到的。（詳情請點擊此鏈接查看。）這兩種方法都面臨著兩個問題：***，在錯誤參數區域進行搜索時會造成資源浪費；第二，處理大量的動態特征參數集將導致效率過低。因此，改變處理器的架構變得相當困難。雖然現在有很多看似高效的方法，比如Bayesian優化方法。但Bayesian優化法雖然能夠解決了***個問題，卻對第二個問題無能為力；另外，在Bayesian優化設置中也很難進行探索模型。

自動識別***模型的想法就現在來說已經不算新鮮了，再加上最近大幅度提升的處理能力，實現這一想法比以往任何時候都要容易。

問題設定

考慮超參數優化的方式之一，就是將它看做一個“元學習問題”。

我們究竟能否打造出一個可以用于判斷網絡性能好壞的算法呢？

注意：接下來我將繼續使用“元學習”這個術語，即使將這個問題描述為“元學習”有點混淆視聽，但我們千萬不能把它與“學習”相關的一些方法弄混了。

 

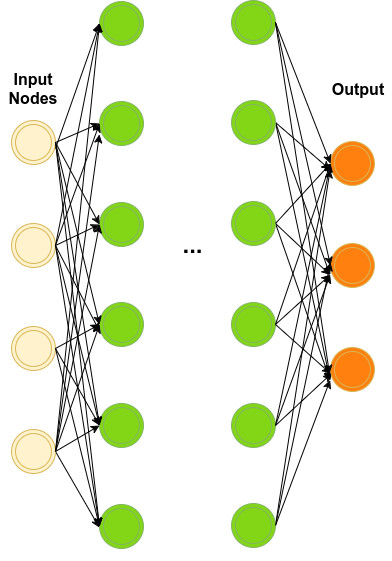
我們的目標是定義網絡隱含層（綠色）的數量以及每個隱含層的參數。

具體而言，就是探究模型架構和模型的參數空間，從而在給定的數據集上優化其性能。這個問題復雜難解，而回報稀薄。之所以說它回報稀薄，是因為我們需要對網絡進行足夠的訓練，還要對它進行評估；而在訓練、評估完成后，我們得到回報的僅僅是一些得分。這些得分反映了整個系統的性能表現，而這種類型的回報并不是可導函數！說到這，是不是讓你想起了什么呢？沒錯，這就是一個典型的“強化學習”情境！

維基百科對“強化學習”的定義：

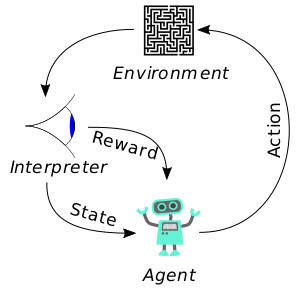
“強化學習”（RL）是一種重要的機器學習方法，它的靈感來自于心理學的行為主義理論。具體來說，“強化學習”是關于有機體（agent）如何在環境（environment）的刺激下，將累計獎勵***化的方法。

“強化學習”與標準的監督式學習之間的區別在于它不需要出現正確的輸入或輸出對，也不需要精準校正其次優化行為。另外，“在線性能”也是“強化學習”關注的焦點，即在未知領域的探索與現有知識的開發之間找到平衡。

 

上圖情境中的有機體（agent）是一個模型，環境（environment）就是我們用于訓練和評估的數據集。解釋器（interpreter）是對每一行為進行分析以及設置有機體狀態（在我們這個情境中，解釋器設置的是網絡參數）的過程。

通常情況下，“強化學習”問題都被定義為一個Markov決策過程。其目的就是優化有機體的總回報。每一步，你需要對優化模型輸出作出決策，或者是探索出一個新的行為。在環境的刺激下，有機體將根據得到的反饋，形成一個調整政策，不斷改進其行為。

注意：這個話題超出了本文討論的范圍，R.Sutton和A. Barto的《強化學習介紹》可能是關于這個主題的***入門指導書。

進化算法

解決“強化學習”問題的另一種方法是“進化算法”。在生物進化的啟發下，進化算法通過創建一個解決方案的集合，尋找解決方案的空間；然后，它會對每一解決方案進行評估，并根據評估得分不斷調整這個方案集合。生物進化論中所講的“進化”涉及到一個種群中***成員的選擇和變異。因此，我們的解決方案集合也會不斷進化發展，以提高其整體適應性，并為問題找到提供可行的解決方案。

 

上圖的左邊介紹了進化的過程，設計一個“進化算法”涉及到兩個部分——“選擇”，以及需要遵循的“跨界”或“變異”策略。

“選擇”：對于“選擇”，我們通常的做法是挑選***的個體和一些任意的個體，以達到多樣性。更先進的選擇方法是在種群下設立不同的“次群”，即“物種”；然后在物種中選擇***的個體，以保護其多樣性。另一種比較受歡迎的做法是“競賽選擇”，即任意選擇一些個體參與競賽，挑選出勝者（基因優勝的個體）。

“跨界”：“跨界”也稱“交叉跨界”，指的是兩組或兩組以上親本交叉混合，產生后代。“交叉跨界”高度依賴于問題結構的方式。常見的方法是用一個項目列表（一般是數值）對親本進行描述，然后從親本中挑選任意部分來生成新的基因組合。

“變異”：“變異”或“突變”指的是任意改變基因組的過程。這是主要的開發因素，有助于保持種群的多樣性。

實施啟用

“進化算法”的實施啟用使用了PyTorch來建立代理，這個代理將會探索用于完成簡單分類任務的DNNs。這個實驗使用的是MNIST，因為它小且快，即使在CPU上也能完成訓練。我們將建立一組DNN模型，并將其發展進化為N個步驟。

我們所講的“進化”主題實際上就是“物競天擇”的實施，完整的高水平“進化算法”如下所示：

new_population = [] 
  while size(new_population) < population_size: 
  choose k(tournament) individuals from the population at random 
  choose the best from pool/tournament with probability p1 
  choose the second best individual with probability p2 
  choose the third best individual with probability p3 
  mutate and append selected to the new_population 

附注：當涉及到架構合并時，跨界問題就變得相當復雜了。究竟該如何將兩個親本的架構合并呢？缺陷圖樣及環境整合訓練將對此產生什么影響呢？近期的一篇來自Miikkulainen等人的論文提出了一種被稱為CoDeepNEAT的解決方案。基于Evolino進化理論，一個架構由部分單元模塊組成，其中的每一單元模塊都是服從于進化理論的。這個架構是一個合并了所有組成成分的理想藍圖。在這樣的情境下，將親本的組成成分混合是十分合理的，因為其成分是一個完整的微型網絡。為了使文章更簡潔易懂，我在這個算法實施過程中避開了跨界交叉的問題，而是簡單介紹了類似NEAT（或CoDeepNEAT）這樣的解決方案。（我打算在下一篇文章中詳細介紹這些解決方案。）

基本的構件

我們需要定義的***件事情就是每一模型的解決方案空間，每一個個體都代表著一個架構。簡潔起見，我們堆疊了n層，每一層都包含三個參數：a)隱藏單元的數量；b)激活類型；c)丟失率。對于通用參數，我們在不同的優化器、學習率、權重衰減和層數量中進行選擇。

# definition of a space 
# lower bound - upper bound, type param, mutation rate 
LAYER_SPACE = dict() 
LAYER_SPACE['nb_units'] = (128, 1024, 'int', 0.15) 
LAYER_SPACE['dropout_rate'] = (0.0, 0.7, 'float', 0.2) 
LAYER_SPACE['activation'] =\ 
   (0,  ['linear', 'tanh', 'relu', 'sigmoid', 'elu'], 'list', 0.2) 
 
NET_SPACE = dict() 
NET_SPACE['nb_layers'] = (1, 3, 'int', 0.15) 
NET_SPACE['lr'] = (0.0001, 0.1, 'float', 0.15) 
NET_SPACE['weight_decay'] = (0.00001, 0.0004, 'float', 0.2) 
NET_SPACE['optimizer'] =\ 
   (0, ['sgd', 'adam', 'adadelta', 'rmsprop'], 'list', 0.2) 

完成以上操作以后，我們已經定義了模型的空間。接著我們還需要建立三個基本功能：

隨機選擇一個網絡

def random_value(space): 
   """Sample  random value from the given space.""" 
   val = None 
   if space[2] == 'int': 
       val = random.randint(space[0], space[1]) 
   if space[2] == 'list': 
       val = random.sample(space[1], 1)[0] 
   if space[2] == 'float': 
       val = ((space[1] - space[0]) * random.random()) + space[0] 
   return {'val': val, 'id': random.randint(0, 2**10)} 
 
 
def randomize_network(bounded=True): 
   """Create a random network.""" 
   global NET_SPACE, LAYER_SPACE 
   net = dict() 
   for k in NET_SPACE.keys(): 
       net[k] = random_value(NET_SPACE[k]) 
    
   if bounded:  
       net['nb_layers']['val'] = min(net['nb_layers']['val'], 1) 
    
   layers = [] 
   for i in range(net['nb_layers']['val']): 
       layer = dict() 
       for k in LAYER_SPACE.keys(): 
           layer[k] = random_value(LAYER_SPACE[k]) 
       layers.append(layer) 
   net['layers'] = layers 
   return net 

首先，我們任意地對層數量和每一層的參數進行采樣，樣本值會在預先定義好的范圍邊緣內出現下降。在初始化一個參數的同時，我們還會產生一個任意的參數id。現在它還不能使用，但我們可以追蹤所有的層。當一個新的模型發生突變時，舊的層會進行微調，同時僅對發生突變的層進行初始化。這樣的做法應該能夠顯著地加快速度，并穩定解決方案。

注意：根據問題性質的不同，我們可能需要不同的限制條件，比如參數的總量或層的總數量。

使網絡發生變異

def mutate_net(net): 
   """Mutate a network.""" 
   global NET_SPACE, LAYER_SPACE 
 
   # mutate optimizer 
   for k in ['lr', 'weight_decay', 'optimizer']: 
        
       if random.random() < NET_SPACE[k][-1]: 
           net[k] = random_value(NET_SPACE[k]) 
            
   # mutate layers 
   for layer in net['layers']: 
       for k in LAYER_SPACE.keys(): 
           if random.random() < LAYER_SPACE[k][-1]: 
               layer[k] = random_value(LAYER_SPACE[k]) 
   # mutate number of layers -- RANDOMLY ADD 
   if random.random() < NET_SPACE['nb_layers'][-1]: 
       if net['nb_layers']['val'] < NET_SPACE['nb_layers'][1]: 
           if random.random()< 0.5: 
               layer = dict() 
               for k in LAYER_SPACE.keys(): 
                   layer[k] = random_value(LAYER_SPACE[k]) 
               net['layers'].append(layer) 
               # value & id update 
               net['nb_layers']['val'] = len(net['layers']) 
               net['nb_layers']['id'] +=1 
           else: 
               if net['nb_layers']['val'] > 1: 
                   net['layers'].pop() 
                   net['nb_layers']['val'] = len(net['layers']) 
                   net['nb_layers']['id'] -=1 
   return net 

每一個網絡元素都存在變異的可能性，每一次變異都將重新采樣參數空間，進而使參數發生變化。

建立網絡

class CustomModel(): 
 
   def __init__(self, build_info, CUDA=True): 
 
       previous_units = 28 * 28 
       self.model = nn.Sequential() 
       self.model.add_module('flatten', Flatten()) 
       for i, layer_info in enumerate(build_info['layers']): 
           i = str(i) 
           self.model.add_module( 
               'fc_' + i, 
               nn.Linear(previous_units, layer_info['nb_units']['val']) 
               ) 
           self.model.add_module( 
               'dropout_' + i, 
               nn.Dropout(p=layer_info['dropout_rate']['val']) 
               ) 
           if layer_info['activation']['val'] == 'tanh': 
               self.model.add_module( 
                   'tanh_'+i, 
                   nn.Tanh() 
               ) 
           if layer_info['activation']['val'] == 'relu': 
               self.model.add_module( 
                   'relu_'+i, 
                   nn.ReLU() 
               ) 
           if layer_info['activation']['val'] == 'sigmoid': 
               self.model.add_module( 
                   'sigm_'+i, 
                   nn.Sigmoid() 
               ) 
           if layer_info['activation']['val'] == 'elu': 
               self.model.add_module( 
                   'elu_'+i, 
                   nn.ELU() 
               ) 
           previous_units = layer_info['nb_units']['val'] 
 
       self.model.add_module( 
           'classification_layer', 
           nn.Linear(previous_units, 10) 
           ) 
       self.model.add_module('sofmax', nn.LogSoftmax()) 
       self.model.cpu() 
        
       if build_info['optimizer']['val'] == 'adam': 
           optimizer = optim.Adam(self.model.parameters(), 
                               lr=build_info['weight_decay']['val'], 
                               weight_decay=build_info['weight_decay']['val']) 
 
       elif build_info['optimizer']['val'] == 'adadelta': 
           optimizer = optim.Adadelta(self.model.parameters(), 
                                   lr=build_info['weight_decay']['val'], 
                                   weight_decay=build_info['weight_decay']['val']) 
 
       elif build_info['optimizer']['val'] == 'rmsprop': 
           optimizer = optim.RMSprop(self.model.parameters(), 
                                   lr=build_info['weight_decay']['val'], 
                                   weight_decay=build_info['weight_decay']['val']) 
       else: 
           optimizer = optim.SGD(self.model.parameters(), 
                               lr=build_info['weight_decay']['val'], 
                               weight_decay=build_info['weight_decay']['val'], 
                               momentum=0.9) 
       self.optimizer = optimizer 
       self.cuda = False 
       if CUDA: 
           self.model.cuda() 
           self.cuda = True 

上面的類別將會實例化模型的“基因組”。

現在，我們已經具備了建立一個任意網絡、變更其架構并對其進行訓練的基本構件，那么接下來的步驟就是建立“遺傳算法”，“遺傳算法”將會對***個體進行選擇和變異。每個模型的訓練都是獨立進行的，不需要其他有機體的任何信息。這就使得優化過程可以隨著可用的處理節點進行線性擴展。

GP優化器的編碼

"""Genetic programming algorithms.""" 
from __future__ import absolute_import 
 
import random 
import numpy as np 
from operator import itemgetter 
import torch.multiprocessing as mp 
from net_builder import randomize_network 
import copy 
from worker import CustomWorker, Scheduler 
        
 
class TournamentOptimizer: 
   """Define a tournament play selection process.""" 
 
   def __init__(self, population_sz, init_fn, mutate_fn, nb_workers=2, use_cuda=True): 
       """ 
       Initialize optimizer. 
 
           params:: 
                
               init_fn: initialize a model 
               mutate_fn: mutate function - mutates a model 
               nb_workers: number of workers 
       """ 
        
       self.init_fn = init_fn 
       self.mutate_fn = mutate_fn 
       self.nb_workers = nb_workers 
       self.use_cuda = use_cuda 
        
       # population 
       self.population_sz = population_sz 
       self.population = [init_fn() for i in range(population_sz)]         
       self.evaluations = np.zeros(population_sz) 
        
       # book keeping 
       self.elite = [] 
       self.stats = [] 
       self.history = [] 
 
   def step(self): 
       """Tournament evolution step.""" 
       print('\nPopulation sample:') 
       for i in range(0,self.population_sz,2): 
           print(self.population[i]['nb_layers'], 
                 self.population[i]['layers'][0]['nb_units']) 
       self.evaluate() 
       children = [] 
       print('\nPopulation mean:{} max:{}'.format( 
           np.mean(self.evaluations), np.max(self.evaluations))) 
       n_elite = 2 
       sorted_pop = np.argsort(self.evaluations)[::-1] 
       elite = sorted_pop[:n_elite] 
        
       # print top@n_elite scores 
       # elites always included in the next population 
       self.elite = [] 
       print('\nTop performers:') 
       for i,e in enumerate(elite): 
           self.elite.append((self.evaluations[e], self.population[e]))     
           print("{}-score:{}".format( str(i), self.evaluations[e]))    
           children.append(self.population[e]) 
       # tournament probabilities: 
       # first p 
       # second p*(1-p) 
       # third p*((1-p)^2) 
       # etc... 
       p = 0.85 # winner probability  
       tournament_size = 3 
       probs = [p*((1-p)**i) for i in range(tournament_size-1)] 
       # a little trick to certify that probs is adding up to 1.0 
       probs.append(1-np.sum(probs)) 
        
       while len(children) < self.population_sz: 
           pop = range(len(self.population)) 
           sel_k = random.sample(pop, k=tournament_size) 
           fitness_k = list(np.array(self.evaluations)[sel_k]) 
           selected = zip(sel_k, fitness_k) 
           rank = sorted(selected, key=itemgetter(1), reverse=True) 
           pick = np.random.choice(tournament_size, size=1, p=probs)[0] 
           best = rank[pick][0] 
           model = self.mutate_fn(self.population[best]) 
           children.append(model) 
 
       self.population = children 
        
       # if we want to do a completely completely random search per epoch 
       # self.population = [randomize_network(bounded=False) for i in range(self.population_sz) ] 
 
   def evaluate(self): 
       """evaluate the models.""" 
        
       workerids = range(self.nb_workers) 
       workerpool = Scheduler(workerids, self.use_cuda ) 
       self.population, returns = workerpool.start(self.population) 
 
       self.evaluations = returns 
       self.stats.append(copy.deepcopy(returns)) 
       self.history.append(copy.deepcopy(self.population))  

“進化算法”看起來非常簡單，對嗎？沒錯！這個算法可以非常成功，尤其是當你為個體定義了好的變異或跨界功能時。

存儲庫中還包含了一些額外的使用類別，比如工作器類和調度器類，使GP優化器能夠獨立平行地完成模型訓練和評估。

運行代碼

按照上述步驟操作運行。

"""Tournament play experiment.""" 
from __future__ import absolute_import 
import net_builder 
import gp 
import cPickle 
# Use cuda ? 
CUDA_ = True 
 
if __name__=='__main__': 
   # setup a tournament! 
   nb_evolution_steps = 10 
   tournament = \ 
       gp.TournamentOptimizer( 
           population_sz=50, 
           init_fn=net_builder.randomize_network, 
           mutate_fn=net_builder.mutate_net, 
           nb_workers=3, 
           use_cuda=True) 
 
   for i in range(nb_evolution_steps): 
       print('\nEvolution step:{}'.format(i)) 
       print('================') 
       tournament.step() 
       # keep track of the experiment results & corresponding architectures 
       name = "tourney_{}".format(i) 
       cPickle.dump(tournament.stats, open(name + '.stats','wb')) 
       cPickle.dump(tournament.history, open(name +'.pop','wb')) 

接下來，讓我們一起來看看運行的結果！

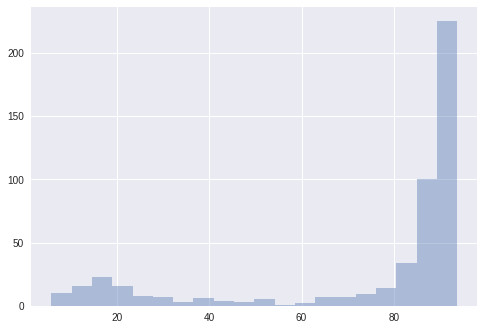
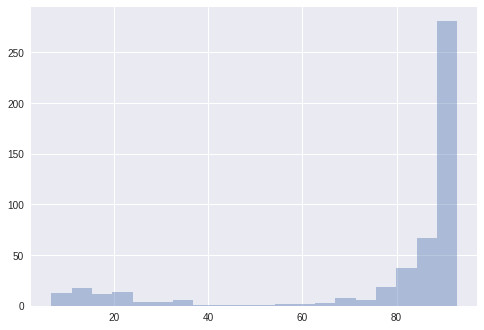
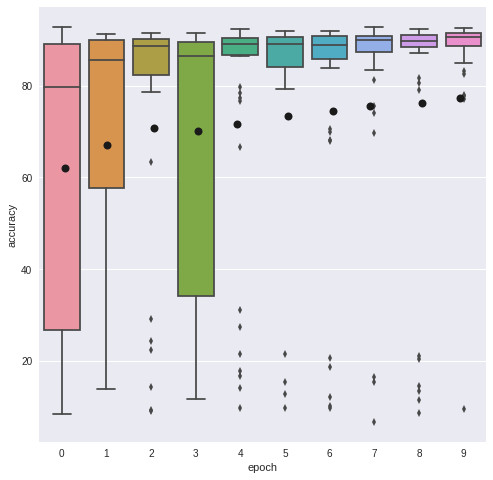
這是50個解決方案的得分結果，比賽規模為3。這些模型僅接受了10000個樣本的訓練，然后就被評估了。乍一看，進化算法似乎并沒有起到太大的作用，因為解決方案在***次進化中就已經接近***狀態了；而在第七階段，解決方案達到了它的***表現。在下圖中，我們用了一個盒式圖來依次描述這些解決方案的四分之一。我們發現，大多數方案都表現的很好，但在方案進化的同時，這個盒式圖也隨之緊縮了。

 

圖中的這個盒子展示了方案的四分之一，而其盒須則延伸展示了剩余四分之三的方案分布。其中的黑點代表著方案的平均值，從圖中我們會發現平均值的上升趨勢。

 

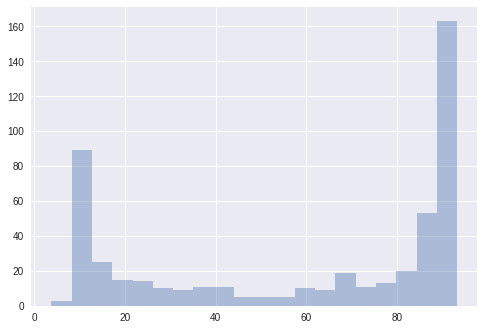
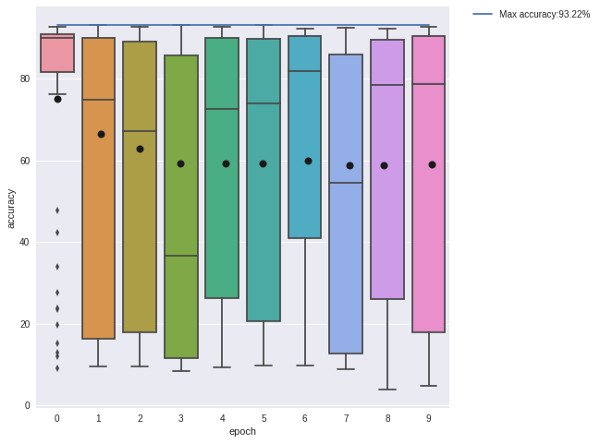
為了進一步理解這一方法的性能和表現，我們***將其與一個完全隨機的種群搜做相比較。每個階段之間都不需要進化，每個解決方案都要被重新設置為一個隨機的狀態。

在一個相對較小的（93.66% vs 93.22%）里進化算法的性能較好。而隨機種群搜索似乎生成了一些好的解決方案，但模型的方差卻大大增加了。這就意味著在搜索次優架構的時候出現了資源浪費。將這個與進化圖相比較，我們會發現進化確實生成了更多有用的解決方案，它成功地使那些結構進化了，進而使之達到了更好的性能表現。

• MNIST是一個相當簡單的數據集，即使是單層網絡也能達到很高的準確度。

• 像ADAM這樣的優化器對學習率的敏感度比較低，只有在它們的網絡具備足夠的參數時，它們才能找到比較好的解決方案。

• 在訓練過程中，模型只會查看10000個（訓練總數據的1/5）樣本示例。如果我們訓練得時間再長一些，好的架構可能會達到更高的準確度。

• 限制樣本數量對于我們學習的層的數量同樣非常重要，越深層的模型需要越多樣本。為了解決這個問題，我們還增加了一個移除突變層，使種群調節層的數量。

這個實驗的規模還不足以突出這種方法的優勢，這些文章中使用的實驗規模更大，數據集也更復雜。

我們剛剛完成了一個簡單的進化算法，這個算法很好地詮釋了“物競天擇”的主題。我們的算法只會選擇最終勝利的解決方案，然后將其變異來產生更多的后代。接下來，我們需要做的就是使用更先進的方法，生成和發展方案群。以下是一些改進的建議：

• 為通用層重新使用親本的權重

• 將來自兩個潛在親本的層合并

• 架構不一定要連續的，你可以探索層與層之間更多不一樣的聯系（分散或合并等）

• 在頂部增加額外的層，然后進行微調整。

以上內容都是人工智能研究領域的一個課題。其中一個比較受歡迎的方法就是NEAT及其擴展。EAT變量使用進化算法在開發網絡的同時，還對網絡的權重進行了設置。在一個典型的強化學習場景下，代理權重的進化是非常有可能實現的。但是，當(x,y)輸入對可用時，梯度下降的方法則表現得更好。

相關文章

Evolino: Hybrid Neuroevolution / Optimal Linear Search for Sequence Learning 

Evolving Deep Neural Networks — This is a very interesting approach of co-evolving whole networks and blocks within the network, it’s very similar to the Evolino method but for CNNs.

Large-Scale Evolution of Image Classifiers 

Convolution by Evolution

本文轉自雷鋒網，如需轉載請至雷鋒網官網申請授權。