神經網絡如何學習的?
像下山一樣,找到損失函數的最低點。
毫無疑問,神經網絡是目前使用的最流行的機器學習技術。所以我認為了解神經網絡如何學習是一件非常有意義的事。
為了能夠理解神經網絡是如何進行學習的,讓我們先看看下面的圖片:
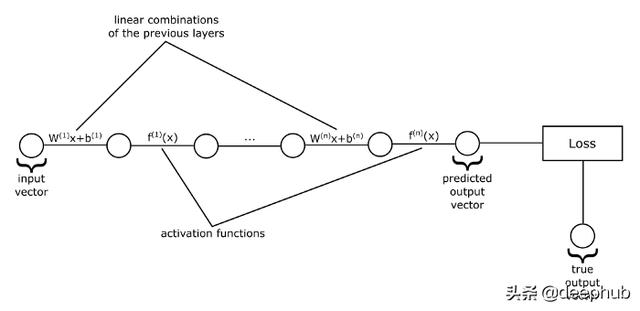
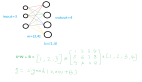
如果我們把每一層的輸入和輸出值表示為向量,把權重表示為矩陣,把誤差表示為向量,那么我們就得到了上述的一個神經網絡的視圖,它只是一系列向量函數的應用。也就是說,函數將向量作為輸入,對它們進行一些轉換,然后把變換后的向量輸出。在上圖中,每條線代表一個函數,它可以是一個矩陣乘法加上一個誤差向量,也可以是一個激活函數。這些圓表示這些函數作用的向量。
例如,我們從輸入向量開始,然后將其輸入到第一個函數中,該函數用來計算其各分量的線性組合,然后我們將獲得的向量作為輸出。然后把這個向量作為激活函數的輸入,如此類推,直到我們到達序列中的最后一個函數。最后一個函數的輸出就是神經網絡的預測值。
到目前為止,我們已經討論過神經網絡是如何得到輸出的,這正是我們感興趣的內容。我們知道神經網絡只是將它的輸入向量傳遞給一系列函數。但是這些函數要依賴于一些參數:權重和誤差。
神經網絡如何通過學習得到這些參數來獲得好的預測呢?
讓我們回想一下神經網絡實際上是什么:實際上它只是一個函數,是由一個個小函數按順序排列組成的大函數。這個函數有一組參數,在一開始,我們并不知道這些參數應該是什么,我們僅僅是隨機初始化它們。因此在一開始神經網絡會給我們一些隨機的值。那么我們如何改進他們呢?在嘗試改進它們之前,我們首先需要一種評估神經網絡性能的方法。如果我們沒有辦法衡量模型的好壞,那么我們應該如何改進模型的性能?
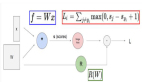
為此,我們需要設計一個函數,這個函數將神經網絡的預測值和數據集中的真實標簽作為輸入,將一個代表神經網絡性能的數字作為輸出。然后我們就可以將學習問題轉化為求函數的最小值或最大值的優化問題。在機器學習領域,這個函數通常是用來衡量我們的預測有多糟糕,因此被稱為損失函數。我們的問題就變成了找到使這個損失函數最小化的神經網絡參數。
隨機梯度下降算法
你可能很擅長從微積分中求函數的最小值。對于這種問題,通常取函數的梯度,令其等于0,求出所有的解(也稱為臨界點),然后從中選擇使函數值最小的那一個。這就是全局最小值。我們能做同樣的事情來最小化我們的損失函數嗎?事實上是行不通的,主要的問題是神經網絡的損失函數并不像微積分課本中常見的那樣簡潔明了。它是一個極其復雜的函數,有數千個、幾十萬個甚至數百萬個參數。有時甚至不可能找到一個解決問題的收斂解。這個問題通常是通過迭代的方法來解決的,這些方法并不試圖找到一個直接的解,而是從一個隨機的解開始,并在每次迭代中嘗試改進一點。最終,經過大量的迭代,我們將得到一個相當好的解決方案。
其中一種迭代方法是梯度下降法。你可能知道,一個函數的梯度給出了最陡的上升方向,如果我們取梯度的負值,它會給我們最陡下降的方向,也就是我們可以在這個方向上最快地達到最小值。因此,在每一次迭代(也可以將其稱作一次訓練輪次)時,我們計算損失函數的梯度,并從舊參數中減去它(乘以一個稱為學習率的因子)以得到神經網絡的新參數。
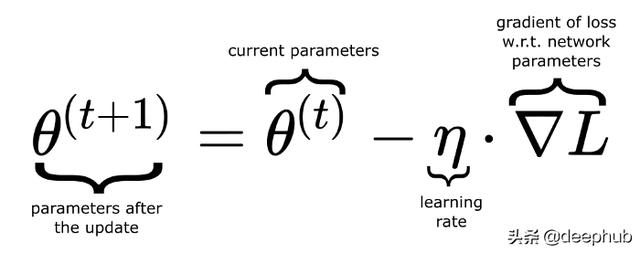
其中θ(theta)表示包含神經網絡所有參數的向量。
在標準梯度下降法中,梯度是將整個數據集考慮進來并進行計算的。通常這是不可取的,因為該計算可能是昂貴的。在實踐中,數據集被隨機分成多個塊,這些塊被稱為批。對每個批進行更新。這種方法就叫做隨機梯度下降。
上面的更新規則在每一步只考慮在當前位置計算的梯度。這樣,在損失函數曲面上運動的點的軌跡對任何變動都很敏感。有時我們可能想讓這條軌跡更穩健。為此,我們使用了一個受物理學啟發的概念:動量。我們的想法是,當我們進行更新時,也考慮到以前的更新,這會累積成一個變量Δθ。如果在同一個方向上進行更多的更新,那么我們將"更快"地朝這個方向前進,并且不會因為任何小的擾動而改變我們的軌跡。把它想象成速度。
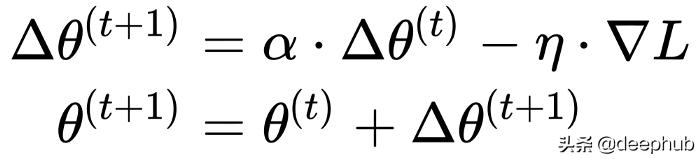
其中α是非負因子,它可以決定舊梯度到底可以貢獻多少值。當它為0時,我們不使用動量。
反向傳播算法
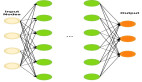
我們如何計算梯度呢?回想一下神經網絡和損失函數,它們只是一個函數的組合。那么如何計算復合函數的偏導數呢?我們可以使用鏈式法則。讓我們看看下面的圖片:
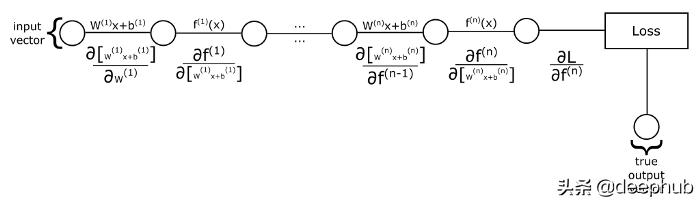
如果我們要計算損失函數對第一層權重參數的偏導數:我們首先讓第一個線性表達式對權重參數求偏導,然后用這個結果乘上下一個函數(也就是激活函數)關于它前面函數輸出內容的偏導數,一直執行這個操作,直到我們乘上損失函數關于最后一個激活函數的偏導數。那如果我們想要計算對第二層的權重參數求的導數呢?我們必須做同樣的過程,但是這次我們從第二個線性組合函數對權重參數求導數開始,然后,我們要乘的其他項在計算第一層權重的導數時也出現了。所以,與其一遍又一遍地計算這些術語,我們將從后向前計算,因此得名為反向傳播算法。
我們將首先計算出損失函數關于神經網絡輸出層的偏導數,然后通過保持導數的運行乘積將這些導數反向傳播到第一層。需要注意的是,我們有兩種導數:一種是函數關于它輸入內容的導數。我們把它們乘以導數的乘積,目的是跟蹤神經網絡從輸出層到當前層神經元節點的誤差。第二類導數是關于參數的,這類導數是我們用來優化參數的。我們不把它與其它導數的乘積相乘,相反,我們將它們存儲為梯度的一部分,稍后我們將使用它來更新參數。
所以,在反向傳播時,當我們遇到沒有可學習參數的函數時(比如激活函數),我們只取第一種的導數,只是為了反向傳播誤差。但是,當我們遇到的函數有可學的參數(如線性組合,有權重和偏差),那么我們取這兩種導數:第一種是用誤差傳播的輸入,第二種是加權和偏差,并將它們作為梯度的一部分來存儲。整個過程,我們從損失函數開始,直到我們到達第一層,在這一層我們沒有任何想要添加到梯度中的可學習參數。這就是反向傳播算法。
Softmax激活和交叉熵損失函數
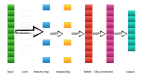
分類任務中,最后一層常用的激活函數是softmax函數。
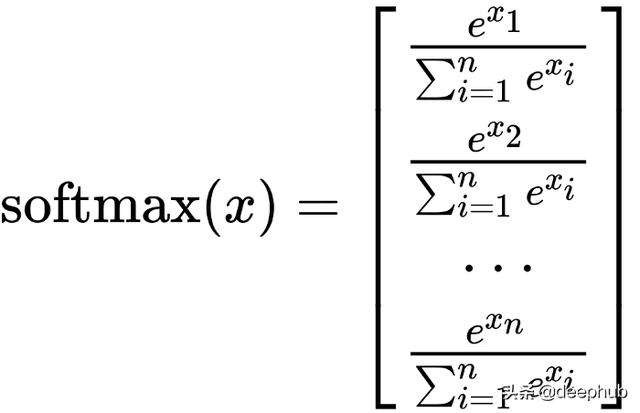
softmax函數將其輸入向量轉換為概率分布。從上圖中可以看到softmax的輸出的向量元素都是正的,它們的和是1。當我們使用softmax激活時,我們在神經網絡最后一層創建與數據集中類數量相等的節點,并且softmax激活函數將給出在可能的類上的概率分布。因此,神經網絡的輸出將會把輸入向量屬于每一個可能類的概率輸出給我們,我們選擇概率最高的類作為神經網絡的預測。
當把softmax函數作為輸出層的激活函數時,通常使用交叉熵損失作為損失函數。交叉熵損失衡量兩個概率分布的相似程度。我們可以將輸入值x的真實標簽表示為一個概率分布:其中真實類標簽的概率為1,其他類標簽的概率為0。標簽的這種表示也被稱為一個熱編碼。然后我們用交叉熵來衡量網絡的預測概率分布與真實概率分布的接近程度。
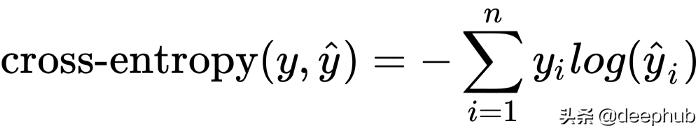
其中y是真標簽的一個熱編碼,y hat是預測的概率分布,yi,yi hat是這些向量的元素。
如果預測的概率分布接近真實標簽的一個熱編碼,那么損失函數的值將接近于0。否則如果它們相差很大,損失函數的值可能會無限大。
均方誤差損失函數
softmax激活和交叉熵損失主要用于分類任務,而神經網絡只需在最后一層使用適當的損失函數和激活函數就可以很容易地適應回歸任務。例如,如果我們沒有類標簽作為依據,我們有一個我們想要近似的數字列表,我們可以使用均方誤差(簡稱MSE)損失函數。通常,當我們使用MSE損失函數時,我們在最后一層使用身份激活(即f(x)=x)。
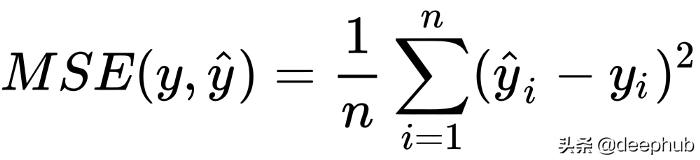
綜上所述,神經網絡的學習過程只不過是一個優化問題:我們要找到使損失函數最小化的參數。但這不是一件容易的事,有很多關于優化技術的書。而且,除了優化之外,對于給定的任務選擇哪種神經網絡結構也會出現問題。
我希望這篇文章對你有幫助,并十分感謝你的閱讀。