[[201540]]

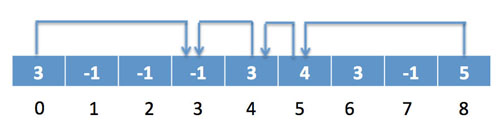
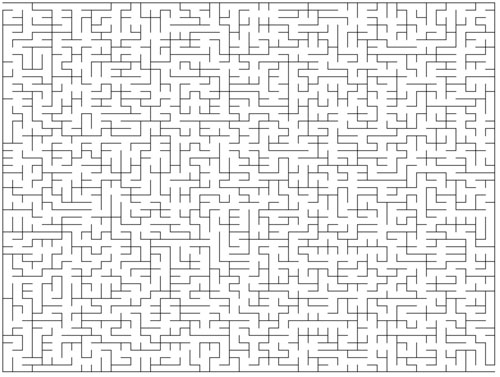
本篇將嘗使用canvas + wasm畫一個迷宮，生成算法主要用到連通集算法，使用wasm主要是為了提升運行效率。然后再用一個最短路徑算法找到迷宮的出路，***的效果如下：

1. 用連通集算法生成迷宮

生成迷宮的算法其實很簡單，假設迷宮的大小是10 * 10，即這個迷宮有100個格子，通過不斷地隨機拆掉這100個格子中間的墻，直到可以從***個格子走到***一個格子，也就是說***個格子和***一個格子處于同一個連通集。具體如下操作：

(1)生成100個格子，每個格子都不相通

(2)隨機選取相鄰的兩個格子，可以是左右相鄰或者是上下相鄰，判斷這兩個格子是不是處于同一個連通集，即能否從其中一個格子走到另外一個格子，如果不能，就拆掉它們中間的墻，讓它們相連，處于同一個連通集。

(3)重復第二步，直到***個格子和***一個格子相連。

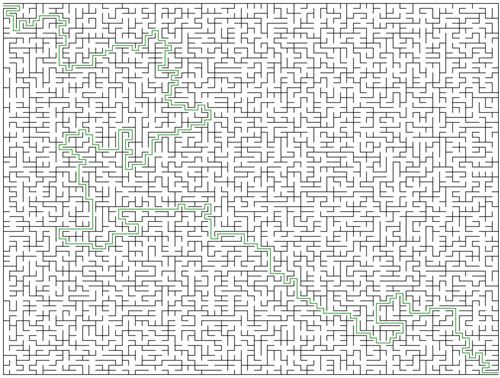
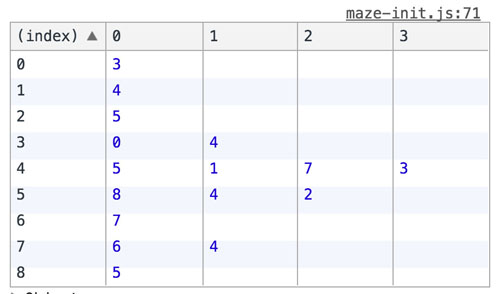
那這個連通集應該怎么表示呢?我們用一個一維數組來表示不同的已連通的集合，初始化的時候每個格子的值都為-1，如下圖所示，假設迷宮為3 * 3，即有9個格子：

每個索引在迷宮的位置：

負數表示它們是不同的連通集，因為我們還沒開始拆墻，所以一開始它們都是獨立的。

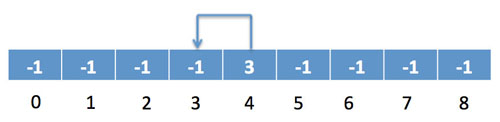
現在把3、4中間的墻拆掉，也就是說讓3和4連通，把4的值置成3，表示4在3這個連通集，3是它們的根，如下圖所示：

再把5、8給拆了：

再把4、5給拆了：

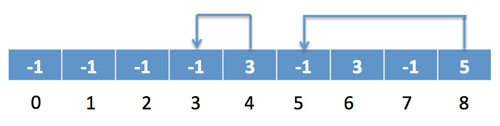
這個時候3、4、5、8就處于同一個連通集了，但是0和8依舊是兩個不同的連通集，這個時候再把3和0中間的墻給拆了：

由于0的連通集是3，而8的連通集也是3，即它們處于同一個連通集，因此這個時候從***個格子到***一個格子的路是相通的，就生成了一個迷宮。

我們用UnionSet的類表示連通集，如下代碼所示：

class UnionSet{ 
    constructor(size){ 
        this.set = new Array(size); 
        for(var i = this.set.length - 1; i >= 0; i--){ 
            this.set[i] = -1; 
        } 
    } 
    union(root1, root2){ 
        this.set[root1] = root2; 
    } 
    findSet(x){ 
        while(this.set[x] >= 0){ 
            x = this.set[x]; 
        } 
        return x; 
    } 
    sameSet(x, y){ 
        return this.findSet(x) === this.findSet(y); 
    } 
    unionElement(x, y){ 
        this.union(this.findSet(x), this.findSet(y)); 
    } 
} 

我們總共用了22行代碼就實現了一個連通集。上面的代碼應該比較好理解，對照上面的示意圖。如findSet函數得到某個元素所在的set的根元素，而根元素存放的是負數，只要存放的值是正數那么它就是指向另一個結點，通過while循環一層層的往上找直到負數。unionElement可以連通兩個元素，先找到它們所在的set，然后把它們的set union一下變成同一個連通集。

現在寫一個Maze，用來控制畫迷宮的操作，它組合一個UnionSet的實例，如下代碼所示：

class Maze{ 
    constructor(columns, rows, cavans){ 
        this.columns = columns; 
        this.rows = rows; 
        this.cells = columns * rows; 
        //存放是連通的格子，{1: [2, 11]}表示第1個格子和第2、11個格子是相通的 
        this.linkedMap = {}; 
        this.unionSets = new UnionSet(this.cells); 
        this.canvas = canvas; 
    } 
} 

Maze構造函數傳三個參數，前兩個是迷宮的列數和行數，***一個是canvas元素。在構造函數里面初始化一個連通集，作為這個Maze的核心模型，還初始化了一個linkedMap，用來存放拆掉的墻，進而提供給canvas繪圖。

Maze類再添加一個生成迷宮的函數，如下代碼所示：

//生成迷宮 
generate(){ 
    //每次任意取兩個相鄰的格子，如果它們不在同一個連通集， 
    //則拆掉中間的墻，讓它們連在一起成為一個連通集 
    while(!this.firstLastLinked()){ 
        var cellPairs = this.pickRandomCellPairs(); 
        if(!this.unionSets.sameSet(cellPairs[0], cellPairs[1])){ 
            this.unionSets.unionElement(cellPairs[0], cellPairs[1]); 
            this.addLinkedMap(cellPairs[0], cellPairs[1]); 
        }    
    }    
} 

生成迷宮的核心邏輯很簡單，在while循環里面判斷***個是否與***一個格子連通，如果不是的話，則每次隨機選取兩個相鄰的格子，如果它們不在同一個連通集，則把它們連通一下，同時記錄一下拆掉的墻到linkedMap里面。

怎么隨機選取兩個相鄰的格子呢?這個雖然沒什么技術難點，但是實現起來需要動一番腦筋，因為在邊上的格子沒有完整的上下左右四個相鄰格子，有些只有兩個，有些有三個。筆者是這么實現的，相對來說比較簡單：

//取出隨機的兩個挨著的格子 
pickRandomCellPairs(){ 
    var cell = (Math.random() * this.cells) >> 0; 
    //再取一個相鄰格子，0 = 上，1 = 右，2 = 下，3 = 左 
    var neiborCells = [];  
    var row = (cell / this.columns) >> 0, 
        column = cell % this.rows; 
    //不是***排的有上方的相鄰元素 
    if(row !== 0){  
        neiborCells.push(cell - this.columns); 
    }    
    //不是***一排的有下面的相鄰元素 
    if(row !== this.rows - 1){  
        neiborCells.push(cell + this.columns); 
    }    
    if(column !== 0){  
        neiborCells.push(cell - 1);  
    }    
    if(column !== this.columns - 1){  
        neiborCells.push(cell + 1);  
    }    
    var index = (Math.random() * neiborCells.length) >> 0; 
    return [cell, neiborCells[index]]; 
} 

首先隨機選一個格子，然后得到它的行數和列數，接著依次判斷它的邊界情況。如果它不是處于***排，那么它就有上面一排的相鄰格子，如果不是***一排則有下面一排的相鄰格子，同理，如果不是在***列則有左邊的，不是***一列則有右邊的。把符合條件的格子放到一個數組里面，然后再隨機取這個數組里的一個元素。這樣就得到了兩個隨機的相鄰元素。

另一個addLinkedMap函數的實現較為簡單，如下代碼所示：

addLinkedMap(x, y){ 
    if(!this.linkedMap[x]) this.linkedMap[x] = []; 
    if(!this.linkedMap[y]) this.linkedMap[y] = []; 
    if(this.linkedMap[x].indexOf(y) < 0){ 
        this.linkedMap[x].push(y); 
    } 
    if(this.linkedMap[y].indexOf(x) < 0){ 
        this.linkedMap[y].push(x); 
    } 
} 

這樣生成迷宮的核心邏輯基本完成，但是上面連通集的代碼可以優化， 一個是findSet函數，可以在findSet的時候把當前連通集里的元素的存放值直接改成根元素，這樣就不用形成一條很長的查找鏈，或者說形成一棵很高的樹，可直接一步到位，如下代碼所示：

findSet(x){ 
    if(this.set[x] < 0) return x; 
    return this.set[x] = this.findSet(this.set[x]); 
} 

這段代碼使用了一個遞歸，在查找的同時改變值。

union函數也可以做一個優化，findSet可以把樹的高度改小，但是在沒有改小前的union操作也可以做優化，如下代碼所示：

union(root1, root2){ 
    if(this.set[root1] < this.set[root2]){ 
        this.set[root2] = root1; 
    } else { 
        if(this.set[root1] === this.set[root2]){ 
            this.set[root2]--; 
        }    
        this.set[root1] = root2; 
    }    
} 

這段代碼的目的也是為了減少查找鏈的長度或者說減少樹的高度，方法是把一棵比較矮的連通集成為另外一棵比較高的連通集的子樹，這樣兩個連通集，合并起來的高度還是那棵高的。如果兩個連通集的高度一樣，則選取其中一個作為根，另外一棵樹的結點在查找的時候無疑這些結點的查找長度要加上1 ，因為多了一個新的root，也就是說樹的高度要加1，由于存放的是負數，所以進行減減操作。在判斷樹高度的時候也是一樣的，越小就說明越高。

經驗證，這樣改過之后，代碼執行效率快了一半以上。

迷宮生成好之后，現在開始來畫。

2. 用Canvas畫迷宮

先寫一個canvas的html元素，如下代碼所示：

<canvas id="maze" width="800" height="600"></canvas> 

注意canvas的寬高要用width和height的屬性寫，如果用style的話就是拉伸了，會出現模糊的情況。

怎么用canvas畫線呢?如下代碼所示：

var canvas = document.getElementById("maze"); 
var ctx = canvas.getContext("2d"); 
ctx.moveTo(0, 0); 
ctx.lineTo(100, 100); 
ctx.stroke(); 

這段代碼畫了一條線，從(0, 0)到(100, 100)，這也是本篇將用到的canvas的3個基礎的api。

上面已經得到了一個linkedMap，對于一個3 * 3的表格，把linkedMap打印一下，可得到以下表格。

通過上面的表格可知道，0和3中間是沒有墻，所以在畫的時候0和3中間就不要畫橫線了，3和4也是相連的，它們中間就不要畫豎線了。對每個普通的格子都畫它右邊的豎線和下面的橫線，而對于被拆掉的就不要畫，所以得到以下代碼：

draw(){  
    var linkedMap = this.linkedMap; 
    var cellWidth = this.canvas.width / this.columns, 
        cellHeight = this.canvas.height / this.rows; 
    var ctx = this.canvas.getContext("2d"); 
    //translate 0.5個像素，避免模糊 
    ctx.translate(0.5, 0.5); 
    for(var i = 0; i < this.cells; i++){ 
        var row = i / this.columns >> 0, 
            column = i % this.columns; 
        //畫右邊的豎線 
        if(column !== this.columns - 1 && (!linkedMap[i] || linkedMap[i].indexOf(i + 1) < 0)){ 
            ctx.moveTo((column + 1) * cellWidth >> 0, row * cellHeight >> 0); 
            ctx.lineTo((column + 1) * cellWidth >> 0, (row + 1) * cellHeight >> 0); 
        } 
        //畫下面的橫線 
        if(row !== this.rows - 1 && (!linkedMap[i] || linkedMap[i].indexOf(i + this.columns) < 0)){ 
            ctx.moveTo(column * cellWidth >> 0, (row + 1) * cellHeight >> 0); 
            ctx.lineTo((column + 1) * cellWidth >> 0, (row + 1) * cellHeight >> 0); 
        } 
    } 
    //***再一次性stroke，提高性能 
    ctx.stroke(); 
    //畫迷宮的四條邊框 
    this.drawBorder(ctx, cellWidth, cellHeight); 
} 

上面的代碼也比較好理解，在畫右邊的豎線的時候，先判斷它和右邊的格子是否相通，即linkMap[i]里面有沒有i + 1元素，如果沒有，并且它不是***一列，就畫右邊的豎線。因為迷宮的邊框放到后面再畫，它比較特殊，***一個格子的豎線是不要畫的，因為它是迷宮的出口。每次moveTo和lineTo的位置需要計算一下。

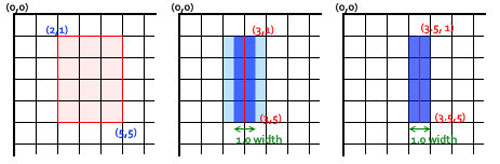
注意上面的代碼做了兩個優化，一個是先translate 0.5個像素，為了讓canvas畫線的位置剛好在像素上面，因為我們的lineWidth是1，如果不translate，那么它畫的位置如下圖中間所示，相鄰兩個像素占了半個像素，顯示器顯示的時候變會變虛，而translate 0.5個像素之后，它就會剛好畫在像在像素點上。詳見：HTML5 Canvas – Crisp lines every time。

第二個優化是所有的moveTo和lineTo都完成之后再stroke，這樣它就是一條線，可以極大地提高畫圖的效率。這個很重要，剛開始的時候沒這么做，導致格子數稍多的時候就畫不了了，改成這樣之后，繪制的效率提升很多。

我們還可以再做一個優化，就是使用雙緩存技術，在畫的時候別直接畫到屏幕上，而是先在內存的畫布里面完成繪制，***再一次性地Paint繪制到屏幕上，這樣也可以提高性能。如下代碼所示：

draw(){ 
    var canvasBuffer = document.createElement("canvas"); 
    canvasBuffer.width = this.canvas.width; 
    canvasBuffer.height = this.canvas.height; 
    var ctx = canvasBuffer.getContext("2d"); 
    ctx.translate(0.5, 0.5); 
    for(var i = 0; i < this.cells; i++){ 
  
    }    
    ctx.stroke(); 
    this.drawBorder(ctx, cellWidth, cellHeight); 
    console.log("draw"); 
    this.canvas.getContext("2d").drawImage(canvasBuffer, 0, 0);  
} 

先動態創建一個canvas節點，獲取它的context，在上面畫圖，畫好之后再用原先的canvas的context的drawImage把它畫到屏幕上去。

然后就可以寫驅動代碼了，如下畫一個50 * 50的迷宮，并統計一下時間：

const column = 50, 
      row = 50; 
var canvas = document.getElementById("maze"); 
var maze = new Maze(column, row, canvas); 
  
console.time("generate maze"); 
maze.generate(); 
console.timeEnd("generate maze"); 
console.time("draw maze"); 
maze.draw(); 
console.timeEnd("draw maze"); 

畫出的迷宮：

運行時間：

可以看到畫一個2500規模的迷宮，draw的時間還是很少的，而生成的時間也不長，但是我們發現一個問題，就是迷宮的有些格子是封閉的：

這些不能夠進去的格子就沒用了，這不太符合迷宮的特點。所以不能存在自我封閉的格子，由于生成的時候是判斷***個格子有沒有和***一個連通，現在改成***個格子和所有的格子都是連通的，也就是說可以從***個格子到達任意一個格子，這樣迷宮的誤導性才比較強，如下代碼所示：

linkedToFirstCell(){ 
    for(var i = 1; i < this.cells; i++){ 
        if(!this.unionSets.sameSet(0, i))  
            return false; 
    }    
    return true; 
} 

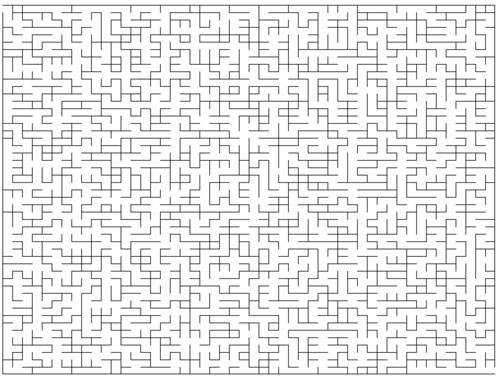
把while的判斷也改一下，這樣改完之后，生成的迷宮變成了這樣：

這樣生成的迷宮看起來就正常多了，生成迷宮的時間也相應地變長：

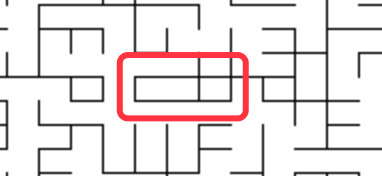
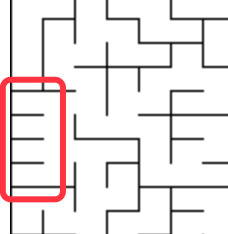
但是我們發現還是有一些比較奇怪的格子布局，如下圖所示：

因為這樣布局的其實沒太大的意義，如果讓你手動設計一個迷宮，你肯定也不會設計這樣的布局。所以我們的算法還可以再改進，由于上面是隨機選取兩個相鄰格子，可以把它改成隨機選取4個相鄰的格子，這樣生成的迷宮通道就會比較長，像上圖這種比較奇芭的情況就會比較少。讀者可以親自動手試驗一下。

3. 用最短路徑算法找到迷宮的出路

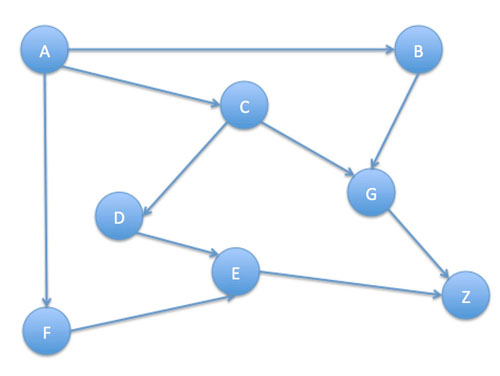
這個模型更為常見的場景是，現在我在A城鎮，準備去Z城鎮，中間要繞道B、C、D等城鎮，并且有多條路線可選，并且知道每個城鎮和它連通的城鎮以及兩兩之間距離，現在要求解一條A到Z的最短的路，如下圖所示：

在迷宮的模型里面也是類似的，要求解從***個格子到***一個格子的最短路徑，并且已經知道格子之間的連通情況。不一樣的是相鄰格子之間的距離是無權的，都為1，所以這個處理起來會更加簡單。

用一個貪婪算法可以解決這個問題，假設從A到Z的最短路徑為A->C->G->Z，那么這條路徑也是A到G、A到C的最短路徑，因為如果A到G還有更短的路徑，那么A到Z的距離就還可以更短了，即這條路徑不是最短的。因此我們從A開始延伸，一步步地確定A到其它地點的最短路徑，直到擴散到Z。

在無權的情況下，如上面任意相鄰城鎮的距離相等，和A直接相連的節點必定是A到這個節點的最短路徑，如上圖A到B、C、F的最短路徑為A->B、A->C、A->F，這三個點的最短路徑可標記為已知。和C直接相鄰的是G和D，C是最短的，所以A->C-G和A->C->D也是最短的，再往下一層，和G、D直接相連的分別是E和Z，所以A->C->G->Z和A->C->D->E是到Z和E的一條最短路徑，到此就找到了A->Z的最短路線。E也可以到Z，但是由于Z已經被標為已知最短了，所以通過E的這條路徑就被放棄了。

和A直接相連的做為***層，而和***層直接相連的做為第二層，由***層到第二層一直延伸目標結點，先被找到的節點就會被標記為已知。這是一個廣度優先搜索。

而在有權的情況下，剛開始的時候A被標記為已知，由于A和C是最短的，所以C也被標記為已知，B和F不會標記，但是它們和A的距離會受到更新，由初始化的無窮大更新為A->B和A->F的距離。在已查找到但未標記的兩個點里面，A->F的距離是最短的，所以F被標記為已知，這是因為如果存在另外一條更短的未知的路到F，它必定得先經過已經查找到的點(因為已經查找過的點是A的必經之路)，這里面已經是最短的了，所以不可能還有更短的了。F被標記為已知之后和F直接相連的E的距離得到更新，同樣地，在已查找到但未標記的點里面B的距離最短，所以B被標記為已知，然后再更新和B相連的點的距離。重復這個過程，直到Z被標記為已知。

標記起始點為已知，更新表的距離，再標記表里最短的距離為已知，再更新表的距離，重復直到目的點被標記，這個算法也叫Dijkstra算法。

現在來實現一個無權的最短路徑，如下代碼所示：

calPath(){ 
    var pathTable = new Array(this.cells); 
    for(var i = 0; i < pathTable.length; i++){ 
        pathTable[i] = {known: false, prevCell: -1}; 
    }    
    pathTable[0].known = true; 
    var map = this.linkedMap; 
    //用一個隊列存儲當前層的節點，先進隊列的結點優先處理 
    var unSearchCells = [0]; 
    var j = 0; 
    while(!pathTable[pathTable.length - 1].known){ 
        while(unSearchCells.length){ 
            var cell = unSearchCells.pop(); 
            for(var i = 0; i < map[cell].length; i++){ 
                if(pathTable[map[cell][i]].known) continue; 
                pathTable[map[cell][i]].known = true; 
                pathTable[map[cell][i]].prevCell = cell;  
                unSearchCells.unshift(map[cell][i]); 
                if(pathTable[pathTable.length - 1].known) break; 
            }    
        }    
    }    
    var cell = this.cells - 1; 
    var path = [cell]; 
    while(cell !== 0){  
        var cell = pathTable[cell].prevCell; 
        path.push(cell); 
    }    
    return path; 
} 

這個算法實現的關鍵在于用一個隊列存儲未處理的結點，每處理一個結點時，就把和這個結點相連的點入隊，這樣新入隊的結點就會排到當前層的結點的后面，當把***層的結點處理完了，就會把第二層的結點都push到隊尾，同理當把第二層的結點都出隊了，就會把第三層的結點推到隊尾。這樣就實現了一個廣度優先搜索。

在處理每個結點需要需要先判斷一下當前結點是否已被標記為known，如果是的話就不用處理了。

在pathTable表格里面用一個prevCell記錄到這個結點的上一個結點是哪個，為了能夠從目的結點一直往前找到到達***個結點的路徑。***找到這個path返回。

只要有這個path，就能夠計算位置畫出路徑的圖，如下圖所示：

這個算法的速度還是很快的，如下圖所示：

當把迷宮的規模提高到200 * 200時：

生成迷宮的時間就很耗時了，花費了10秒：

于是想著用WASM提高生成迷宮的效率，看看能提升多少。我在《WebAssembly與程序編譯》這篇里已經介紹了WASM的一些基礎知識，本篇我將用它來生成迷宮。

4. 用WASM生成迷宮

我在《WebAssembly與程序編譯》提過用JS寫很難編譯，所以本篇也直接用C來寫。上面是用的class，但是WASM用C寫沒有class的類型，只支持基本的操作。但是可以用一個struct存放數據，函數名也相應地做修改，如下代碼所示：

struct Data{ 
    int *set; 
    int columns; 
    int rows; 
    int cells; 
    int **linkedMap; 
} data; 
  
void Set_union(int root1, int root2){ 
    int *set = data.set; 
    if(set[root1] < set[root2]){ 
        set[root2] = root1; 
    } else { 
        if(set[root1] == set[root2]){ 
            set[root2]--; 
        } 
        set[root1] = root2; 
    } 
} 
  
int Set_findSet(int x){ 
    if(data.set[x] < 0) return x; 
    else return data.set[x] = Set_findSet(data.set[x]); 
} 

數據類型都是強類型的，函數名以類名Set_開頭，類的數據放在一個struct結構里面。主要導出函數為：

#include <emscripten.h> 
  
EMSCRIPTEN_KEEPALIVE //這個宏表示這個函數要作為導出的函數 
int **Maze_generate(int columns, int rows){ 
    Maze_init(columns, rows); 
    Maze_doGenerate(); 
    return data.linkedMap; 
    //return Maze_getJSONStr();  
} 

傳進來列數和行數，返回一個二維數組。其它代碼相應地改成C代碼，這里不再放出來。需要注意的是，由于這里用到了一些C內置的庫，如使用隨機數函數rand()，所以不能用上文提到的生成wasm的方法，不然會報rand等庫函數沒有定義。

把生成wasm的命令改成：

emcc maze.c -Os -s WASM=1 -o maze-wasm.html

這樣它會生成一個maze-wasm.js和maze-wasm.wasm(生成的html文件不需要用到)，生成的JS文件是用來自動加載和導入wasm文件的，在html里面引入這個JS：

<script src="maze-wasm.js"></script> 
<script src="maze.js"></script> 

它就會自動去加載maze-wasm.wasm文件，同時會定義一個全局的Module對象，在wasm文件加載好之后會觸發onInit，所以調它的api添加一個監聽函數，如下代碼所示：

var maze = new Maze(column, row, canvas); 
Module.addOnInit(function(){ 
    var ptr = Module._Maze_generate(column, row); 
    maze.linkedMap = readInt32Array(ptr, column * row); 
    maze.draw(); 
}); 

有兩種方法可以得到導出的函數，一種是在函數名前面加_，如Module._Maze_generate，第二種是使用它提供的ccall或cwrap函數，如ccall：

var linkedMapPtr = Module.ccall("Maze_generate", "number",  
                ["number", "number"], [column, row]); 

***個參數表示函數名，第二個返回類型，第三個參數類型，第四個傳參，或者用cwrap：

var mazeGenerate = Module.cwrap("Maze_generate", "number",  
                        ["number", "number"]); 
var linkedMapPtr = mazeGenerate(column, row); 

三種方法都會返回linkedMap的指針地址，可通過Module.get得到地址里面的值，如下代碼所示：

function readInt32Array(ptr, length) { 
    var linkedMap = new Array(length); 
    for(var i = 0; i < length; i++) { 
        var subptr = Module.getValue(ptr + (i * 4), 'i32'); 
        var neiborcells = []; 
        for(var j = 0; j < 4; j++){ 
            var value = Module.getValue(subptr + (j * 4), 'i32'); 
            if(value !== -1){ 
                neiborcells.push(value, 'i32'); 
            } 
        } 
        linkedMap[i] = neiborcells; 
    } 
  return linkedMap; 
} 

由于它是一個二維數組，所以數組里面存放的是指向數組的指針，因此需要再對這些指針再做一次get操作，就可以拿到具體的值了。如果取出的值是-1則表示不是有效的相鄰元素，因為C里面數組的長度是固定的，無法隨便動態push，因此我在C里面都初始化了4個，因為相鄰元素最多只有4個，初始時用-1填充。取出非-1的值push到JS的數組里面，得到一個用WASM計算的linkedMap. 然后再用同樣的方法去畫地圖。

***再比較一下WASM和JS生成迷宮的時間。如下代碼所示，運行50次：

var count = 50; 
console.time("JS generate maze"); 
for(var i = 0; i < count; i++){ 
    var maze = new Maze(column, row, canvas); 
    maze.generate(); 
} 
console.timeEnd("JS generate maze"); 
  
Module.addOnInit(function(){ 
    console.time("WASM generate maze"); 
    for(var i = 0; i < count; i++){ 
        var maze = new Maze(column, row, canvas); 
        var ptr = Module._Maze_generate(column, row); 
        var linkedMap = readInt32Array(ptr, column * row); 
    } 
    console.timeEnd("WASM generate maze"); 
}) 

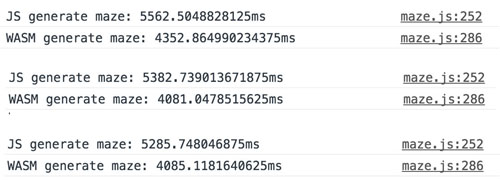
迷宮的規模為50 * 50，結果如下：

可以看到，WASM的時間大概快了25%，并且有時候會觀察到WASM的時間甚至要比JS的時間要長，這時因為算法是隨機的，有時候拆掉的墻可能會比較多，所以偏差會比較大。但是大部份情況下的25%還是可信的，因為如果把隨機選取的墻保存起來，然后讓JS和WASM用同樣的數據，這個時間差就會固定在25%，如下圖所示：

這個時間要比上面的大，因為保存了一個需要拆的墻比較多的數組。理論上不用產生隨機數，時間會更少，不過我們的重點是比較它們的時間差，結果是不管運行多少次，時間差都比較穩定。

所以在這個例子里面WASM節省了25%的時間，雖然提升不是很明顯，但還是有效果，很多個25%累積起來還是挺長的。

綜上，本文用JS和WASM使用連通集算法生成迷宮，并用最短路徑算法求解迷宮的路徑。使用WASM在生成迷宮的例子里面可以提升25%的速度。

雖然迷宮小時候就已經在玩了，不是什么高大上的東西，但是通過這個例子討論到了一些算法，還用到了很出名的最短路徑算法，還把WASM實際地應用了一遍，作為學習的的模型還是挺好的。更多的算法可參考這篇《我接觸過的前端數據結構與算法》。

【本文是51CTO專欄作者“人人網FED”的原創稿件，轉載請通過51CTO聯系原作者獲取授權】

戳這里，看該作者更多好文