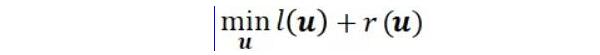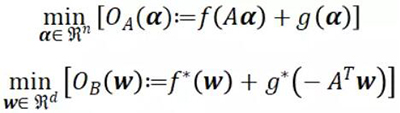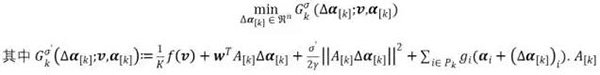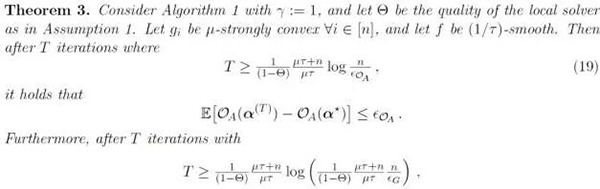去年，Michael I. Jordan 實(shí)驗(yàn)室發(fā)表論文《CoCoA: A General Framework for Communication-Efficient Distributed Optimization》提出了一種用于機(jī)器學(xué)習(xí)的分布式優(yōu)化的通用框架 CoCoA。機(jī)器之心技術(shù)顧問(wèn) Yanchen Wang 對(duì)該研究進(jìn)行了深度解讀。

一、引言

在做深度學(xué)習(xí)時(shí)，現(xiàn)代數(shù)據(jù)集的規(guī)模必需高效的設(shè)計(jì)和開(kāi)發(fā)，而且理論上算法也要進(jìn)行分布式優(yōu)化。分布式系統(tǒng)可以實(shí)現(xiàn)可擴(kuò)展性——不管是垂直擴(kuò)展還是水平擴(kuò)展，提升計(jì)算和存儲(chǔ)能力;但同時(shí)也讓算法設(shè)計(jì)者面臨著一些獨(dú)特的難題。其中一個(gè)尤其關(guān)鍵的難題是在機(jī)器學(xué)習(xí)負(fù)載的背景下，開(kāi)發(fā)能有效地協(xié)調(diào)機(jī)器之間的通信的方法。對(duì)大多數(shù)生產(chǎn)集群而言，網(wǎng)絡(luò)通信確實(shí)比單臺(tái)工作機(jī)器上的本地內(nèi)存存取要慢得多;但是，擴(kuò)展單臺(tái)機(jī)器顯然不可行。這個(gè)問(wèn)題還可以更加復(fù)雜，本地計(jì)算和遠(yuǎn)程通信之間的***平衡取決于數(shù)據(jù)集的特定屬性(比如維度、數(shù)據(jù)點(diǎn)的數(shù)量、稀疏度、偏度等)、分布式系統(tǒng)的特定屬性(比如數(shù)據(jù)存儲(chǔ)格式、分布式方案和數(shù)據(jù)存取模式等邏輯方面的設(shè)計(jì)，以及網(wǎng)絡(luò)層次結(jié)構(gòu)、帶寬、計(jì)算實(shí)例規(guī)范等物理方面的條件)和負(fù)載的特定屬性(比如簡(jiǎn)單的 ETL 過(guò)程肯定不同于 logistic 回歸的迭代式擬合)。因此，算法設(shè)計(jì)者必須要讓他們的優(yōu)化/機(jī)器學(xué)習(xí)算法具有足夠的靈活性，從而在保證快速收斂的前提下實(shí)現(xiàn)特定分布式系統(tǒng)的「計(jì)算-通信」的***平衡。

CoCoA 是加州大學(xué)伯克利分校 Michael I. Jordan 的實(shí)驗(yàn)室最近提出的一個(gè)框架，通過(guò)對(duì)多種多樣的優(yōu)化問(wèn)題的智能分解而實(shí)現(xiàn)了上述目標(biāo)。通過(guò)自由選擇原始或?qū)ε嫉哪繕?biāo)來(lái)解決，該框架成功利用了凸對(duì)偶性(convex duality)，從而可將全局問(wèn)題分解成一攬子可在工作機(jī)器上有效并行求解的子問(wèn)題，并且可以將局部更新組合起來(lái)以一種可證明的方式確保快速全局收斂。CoCoA 有兩個(gè)顯著優(yōu)勢(shì)：1)在每臺(tái)工作機(jī)器上都可以最有效地運(yùn)行任意本地求解器;2)計(jì)算-通信的權(quán)衡可以作為形式化問(wèn)題的一部分進(jìn)行調(diào)節(jié)，因此可以對(duì)每個(gè)不同的問(wèn)題和數(shù)據(jù)集進(jìn)行有效的調(diào)節(jié)。

根據(jù)數(shù)據(jù)在分布式集群上的分布情況(不管是根據(jù)特征還是根據(jù)數(shù)據(jù)點(diǎn))，CoCoA 可以將全局問(wèn)題分解成近似的局部子問(wèn)題，推薦應(yīng)求解原始目標(biāo)或是對(duì)偶目標(biāo)。每個(gè)子問(wèn)題都使用當(dāng)前***的現(xiàn)成單臺(tái)機(jī)器求解器解決，然后在單一一步 REDUCE 步驟中將來(lái)自每次迭代的局部更新組合起來(lái)(REDUCE 這個(gè)術(shù)語(yǔ)借用自 MAP-REDUCE)。實(shí)驗(yàn)表明 CoCoA 可以在 SVM、線性/logistic 回歸和 lasso 算法上實(shí)現(xiàn)*** 50 倍的加速。

在這篇報(bào)告中，我們將了解 CoCoA 的核心思想和最重要的結(jié)論，感興趣的讀者可以在參考文獻(xiàn)中找到詳細(xì)論證和更多實(shí)驗(yàn)。本報(bào)告的目標(biāo)是啟發(fā)我們分布式機(jī)器學(xué)習(xí)領(lǐng)域的讀者以及邀請(qǐng)更多人加入到我們的討論中，與我們交流知識(shí)以及為我們的技術(shù)社區(qū)做出貢獻(xiàn)。

二、問(wèn)題設(shè)置

CoCoA 的目標(biāo)是解決機(jī)器學(xué)習(xí)算法中普遍存在的下面一類(lèi)優(yōu)化問(wèn)題：

其中 l 和 r 是向量變量 u 的凸函數(shù)。在機(jī)器學(xué)習(xí)領(lǐng)域，l 通常是一個(gè)單獨(dú)的函數(shù)，表示所有數(shù)據(jù)點(diǎn)的經(jīng)驗(yàn)損失(empirical loss)的總和;而，表示 p 范數(shù)的正則化項(xiàng)。SVM、線性/logistic 回歸、lasso 和稀疏 logistic 回歸都屬于這個(gè)類(lèi)別。這個(gè)問(wèn)題通常是在原始空間或?qū)ε伎臻g解決的。在我們的討論中，我們將這種原始/對(duì)偶問(wèn)題抽象成了下面的 Fenchel-Rockafeller 對(duì)偶形式：

其中 α 和 w 是原始/對(duì)偶變量，A 是包含數(shù)據(jù)點(diǎn)列向量的數(shù)據(jù)矩陣，而 f* 和 g* 則是 f 和 g 的凸共軛。非負(fù)的對(duì)偶間隙(duality gap)，其中 w(α)=∇f(Aα)，為原始或?qū)ε嫉拇蝺?yōu)性(suboptimality)提供了一個(gè)可計(jì)算的上限，并且可以在強(qiáng)凸性下在***解點(diǎn)減少到零。它可以用于驗(yàn)證解的質(zhì)量和用作是否收斂的標(biāo)志。根據(jù) l 的平滑度和 r 的強(qiáng)凸性，我們可以將目標(biāo) l(u)+r(u) 映射到 OA 或 OB：

每種情況的典型案例有：彈性網(wǎng)絡(luò)回歸是 Case I，lasso 是 Case II，SVM 是 Case III。這里省略了推倒過(guò)程。

三、CoCoA 框架

要在數(shù)據(jù)分布在 K 臺(tái)機(jī)器上時(shí)最小化目標(biāo) OA，我們需要將計(jì)算分配給 K 個(gè)局部子樣本并在每次全局迭代過(guò)程中將 K 個(gè)局部更新組合起來(lái)。首先將數(shù)據(jù)矩陣 A 的列分成 K 個(gè)數(shù)據(jù)分區(qū)。對(duì)于每個(gè)工作機(jī)器 k，定義，其中當(dāng) i∈Pk 時(shí)，，否則。注意這種表示方式與數(shù)據(jù)的分布方式無(wú)關(guān)——數(shù)據(jù)矩陣的維度 n 和 d 各自都可以表示特征的數(shù)量或數(shù)據(jù)點(diǎn)的數(shù)量。這種可互換性是 CoCoA 的一個(gè)顯著優(yōu)勢(shì)——提供了靈活的數(shù)據(jù)分區(qū)方式，通過(guò)特征或數(shù)據(jù)點(diǎn)都可以，這取決于哪個(gè)更大以及使用了哪種算法。

分布 g(α) 很簡(jiǎn)單，因?yàn)樗强煞值?a target="_blank">;但要分布 f(Aα)，我們需要最小化它的二次近似。我們定義了以下僅讀取局部數(shù)據(jù)子樣本的局部二次子問(wèn)題：

表示機(jī)器 k 上的一組列，類(lèi)似于是來(lái)自前一次迭代的共享向量，表示局部變量αi 在所有 i∈Pk 上的變化，而且在 i∉Pk 時(shí)為零。這個(gè)子問(wèn)題是圍繞固定的 v 的臨近區(qū)域 f 的線性化，可以通過(guò)大多數(shù)有效的二次優(yōu)化求解器解出。可以直觀地看到，試圖隨局部變化而非常近地近似全局目標(biāo) OA。如果每個(gè)局部子問(wèn)題都可以得到***解，那么 REDUCE K 個(gè)更新可以被解讀成一個(gè)獨(dú)立于數(shù)據(jù)的、與數(shù)據(jù)塊無(wú)關(guān)的近似 OA 的 f 部分的步驟。但是，和傳統(tǒng)的近似方法不同，CoCoA 并不需要***的局部解。相反，它容許局部次優(yōu)性(定義為與***的期望絕對(duì)偏差)，并且會(huì)將其整合進(jìn)自己的收斂邊界中，下面就可以看到。有些實(shí)踐者想復(fù)用已有的針對(duì)特定問(wèn)題、數(shù)據(jù)集和機(jī)器配置優(yōu)化的單個(gè)求解器，對(duì)于他們而言，這是一個(gè)巨大的優(yōu)勢(shì)。

完整算法如下：

其中有兩個(gè)可調(diào)節(jié)的超參數(shù)：γ 控制了工作機(jī)器的更新的組合方式，σ' 則表示數(shù)據(jù)分區(qū)的難度。實(shí)際上，對(duì)于一個(gè)給定的 γ∈(0,1]，我們?cè)O(shè) σ':=γK。γ=1 且 σ'=K 能保證最快的收斂速度，盡管理論上任何都應(yīng)該是足夠的。詳細(xì)證明請(qǐng)參閱原論文。

CoCoA 的原始-對(duì)偶靈活性是一大主要優(yōu)勢(shì)。盡管事實(shí)上我們一直都在求解 OA，但我們可以自由地把它看作是的原始或?qū)ε?mdash;—如果我們將這個(gè)原始問(wèn)題映射成了 OA，那么 OA 就是原始;如果我們將其映射成了 OB，那么 OA 就是對(duì)偶。將 OA 看作原始讓我們可以求解 lasso 這樣的非強(qiáng)凸性正則化項(xiàng)，通常這是當(dāng)數(shù)據(jù)按特征分布，而不是按數(shù)據(jù)點(diǎn)分布的時(shí)候。這能很好地適用于 lasso、稀疏 logistic 回歸或其它類(lèi)似 L1 的誘導(dǎo)稀疏性的先驗(yàn)(sparsity-inducing priors)。求解 CoCoA 的這種原始變體每次全局迭代的通信成本為 O(數(shù)據(jù)點(diǎn)的數(shù)量)。另一方面，將 OA 看作對(duì)偶讓我們可以考慮非平滑損失，比如 SVM 的 hinge loss 或絕對(duì)偏差損失，而且當(dāng)數(shù)據(jù)是按數(shù)據(jù)點(diǎn)而非特征分布時(shí)效果***。這種變體每次全局迭代的通信成本為 O(特征數(shù)量)。下面是對(duì)這兩種 CoCoA 變體的總結(jié)：

復(fù)用上面的表格，我們現(xiàn)在得到：

下表給出了在 CoCoA 框架中構(gòu)建的常見(jiàn)模型的例子：

在原始的設(shè)置(算法 2)中，局部子問(wèn)題變成了在局部數(shù)據(jù)塊上的二次問(wèn)題，其中僅有局部的是正則化的。在對(duì)偶的設(shè)置(算法 3)中，經(jīng)驗(yàn)損失僅應(yīng)用于局部，這使用了由一個(gè)二次項(xiàng)近似的正則化項(xiàng)。

四、收斂分析

關(guān)于收斂的詳細(xì)論證過(guò)于技術(shù)，會(huì)把我們的討論弄得比較混亂，為了避免這種情況，我們這里僅給出了關(guān)鍵結(jié)果。感興趣的讀者可以查看原始論文詳細(xì)了解。

為了簡(jiǎn)化我們的演示，這里給出了我們的三個(gè)主要假設(shè)：

1. 數(shù)據(jù)在 K 臺(tái)機(jī)器上均等分配;
2. 數(shù)據(jù)矩陣 A 的列滿足 ||xi||≤1;
3. 我們僅考慮 γ=1 且 σ'=K 的情況，這能保證收斂，而且在分布式環(huán)境中的收斂速度也最快。

我們的***個(gè)收斂結(jié)果涉及到使用一般凸性的 gi 或 L-Lipschitz 的(這兩個(gè)條件是等價(jià)的)：

其中 L-bounded support 和-smooth 的定義可以在原論文找到。這個(gè)定理涵蓋了帶有非強(qiáng)凸性正則化項(xiàng)(比如 lasso 和稀疏 logistic 回歸)的模型或帶有非平滑損失(比如 SVM 的 hinge loss)的模型。

我們還可以證明在強(qiáng)凸性的 gi 或平滑的(這兩個(gè)條件也是等價(jià)的)上有更快的線性收斂速度，這涵蓋了彈性網(wǎng)絡(luò)回歸和 logistic 回歸：

類(lèi)似地，μ-strong convexity 的定義也可以在原論文找到。

這兩個(gè)定理都參考了下列假設(shè)作為局部解 Θ 的質(zhì)量的定義。

這個(gè)假設(shè)基本上將 Θ 定義成了局部二次問(wèn)題的經(jīng)驗(yàn)絕對(duì)偏差之前的相乘的常數(shù)。實(shí)際情況下，并行地分配到局部計(jì)算的時(shí)間應(yīng)該差不多等于池化所有 K 個(gè)工作機(jī)器的更新的全部通信時(shí)間成本。

將這些收斂定理與我們前面的類(lèi)別關(guān)聯(lián)起來(lái)：

五、實(shí)驗(yàn)

我們將 CoCoA 與幾種適用于 lasso、彈性網(wǎng)絡(luò)回歸和 SVM 的當(dāng)前***的通用大規(guī)模分布式優(yōu)化算法進(jìn)行了比較：

1. MB-SGD：minibatch 隨機(jī)梯度下降。對(duì)于 lasso，我們?cè)?L1-prox 上與 MB-SGD 進(jìn)行了比較。我們?cè)?Apache Spark MLlib v1.5.0 中進(jìn)行了實(shí)現(xiàn)和優(yōu)化。
2. GD：完全梯度下降。對(duì)于 lasso，我們使用了近似版本 PROX-GD。我們?cè)?Apache Spark MLlib v1.5.0 中進(jìn)行了實(shí)現(xiàn)和優(yōu)化。
3. L-BFGS：有限內(nèi)存擬牛頓法。對(duì)于 lasso，我們使用了 OWL-QN(orthant-wise limited quasi-Newton method)。我們?cè)?Apache Spark MLlib v1.5.0 中進(jìn)行了實(shí)現(xiàn)和優(yōu)化。
4. ADMM：交替方向乘子法。對(duì)于 lasso，我們使用了共軛梯度;對(duì)于 SVM，我們使用了 SDCA(隨機(jī)對(duì)偶坐標(biāo)上升)。
5. MB-CD：minibatch 并行化的坐標(biāo)下降。對(duì)于 SVM，我們使用了 MB-SDCA。

為了避免麻煩，這些不談每種參與比較的方法的調(diào)參細(xì)節(jié)。感興趣的讀者可以參考原論文，以便重現(xiàn)論文的結(jié)果。對(duì)于 CoCoA，所有的實(shí)驗(yàn)在單機(jī)上都使用了隨機(jī)坐標(biāo)下降作為局部求解器。如果使用更加復(fù)雜的求解器，當(dāng)然有可能進(jìn)一步提升表現(xiàn)水平。這個(gè)開(kāi)放性的實(shí)踐就留給感興趣的讀者探索吧。

我們比較的指標(biāo)是離原始***(primal optimality)的距離。為此我們?yōu)樗蟹椒ǘ歼\(yùn)行了大量迭代次數(shù)，直到觀察不到明顯的進(jìn)展為止，然后選擇其中最小的原始值。使用的數(shù)據(jù)集是：

所有代碼都是用 Apache Spark 編寫(xiě)的，并且都運(yùn)行在 Amazon EC2 m3.xlarge 實(shí)例上(每臺(tái)機(jī)器一個(gè)核)。代碼已發(fā)布到 GitHub：

www.github.com/gingsmith/proxcocoa。

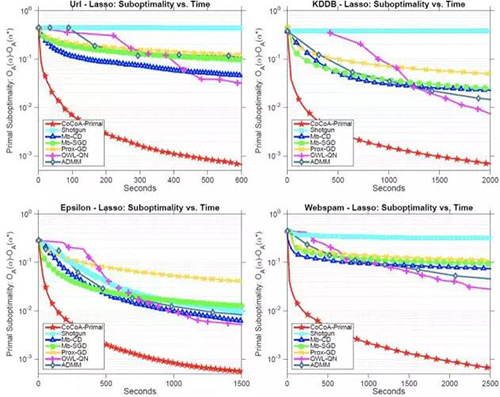
在原始的設(shè)置中，我們應(yīng)用 CoCoA 在上述每個(gè)數(shù)據(jù)集上擬合 lasso 模型，其中使用了隨機(jī)坐標(biāo)下降作為局部求解器，而總迭代次數(shù) H 調(diào)節(jié)了局部解的質(zhì)量 Θ。我們也包括了多核 SHOTGUN 作為極端案例。對(duì)于 MB-CD、SHOTGUN 和原始 CoCoA，數(shù)據(jù)集是按特征分布的;而對(duì)于 MB-SGD、PROX-GD、OWL-QN 和 ADMM，數(shù)據(jù)集則是按數(shù)據(jù)點(diǎn)分布的。以秒為單位繪制原始次優(yōu)性，我們得到：

很顯然，就算與比較中***的方法 OWL-QN 相比，CoCoA 的收斂速度也快了 50 多倍，而且在有大量特征的數(shù)據(jù)集上表現(xiàn)***，而這也正是 lasso 常常應(yīng)用的領(lǐng)域。

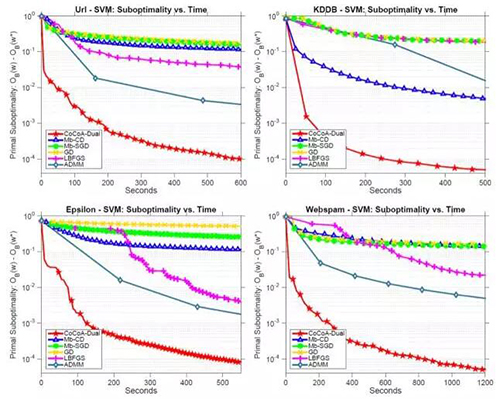
在對(duì)偶的設(shè)置中，我們考慮的是擬合 SVM。CoCoA 使用隨機(jī)對(duì)偶坐標(biāo)上升作為局部求解器。所有方法都按數(shù)據(jù)點(diǎn)分布數(shù)據(jù)。顯然，CoCoA 的表現(xiàn)又超出了其它方法一大截。

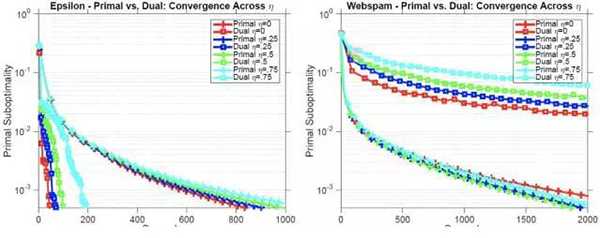
為了理解 CoCoA 的原始-對(duì)偶互換性，我們讓其兩種變體都擬合了彈性網(wǎng)絡(luò)回歸模型，并使用了坐標(biāo)下降作為局部求解器。

當(dāng)數(shù)據(jù)集有大量特征而非數(shù)據(jù)點(diǎn)時(shí)，原始 CoCoA 的表現(xiàn)更好，而且對(duì)強(qiáng)凸性的退化(deterioration)是穩(wěn)健的。另一方面，當(dāng)數(shù)據(jù)集有大量數(shù)據(jù)點(diǎn)而非特征時(shí)，對(duì)偶 CoCoA 的表現(xiàn)更好，在針對(duì)強(qiáng)凸性的損失的穩(wěn)健性方面不夠好。這提醒實(shí)踐者在面臨不同的問(wèn)題設(shè)置時(shí)，應(yīng)該使用不同的 CoCoA 變體——算法 2 或算法 3.

原論文還報(bào)告了更多有趣的發(fā)現(xiàn)，比如原始 CoCoA 可以保留局部稀疏性，并會(huì)將其最終傳遞為全局稀疏性;調(diào)節(jié)控制 Θ 的 H 允許機(jī)器學(xué)習(xí)系統(tǒng)設(shè)計(jì)者一路探索「計(jì)算-通信」權(quán)衡曲線，以確定他們當(dāng)前系統(tǒng)的***平衡所在。

六、總結(jié)

CoCoA 是一個(gè)通用分布式優(yōu)化框架，可以在分布式集群中實(shí)現(xiàn)通信高效的原始-對(duì)偶優(yōu)化。它的方式是利用對(duì)偶性將全局目標(biāo)分解成局部二次近似子問(wèn)題，而這些子問(wèn)題可以使用架構(gòu)師選擇的任意當(dāng)前***的單機(jī)求解器并行地求解到任意準(zhǔn)確度。CoCoA 的靈活性允許機(jī)器學(xué)習(xí)系統(tǒng)設(shè)計(jì)者和算法開(kāi)發(fā)者輕松探索分布式系統(tǒng)的「計(jì)算-通信」權(quán)衡曲線，并為他們的特定硬件配置和計(jì)算負(fù)載選擇***的平衡。在實(shí)驗(yàn)中，CoCoA 將這種選擇總結(jié)歸納成了單個(gè)可調(diào)的超參數(shù) H(迭代的總次數(shù))，它間接等效的 Θ(局部解的質(zhì)量)進(jìn)入了關(guān)于原始和對(duì)偶 CoCoA 的收斂速度的兩個(gè)重要理論證明。實(shí)證結(jié)果表明 CoCoA 的表現(xiàn)可以以*** 50 倍的差距超越當(dāng)前***的分布式優(yōu)化方法。

【本文是51CTO專(zhuān)欄機(jī)構(gòu)“機(jī)器之心”的原創(chuàng)文章，微信公眾號(hào)“機(jī)器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文