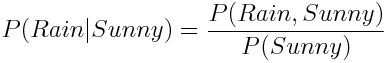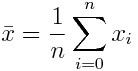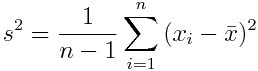學習機器學習前,你首先要掌握這些概率論基礎知識
機器學習中有很多十分重要的核心基礎概念,掌握這些概念對我們進行機器學習和數據科學的相關工作十分重要,可以幫助我們發現一些以往容易被忽視的新線索。那么其中很重要的一個就是——概率。
有的朋友在看見概率的時候可能會問,我們已經有了那么多很好用的數學工具了,為什么還需要概率呢?我們擁有可以解決多種尺度并衡量其變化的微積分;擁有可以借方程做變化的線性代數,還有很多很多的數學工具可以解決幾乎我們能想到的所有難題。概率似乎不是那么重要了?
但事實上,我們生活在一個充滿混沌和不確定的世界里,很多事情沒辦法精確的測量。當我們進行研究的時候,面對的是隨機誤差和不確定性的干擾。不確定性幾乎無處不在,我們需要了解它的習性,掌握并利用它,這就是我們需要概率理論和統計的原因。
- 如今概率已經深入到人工智能、粒子物理、社會科學、生物信息科學等方方面面,甚至我們日常生活中的點點滴滴。
- 概率和統計的概念如此重要,下面我們就為大家闡述概率相關的不同概率,希望大家可以對概率有更清晰的認識。
頻率論概率
想象一下我們要測量一個硬幣是否均勻,需要進行怎樣的實驗呢?我們需要不斷的拋硬幣,并記錄每一次的朝向,重復1000次后讓我們來看看實驗的結果。如果結果是600次朝上400 次朝下,那么我們將得到60%和40%的概率。這個概率就可以作為硬幣朝上或者朝下的概率,這樣的方式成為頻率派的概率觀點。
條件概率
頻率派的觀點需要通過大量實驗的記錄來總結。但條件概率卻是不一樣的觀點,在事件B發生的情況下A發生的概率。讓我們來看兩個例子:
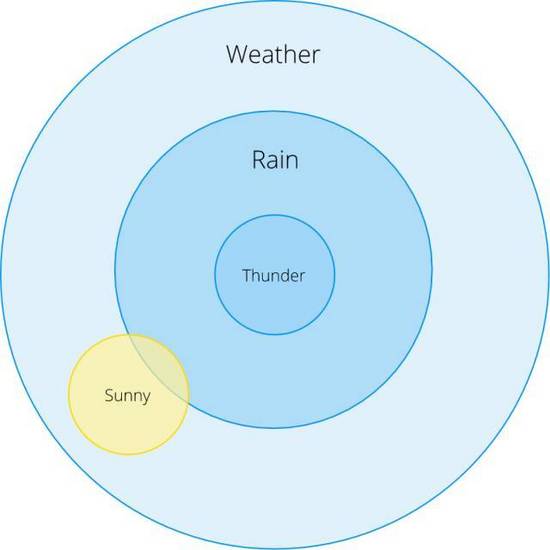
- 我們看到電閃雷鳴的情況下下雨的概率是多少?
- 艷陽天下雨的概率是多少?
在上面的歐拉圖中我們可以看大P(Rain | Thunder) = 1, 意味著打雷就會下雨(假定100%),但對于 P(Rain | Sunny)呢?雖然這個概率很小,但是我們如何通過一個公式將它表達出來呢?這就引出了條件概率的表達式:
我們通過將同時下雨和出太陽的概率除以出太陽的概率算出了出太陽的情況下會下雨的條件概率。
獨立和依賴事件
如果某一事件發生的概率完全不受到其他事件的影響,我們就稱其為獨立事件。 例如我們在拋色子是,***筆拋了2,第二次拋2 的概率,這兩次拋是獨立的,那么同時得到2 的概率可以寫為:
但是為什么上面的公式是對的呢?我們首先將***次和第二次拋色子事件分別寫成A和B,并將同時得到2 的概率寫成事件A和B的聯合概率分布:
這時在等式兩邊除以P(B)并利用條件概率的定義我們得到下面的式子:
我們發現 P(A | B) = P(A)。這意味著A與B是相對獨立的,B的發生對A并不造成任何影響。
貝葉斯概率
頻率派一般會利用統計的方法找出與模型的參數,而貝葉斯理論則認為模型的參數也滿足一定的分布。在貝葉斯統計中,每一個參數擁有自己的統計分布,在一定的數據下給出參數的可能性的分布:
這一公式的基礎就是上面提到的條件概率:
盡管表達式十分簡單,但是貝葉斯理論十分強大,廣泛應用在各個學科,甚至產生了一門稱為貝葉斯統計的統計學分支。如果你對貝葉概率感興趣,下面這個博客是不錯的學習資料:https://www.countbayesie.com/blog/2015/2/18/bayes-theorem-with-lego
分布
有的小伙伴又會問了,貝葉斯概率很好,那到底什么是分布呢?分布其實是一個描述某一個量不同取值范圍及其概率的(實驗或者數學推導)函數,在函數中有一些參數可以調整這一分布的行為(范圍和取值概率)。
當我們測量硬幣正反的時候得到了一個分布,這稱之為經驗的概率分布。在現實生活中,很多類似事情是可以通過概率分布來描述的。例如拋硬幣實驗就滿足伯努利分布,并可以利用這個分布來計算n次實驗后哪一面朝上的概率。
在概率論中,還需要明確一個稱為隨機變量的概念。每一個隨機變量都有自己的分布,我們一般約定俗成的將隨機變量寫成大寫字母來表示,并用~來表示其所屬的分布:
上式意味著隨機變量X滿足0.6的伯努利分布。
連續和離散分布
概率分布一般分為兩種情況:離散分布和連續分布。離散分布是指隨機變量只在一些有限的位置取值,例如拋硬幣的伯努利分布,離散分布一般利用概率質量函數Probability Mass Functions (PMF) 來定義;而連續分布一般用來處理無窮多個隨機變量取值的情況。例如測量帶有噪音的速度就是一個連續分布的例子。連續分布一般利用概率密度函數Probability Density Functions (PDF) 來定義。
對應的概率離散利用連加∑ 符號,連續概率利用∫符號來描述。
樣本和統計
想象一下我們想要進行一個人體身高的測量研究,我們在大街上隨機的測量了一些陌生人的身高,那么這個測量可以看做是獨立的。我們將從一個人群中隨機選取樣本的過程稱為采樣。統計的作用就是對這些數據進行總結和信息的提取,例如計算這些樣本的均值:
樣本的標準差是這樣計算的:
這一公式用來描述數據點與其均值的偏差。
更多的進階學習
學了這么多感覺不錯吧?你一定想要進行更深入的學習吧!這些知識一定會讓你在日后的研究工作中受益,并收獲更深的理解。
- 入門級:Khan Academy很不錯,深入淺出的講解了很多相關的基礎知識。https://www.khanacademy.org/math/statistics-probability
- 進階級:All of the Statistics是一個簡潔的教程,包含了統計學的重要知識點,但需要注意的是你需要線性代數和微積分的基礎知識才能順利的完成學習。https://www.amazon.com/All-Statistics-Statistical-Inference-Springer/dp/0387402721
希望你在概率中發現更多的美,能在自己的學習工作熟練的應用相關的思想,做出更好的成績。