「多體問題」（又叫 N 體問題）是看似簡單，實際上在當今數學中極難攻克的問題。多體問題是指多個相互作用的實體。在物理學中，任何三體問題都沒有一個封閉的形式或解析解（見：https://en.wikipedia.org/wiki/Three-body_problem）。像這樣簡單的問題反映了我們分析工具的局限性。這并不意味著它是不可解的，它只意味著我們必須訴諸于近似和數值技術來進行計算。可以用足夠精確的數值計算分析太陽、月球和地球之間的三體問題以幫助宇航員登陸月球。

在深度學習領域，我們也有一個新興的 N 體問題。許多更先進的系統現在正在處理多代理系統的問題。每個代理都可能有與全局目標合作或競爭的目標（即目標函數）。在多代理深度學習系統中，甚至在模塊化的深度學習系統中，研究人員需要設計可擴展的合作方法。

Johannes Kepler 大學、DeepMind、OpenAI 和 Facebook 最近紛紛發表論文探討了這個問題的各個方面。

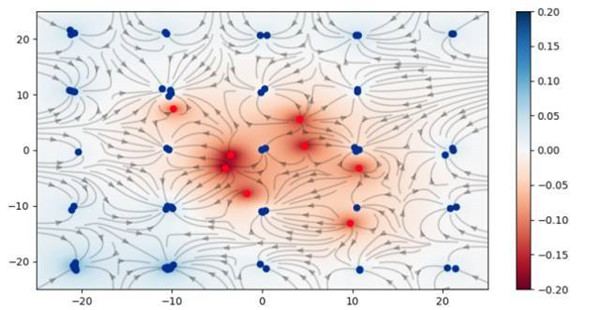
在 Johannes Kepler 大學的團隊，包括 Sepp Hochreiter（LSTM 的提出者）已提出利用模擬庫侖力（即電磁力大小與反向距離的平方成比例）作為一種訓練生成對抗網絡（GAN）的替代目標函數。

找到兩個對抗網絡之間的平衡狀態是一個熱門的研究課題。在深度學習中解決二體問題相當困難。研究發現，使用這種方法可以防止「模式崩潰」的不良情況。此外，設置確保收斂到一個***的解決方案，而且只有一個恰好也是全局的局部極小值。Wasserstein 目標函數（又名 Earth Mover Distance）可能是一個更好的解決方案，這在幾個月前極其熱門。這個團隊已經把他們的創造命名為「庫侖 GAN」。

微軟 Maluuba 發表了一篇論文介紹了一個人工智能玩吃豆人游戲的系統，它的水平已經超過了人類。研究人員挑戰的吃豆人游戲跟此類游戲最初的版本類似，人物在收集小球和水果的同時避免怪物。論文的題目是「強化學習的混合式獎勵架構」。本文介紹了不同于典型的強化結構的強化學習（RL）的實現（即 HRA）：

這篇文章令人驚訝的是所使用的目標函數的數量。本文描述了使用 1800 值函數作為其解決方案的一部分，也就是說，每個小球、每個水果和每個怪物都使用了代理。微軟的研究表明使用數以千計的微型代理將問題分解成子問題并實際解決它是有效的！在這個模型中，代理之間的耦合顯然是隱式的。

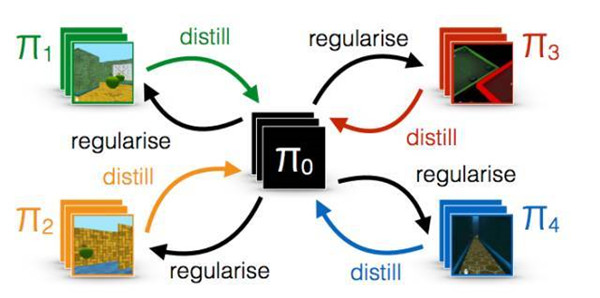
DeepMind 解了具有共享內存的多代理程序的問題。在論文《Distral: Robust Multitask Reinforcement Learning》中，研究人員通過「思想融合」靈感的代理協調方法來解決一個共同的問題。為此，研究人員采用了一種封裝每個代理的方法。然而，它們允許一些信息通過代理的封裝邊界，希望狹窄的通道更具伸縮性和魯棒性。

我們提出了多任務聯合訓練的新方法，我們稱之為 distral（提取和遷移學習）。我們不建議在不同的網絡之間共享參數，而是共享一個「提取」的策略，以捕獲跨任務的共同行為。每個網絡都被訓練用來解決自己的任務，同時受限于近似共享的策略，而共享策略通過提取訓練成為所有任務策略的中心。

其結果引出了更快，更穩定的學習，從而驗證了狹窄通道的方法。在這些多代理（N 體問題）開放性問題是這種耦合的本質。DeepMind 的論文表明了更低的耦合相對于原生的緊耦合的方法的有效性（即權重共享）。

OpenAI 最近發表了在他們的系統中訓練模型匹配其他代理的多系統的有趣的論文。論文題目為《Learning with Opponent-Learning Awareness》。該論文表明，「以牙還牙」戰略的出現源自賦予多代理系統社會意識能力。盡管結果具有彈性問題，但它確實是一種非常令人著迷的方法，因為它解決了人工智能的一個關鍵維度（參見：多維智能）。

總而言之，許多領先的深度學習研究機構正在積極探索模塊化深度學習。這些團體正在探索由不同的對象函數組成的多代理系統，所有這些都用于合作解決單一的全局目標函數的。仍然有許多問題需要解決，但顯然，這種做法確實非常有希望取得進展。去年，我發現博弈論的變化對未來進步***指導意義。在今年，我們將看到更多探索多代理系統的松散耦合嘗試。