本文摘自Logan Brutsche的圖書《The Layman's Guide to Bitcoin》。

密碼學是應用數學函數以保證數據安全性的科學。

許多風靡的影視作品都在向人們暗示：只要有足夠厲害的黑客，任何系統都可以被攻破。這種“好萊塢式黑客攻擊”并不是真實世界的場景——黑客必須發現系統暴露的漏洞，例如未上鎖的服務器機房、易于猜測的密碼、未受保護的網絡端口或者內部安裝的“后門”，以進而實現未經授權的訪問。

雖然我們的確永遠無法確保一個系統沒有任何漏洞——畢竟系統都是由不完美的人類所完成的，但是“任何系統都可以被攻破”這一觀點卻是錯誤的。自90年代初以來，我們利用密碼技術已經可以實現完全免受黑客攻擊。但這一技術在應用時有時會留下被黑客利用的空間。

密碼學本身并不會被黑客攻破以生成偽造的數字簽名（馬上會給出定義），就像數學不能被黑客攻擊而使得2+2=5一樣——雖然密碼學和數學都可能被錯誤地使用。如果一個使用密碼學的系統被攻破，那只可能是因為設計者錯誤地應用了密碼學。這不是因為密碼學不起作用，也不是因為有人“破解”了密碼學——就像你的銀行錯誤地處理了你的賬戶時不是數學的錯誤、你的媽媽下載不熟悉的附件而感染計算機病毒時不是電子郵件的錯誤一樣。這是一個很重要的特點，因為比特幣是一個非常直接的密碼學應用。

密碼學并不是一種未經考驗的新技術。比特幣所使用的所有密碼學技術自互聯網誕生以來一直都在使用著，是每天使用的許多常見互聯網協議的重要部分。計算機科學家認為密碼學是可靠和必要的，就像NASA（美國國家航空航天局）認為宇航科學是可靠和必要的一樣。

公私鑰對：密碼學的基石

公私鑰對是區塊鏈所使用密碼學的基石。公私鑰對包含兩部分：私鑰和公鑰。這兩個密鑰實際上只不過是具有特定數學關系的大整數，用于代替密碼和用戶名。 

你會擁有一個公鑰，就像你的名字或用戶名一樣：在大多數情況下，你可以向任意請求者分享你的公鑰，而擁有它的人可以用它來引用或聯系你。它與你的名聲（或者比特幣中你的交易歷史）綁定，所以你可能會有多個公鑰（因此有多個公私鑰對）用于不同的目的。公鑰可用于引用或查看帳戶，但它自身并不能對該帳戶作任何操作。

私鑰應該像密碼一樣：不應向任何人分享，它用于驗證某些操作，例如發送BTC（比特幣）。

但是私鑰和密碼之間存在重要的區別。要使用密碼，你必須將其發送給某個人或服務器，以便其對密碼進行驗證。你需要相信密碼在發送后會被負責任地處理。相比之下，私鑰可用于證明自己的身份而無需將其發送給任何人。它曾經存儲或直接使用過的唯一場所就是在你的本地設備上。

這一點很重要，因為如果你可以在不向任何人發送你的秘密信息的情況下對自己進行身份認證，則可以保證完全控制其安全性——你不易受其他系統的安全漏洞影響。這是使比特幣不可撼動的重要組成部分。比特幣本身并沒有存儲可能泄露給攻擊者的密碼或私鑰，但用戶仍然可以對交易進行驗證。

但是，如果你從來不曾向任何人發送私鑰，那么如何使用私鑰來驗證交易呢？答案與私鑰和公鑰之間的數學關系有關：數字簽名。

數字簽名

有許多種不同的生成和驗證數字簽名的技術，支撐它們工作的數學原理遠遠超出了本文的范疇。對于那些不熟悉密碼學的人來說，這里所描述的過程最初聽起來可能令人難以置信。我很清楚地記得，當我四年前剛開始研究比特幣的時候就有過這樣的感覺。

現在我將再次簡要提到，這些技術被用于許多常見的互聯網協議中，并且是信息科學的既有組成部分。

想象有Alice和Bob兩個人，他們已經在私下交換了公鑰。Alice想給Bob發送一條消息，但Bob是一個非常多疑的人，除非他能夠以數學的方式進行確定性地證明，否則他不相信該消息確實來自Alice。為了便于證明，他們同意使用數字簽名。

為了生成簽名，Alice使用她計算機中的簽名生成算法，該算法將她的私鑰和完整的消息作為輸入，生成一個數字簽名。然后，她將這個消息/簽名組合發送給Bob——但重要的是，她不會發送她的私鑰。

當Bob收到消息和簽名時，他可以調用一個與之互補的簽名驗證算法。該算法將消息和簽名作為輸入，以確定Alice用于生成簽名所使用公私鑰對中的公鑰。當Bob看到他的算法輸出Alice的公鑰時，他就已經在數學上證明了該簽名確實是用Alice的公私鑰對生成的，即使他不知道也無法計算Alice的公私鑰對中的私鑰。

更簡潔地說，這一數字簽名的過程允許Bob驗證該消息不是由某個第三方創建或修改，而是必須使用Alice的私鑰才能生成的，而不必（或不能）知道她的私鑰。他需要的只有消息/簽名組合和她的公鑰。

直覺上來看，這似乎難以置信，你可能會覺得好像在哪里產生了誤解。如果Alice的私鑰和公鑰密切相關，并且Alice使用她的私鑰生成Bob收到的簽名，那他為什么只能派生出她的公鑰而得不到她的私鑰？要理解這一問題的答案要求比大多數人對數學更深入的理解，這遠遠超出了本書的范圍。

盡管如此，這項技術每天都在被賴以使用，并且在密碼學社區內被認為是堅如磐石的。當你訪問某個地址以https開頭的網站時，“s”就表示該網站使用數字簽名認證了它自己。你的計算機使用了簽名驗證算法，就像上面例子中的Bob一樣，驗證網站確實來自正確的公私鑰對。數字簽名可以確保你和網站之間的任何進一步交互都是經過加密和認證的。如果驗證失敗，瀏覽器則會警告你，并將該網站標記為危險。

足夠大的整數

在此之前，我簡單地提到了私鑰和公鑰的功能就像用戶名和密碼一樣，但實際上它們只不過是具有特殊數學關系的大整數。鑒于此，我經常被問到以下問題：

“能不能使用計算機猜測或者計算出一堆數字，并嘗試將它們作為私鑰使用？他們最終是否會碰到某個目標公私鑰對的私鑰，從而獲得對該身份的控制權？”事實上，就比特幣而言，這將使攻擊者可能竊取一些公私鑰對所持有的比特幣。

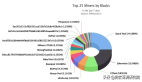
這是一個很好的問題，但它并不會發生。如前所述，有幾個擁有價值數百萬美元BTC的比特幣地址，但它們好幾年一直都沒有被轉移——盡管盜取它們需要的只是正確的私鑰——也就是正確的大整數！如果你能猜到這些地址的私鑰，那么你就可以將其中的錢發送給任何人。與密碼不同，你可以在自己的機器上本地驗證私鑰，沒有服務器會限制你的嘗試次數或頻率。

那為什么還沒有人偷​​走這些錢呢？答案在于用作私鑰的數字近乎荒謬的大小。它們足夠大。

我們從一個簡單的思維實驗開始。想象一下，你的私鑰足夠大，大到世界上所有的計算機一起工作，他們需要24小時才能猜到。如果在你的私鑰上增加僅僅一位數字，計算機就需要十倍的計算量，也就是需要十天而不是一天。而增加六位數字會使這一時間達到27000年。

在任何情況下，生成私鑰所需創建隨機數的計算能力都是微不足道的。使用私鑰生成簽名以及使用公鑰驗證這些簽名在計算上也是簡單的。但猜測私鑰所需的工作量卻隨著每添加一個額外數字呈指數增長。為了使私鑰“免疫”于暴力破解，我們只需要添加足夠的數字——我們只需要使它們足夠大。

那多大是足夠大？比特幣中使用的私鑰是256比特的整數，相當于一個長度為76位的數字。這一數字的大小是令人難以置信的。接下來的闡釋大部分來自于Bruce Schneier的圖書《Applied Cryptography（應用密碼學）》，對足夠大整數進行直觀說明。

首先，需要了解到熱力學第二定律的一個具體結論是改變單個二進制位信息存在所需要的最小能量（將1變為0或反之）。這意味著無論所使用的硬件如何，任何計算過程都需要一些最小的能量來執行。

現在假設你能夠利用太陽的全部能量輸出來驅動一臺專門設計的計算機，這臺計算機的工作是計算或猜測私鑰，以找到一個公私鑰對的私鑰（可以控制BTC）。

使用一點點數學和熱力學，你會發現一臺具有太陽全年能量輸出計算能力的高效計算機可以計算出$2^{178}$個值。如果我們將這個值除以可能的私鑰數量，即$2^{256}$，我們發現這個擁有太陽全年能量輸出計算能力的假想計算機只能猜測或計算出可能私鑰總數的0.0000000000000000000003％。

此外，這還只是計數，并不包括實際檢驗每個私鑰以驗證它是否與正確的公鑰對應這一更復雜的任務。因此，這臺計算機在一年之內可能錯過這0.0000000000000000000003％概率的正確私鑰，而它甚至都不會意識到。

這些數字與設備的技術無關; 它們是根據20世紀30年代以來建立的熱力學定律所得出的可能達到的最大值。這些數字意味著對256位密鑰（比特幣使用的密鑰）的暴力攻擊將是不可行的，除非計算機是由物質以外的東西構建并占用空間以外的東西。

這就是足夠大整數的能力。無論黑客有多厲害，除非他能夠利用$3\times {10}^{23}$個太陽的能力計算一年，或者一個太陽的能力計算$3\times {10}^{23}$年，否則他的電腦甚至無法完成對所有私鑰的計數——更不用說測試或者以其他方式使用它們了。

想要更深入地了解比特幣和密碼學，請閱讀Logan Brutsche的圖書《The Layman's Guide to Bitcoin》。

原文鏈接：https://cloud.tencent.com/developer/article/1051580

【本文是51CTO專欄作者“云加社區”的原創稿件，轉載請通過51CTO聯系原作者獲取授權】

戳這里，看該作者更多好文