今天聊聊關于對稱加密算法中關于密鑰的問題。如果對于密碼學的基礎概念還不太熟悉的可以復習一下我上一篇文章。手把腳看看密碼學No.72。

[[224482]]

我們都知道對稱密鑰可以用于傳送加密信息，過程是這樣的。

從上面的過程我們可以看到，如果傳送者跟接收者都有密鑰 KEY ，那么就可以在不安全的信道下進行安全的通信了，目前比較流行的對稱加密算法有 AES、DES、3DES、TDEA、Blowfish、RC5、IDEA等算法。。

那么問題來了，傳送者和接受者雙方都需要擁有同一個密鑰，那么這個過程要怎么實現呢？現實中我們可以這樣做，把一個鑰匙做兩份，然后裝在信封里邊面對面交易，拿到信封后回到家里鎖起房門蓋上被子打開手電筒偷偷摸摸看看密鑰然后記在腦海里，這樣就幾乎沒人可以偷走了吧？

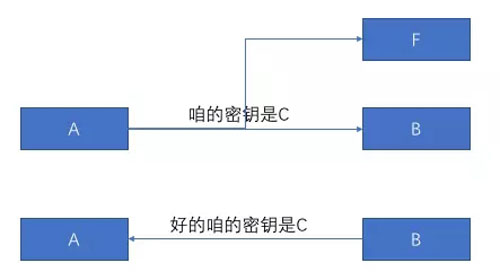
理想的情況應該是這樣的：

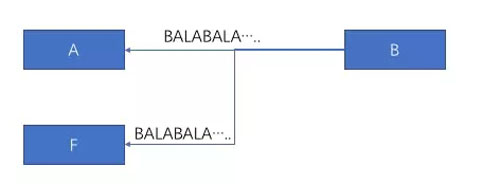
但是在網絡世界中，基本一切都是不安全的，可能會出現搞壞的的人，比如出來了一個叫F的人，在中途截獲了密鑰，那么A和B后面所有的交流都會被監聽了。

喏你看，一切消息都被破譯了吧，這時候 A 跟 B 之間的這個密鑰有跟沒有是一樣一樣一樣的。

那么究竟要怎么辦呢？這時候我們又要搬出偉大的數學了，今天介紹一種算法 迪菲－赫爾曼密鑰交換，這個算法能夠解決在不安全的信道下進行安全的密鑰交換問題，究竟是怎么實現的呢。

迪菲－赫爾曼密鑰交換（Diffie–Hellman key exchange，簡稱“D–H”） 是一種安全協議。它可以讓雙方在完全沒有對方任何預先信息的條件下通過不安全信道建立起一個密鑰。這個密鑰可以在后續的通訊中作為對稱密鑰來加密通訊內容。

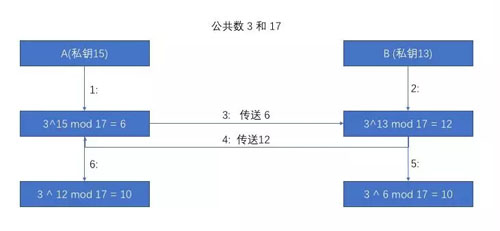
 主要的思路就是，根據數學的指數運算的法則來進行本地的計算（本地計算可以認為是安全的），同時用使用模運算來降低傳輸的數的值。算法的大概流程像下面的圖這樣。

首先確定一個公共的數對 （3 和 17），這個數對***都是質數，防止其他人進行猜測，其中3作為冪計算的底數，17作為求模的值。（這兩個概念不清楚的自己百度去）

交換的過程分為 3 part 。

第 1 part ：A 和 B 各自生成一個私鑰。

第 2 part ：A 和 B 進行指數運算，然后求模。

第 3 part ：A 和 B 對接收到的消息各自進行指數運算，然后求模，得到最終的公共的對稱密鑰。

這樣子，公共數 3、17、6、12 都是完全公開的，但是如果不擁有密鑰，想要靠猜的猜到 A 和 B 的公共密鑰是什么，還是需要很大的成本的，特別是我們把 3、17 這兩個公共數設置得非常非常大，然后 A 和 B 的私鑰也設置得非常非常大，這對于計算機來說短期內是不可破解的，甚至需要幾百萬年甚至更久，所以我們說這個算法是安全的。

那么，怎么保證 A 和 B 進行運算之后得到的數是一致的呢？

我們可以這樣看。

A 端：

接收到的 12 = 3^13 mod 17

所以 3 ^ 12 mod 17 = 3 ^ (13 * 12) mod 17

B 端:

接收到的 6 = 3^15 mod 17

所以 3 ^ 6 mod 17 = 3 ^ (12 * 13) mod 17

根據指數運算的規律，我們可以知道其實

 3 ^ 6 mod 17 = 3 ^ (12 * 13) mod 17 = 3 ^ (13 * 12) mod 17

好，無論這個最終計算到的數是什么，我們都可以保證 A 和 B 所擁有的密鑰是同一個值，然后后續所有的通訊都使用這個值進行加密運算然后傳輸就好了。

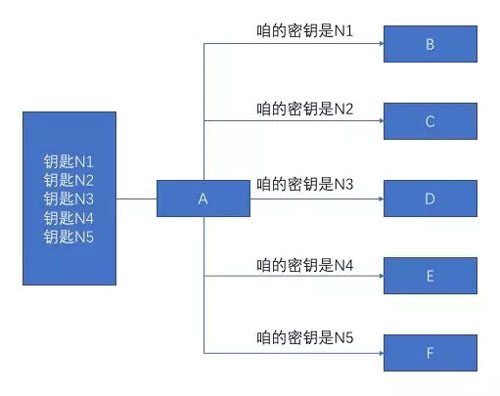
雖然這個方法很棒，但是你思考一下下面這個過程，如果 A 要跟 5 個人通信，那么 A 就要保存 5 個密鑰，久而久之，A會崩潰的。。。

如果不想這樣，那能怎么辦呢？關注后面的密碼學系列，可以解答這些問題。

【本文為51CTO專欄作者“大蕉”的原創稿件，轉載請通過作者微信公眾號“一名叫大蕉的程序員”獲取授權】

戳這里，看該作者更多好文