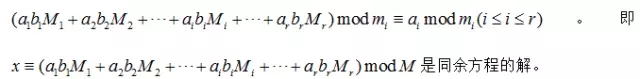愛恨交加的CRT——中國剩余定理
談到現代密碼學,其中數論的影響舉足輕重。計算機算法的實現、密碼算法的構造、軟硬件的優化,都離不開數論的理論支持。作為信息安全行業的工作者和學生,數論是我們無法繞開的高山,是心底無法撫平的憂傷。而中國剩余定理,算是***恨交織的那一部分吧。
遍尋信息安全的數學基礎,歐幾里得、歐拉、費爾馬、伽羅瓦都是西域來的高山,只有中國剩余定理,那是有古籍為證的咱中國特產。懷著自豪的心去聽,發現一樣聽不懂。感覺自己白進化了兩千年……
研究中國剩余定理以前,必須要了解其對信息安全行業的應用價值,以公鑰密碼為例。1976年,Diffie和Hellman提出的DH密鑰協商協議開創了基于數學難題的公鑰密碼新時代。公鑰密碼設計的基本思路是:尋找一個公認的數學難題,在難題的基礎上構建密碼算法。例如DH密鑰協商算法的有效性依賴于計算離散對數的難度,使得有限域中已知明文M計算密文C簡單,但已知C計算M困難。Alice與Bob為了安全通信,需要安全交換一個密鑰,于是他們倆分別選擇了自己的秘密a和b,g是雙方已知的大素數的原根,計算Ca=g^a,Cb=g^b,得到對方的Ca和Cb后,兩人分別計算Cab=Ca^b=Cb^a=g^ab,這樣,Alice與Bob偷偷完成了公共密鑰的協商,以后就可以加密通信啦。計算g^a,在數學家的手里就是一條公式,但真正操作起來,g和a可能是一個1024或2048位的二進制大數,我們現在的計算機CPU也不過能一次性操作64位的二進制——草稿紙都寫不下的數字怎么計算連乘?沒問題,中國剩余定理來幫你。
中國剩余定理原理
中國剩余定理(Chineseremaindertheorem,CRT),又稱為孫子剩余定理,最早見于《孫子算經》的下卷第28題“物不知數”:
有物不知其數,三三數之剩二,五五數之有三,七七數之有二,問物幾何?
大意是,這邊有一堆物品不知道數量,有人三個三個地數***剩了兩個,有人五個五個的數***剩了三個,有人七個七個的數***剩了兩個,請問這堆物品應該是多少個?
這道題很像民間傳說“韓信點兵”。秦朝末年,楚漢相爭。一次,韓信與楚王大將李鋒交戰。苦戰一場,楚軍不敵,敗退回營,漢軍也死傷四五百人,于是韓信整頓兵馬也返回大本營。當行至一山坡,忽有后軍來報,說有楚軍騎兵追來。只見遠方塵土飛揚,殺聲震天。漢軍本來已十分疲憊,這時隊伍大嘩。韓信兵馬到坡頂,見來敵不足五百騎,便急速點兵迎敵。他命令士兵3人一排,結果多出2名;接著命令士兵5人一排,結果多出3名;他又命令士兵7人一排,結果又多出2名。韓信馬上向將士們宣布:我軍有1073名勇士,敵人不足五百,我們居高臨下,以眾擊寡,一定能打敗敵人。于是漢軍士氣大振,一時間旌旗搖動,鼓聲喧天,漢軍步步進逼,楚軍亂作一團。交戰不久,楚軍大敗而逃。故事中韓信的點兵方法是中國剩余定理的一種實際應用了。
古人是如何描述剩余定理的呢?《孫子算經》后文給出了“物不知數”問題的剩余解法,“術曰:三三數之,剩二,置一百四十;五五數之,剩三,置六十三;七七數之,剩二,置三十。并之,得二百三十三,以二百一十減之,即得。凡三三數之,剩一,則置七十;五五數之,剩一,則置二十一;七七數之,剩一,則置十五。一百六以上,以一百五減之,即得。”“物不知數”為后來的“大衍求一術”的起源,被看作是中國數學史上最有創造性地成就之一,稱為中國剩余定理。
為方便讀者理解中國剩余定理,用現今的數論知識描述此定理如下[1]:
設m1,m2,…,mk是大于1的k(k≥2)個兩兩互素的正整數,b1,b2,…,bk∈Z,由k個一元一次同余方程聯立的方程組如下:
下面以我國古代數學家楊輝在1275年所寫的《續古摘奇算法》中的一道題目作為例子詳解中國剩余定理求解過程。
題目:二數余一,五數余二,七數余三,九數余四,問本數。
解:由題意有
中國剩余定理歷史發展演進
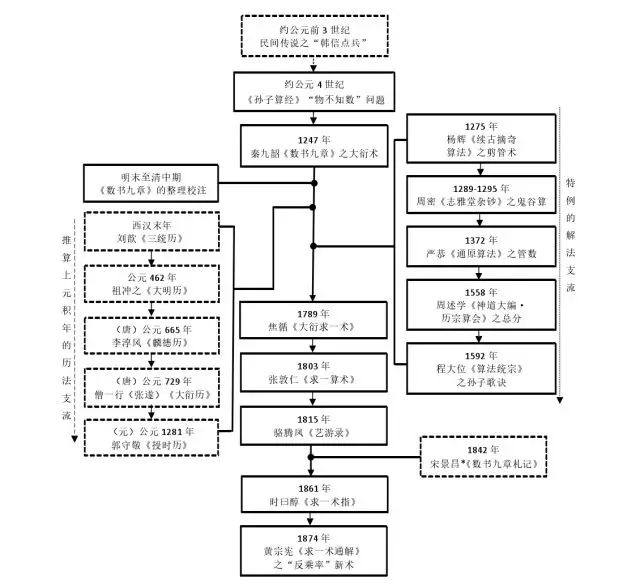
中國剩余定理歷史發展演進路線如下圖所示:
圖1中國剩余定理歷史發展演進路線簡圖[2]
中國剩余定理的應用
現代密碼學
在現代密碼學領域,RSA公鑰密碼體制至今仍被認可和采用,是公認的安全性良好的密碼體制,也是現階段比較常用的密碼體制。而基于中國剩余定理的單基數轉換法(SRC)和混合基數轉換法(MRC)可以快速實現RSA的解密,解密速度大約提高四倍左右,這在無論軟件還是硬件實現RSA密碼算法都是非常重要的[3]。中國剩余定理還可以應用在輕量級密碼設計、PKI認證系統、通信編碼等等,在信息安全領域中占有非常重要的地位。
多項式
結語
在一次同余式組問題上,中國剩余定理的研究在古代遠遠領先于世界,可以說明中國人的數學能力是及其出眾的。古人對數學的貢獻是我們的寶貴財富,中國剩余定理在密碼學上的應用只是其價值的部分體現,愿研究者們可以充分利用這些財富創造更多更大的榮耀。
參考文獻
[1]谷利澤、楊義先.現代密碼學教程[M].北京郵電大學出版社出版.2009:53
[2]鄧真崢.中國剩余定理的中外歷史發展比較[D].四川師范大學,2017.
[3]賀毅朝,劉建芹,陳維海.中國剩余定理在RSA解密中的應用[J].河北省科學院學報,2003,20(3):138-143.
【本文為51CTO專欄作者“中國保密協會科學技術分會”原創稿件,轉載請聯系原作者】