沒有完美的數據插補法,只有最適合的
大數據文摘出品
編譯:張秋玥、胡笳、夏雅薇
數據缺失是數據科學家在處理數據時經常遇到的問題,本文作者基于不同的情境提供了相應的數據插補解決辦法。沒有完美的數據插補法,但總有一款更適合當下情況。
我在數據清理與探索性分析中遇到的最常見問題之一就是處理缺失數據。首先我們需要明白的是,沒有任何方法能夠完美解決這個問題。不同問題有不同的數據插補方法——時間序列分析,機器學習,回歸模型等等,很難提供通用解決方案。在這篇文章中,我將試著總結最常用的方法,并尋找一個結構化的解決方法。
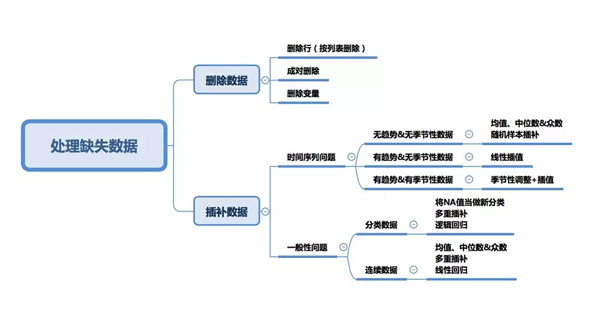
一、插補數據vs刪除數據
在討論數據插補方法之前,我們必須了解數據丟失的原因。
- 隨機丟失(MAR,Missing at Random):隨機丟失意味著數據丟失的概率與丟失的數據本身無關,而僅與部分已觀測到的數據有關。
- 完全隨機丟失(MCAR,Missing Completely at Random):數據丟失的概率與其假設值以及其他變量值都完全無關。
- 非隨機丟失(MNAR,Missing not at Random):有兩種可能的情況。缺失值取決于其假設值(例如,高收入人群通常不希望在調查中透露他們的收入);或者,缺失值取決于其他變量值(假設女性通常不想透露她們的年齡,則這里年齡變量缺失值受性別變量的影響)。
在前兩種情況下可以根據其出現情況刪除缺失值的數據,而在第三種情況下,刪除包含缺失值的數據可能會導致模型出現偏差。因此我們需要對刪除數據非常謹慎。請注意,插補數據并不一定能提供更好的結果。
二、刪除
1. 列表刪除
按列表刪除(完整案例分析)會刪除一行觀測值,只要其包含至少一個缺失數據。你可能只需要直接刪除這些觀測值,分析就會很好做,尤其是當缺失數據只占總數據很小一部分的時候。然而在大多數情況下,這種刪除方法并不好用。因為完全隨機缺失(MCAR)的假設通常很難被滿足。因此本刪除方法會造成有偏差的參數與估計。
- newdata <- na.omit(mydata)
- # In python
- mydata.dropna(inplace=True)
2. 成對刪除
在重要變量存在的情況下,成對刪除只會刪除相對不重要的變量行。這樣可以盡可能保證充足的數據。該方法的優勢在于它能夠幫助增強分析效果,但是它也有許多不足。它假設缺失數據服從完全隨機丟失(MCAR)。如果你使用此方法,最終模型的不同部分就會得到不同數量的觀測值,從而使得模型解釋非常困難。
觀測行3與4將被用于計算ageNa與DV1的協方差;觀測行2、3與4將被用于計算DV1與DV2的協方差。
- #Pairwise Deletion
- ncovMatrix <- cov(mydata, use="pairwise.complete.obs")
- #Listwise Deletion
- ncovMatrix <- cov(mydata, use="complete.obs")
3. 刪除變量
在我看來,保留數據總是比拋棄數據更好。有時,如果超過60%的觀測數據缺失,直接刪除該變量也可以,但前提是該變量無關緊要。話雖如此,插補數據總是比直接丟棄變量好一些。
- df <- subset(mydata, select = -c(x,z) )
- df <- mydata[ -c(1,3:4) ]
- In python
- del mydata.column_name
- mydata.drop('column_name', axis=1, inplace=True)
- Time-Series Specific Methods
三、時間序列分析專屬方法
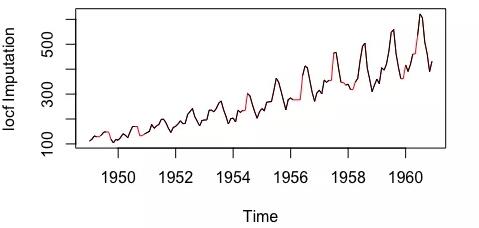
前推法(LOCF,Last Observation Carried Forward,將每個缺失值替換為缺失之前的最后一次觀測值)與后推法(NOCB,Next Observation Carried Backward,與LOCF方向相反——使用缺失值后面的觀測值進行填補)
這是分析可能缺少后續觀測值的縱向重復測量數據的常用方法。縱向數據在不同時間點跟蹤同一樣本。當數據具有明顯的趨勢時,這兩種方法都可能在分析中引入偏差,表現不佳。
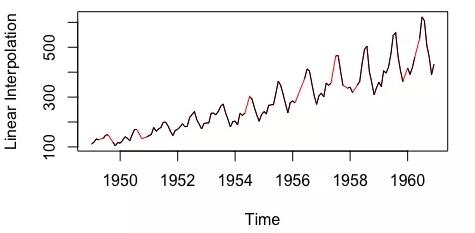
線性插值。此方法適用于具有某些趨勢但并非季節性數據的時間序列。
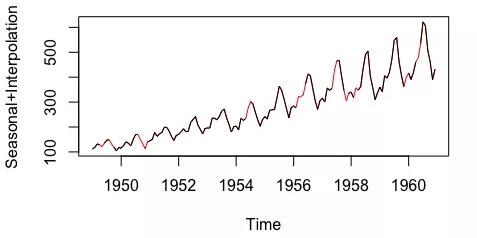
季節性調整+線性插值。此方法適用于具有趨勢與季節性的數據。
季節性+插值法
線性插值法
LOCF插補法
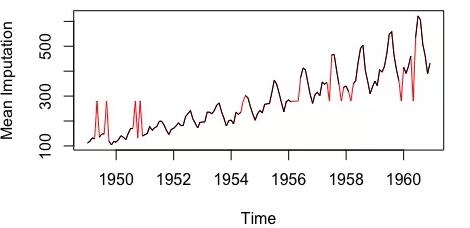
均值插補法
注:以上數據來自imputeTS庫的tsAirgap;插補數據被標紅。
- library(imputeTS)
- na.random(mydata) # Random Imputation
- na.locf(mydata, option = "locf") # Last Obs. Carried Forward
- na.locf(mydata, option = "nocb") # Next Obs. Carried Backward
- na.interpolation(mydata) # Linear Interpolation
- na.seadec(mydata, algorithm = "interpolation") # Seasonal Adjustment then Linear Interpolation
四、均值,中位數與眾數
計算整體均值、中位數或眾數是一種非常基本的插補方法,它是唯一沒有利用時間序列特征或變量關系的測試函數。該方法計算起來非常快速,但它也有明顯的缺點。其中一個缺點就是,均值插補會減少數據的變化差異(方差)。
- library(imputeTS)
- na.mean(mydata, option = "mean") # Mean Imputation
- na.mean(mydata, option = "median") # Median Imputation
- na.mean(mydata, option = "mode") # Mode Imputation
- In Python
- from sklearn.preprocessing import Imputer
- values = mydata.values
- imputer = Imputer(missing_values=’NaN’, strategy=’mean’)
- transformed_values = imputer.fit_transform(values)
- # strategy can be changed to "median" and “most_frequent”
五、線性回歸
首先,使用相關系數矩陣能夠選出一些缺失數據變量的預測變量。從中選擇最靠譜的預測變量,并將其用于回歸方程中的自變量。缺失數據的變量則被用于因變量。自變量數據完整的那些觀測行被用于生成回歸方程;其后,該方程則被用于預測缺失的數據點。在迭代過程中,我們插入缺失數據變量的值,再使用所有數據行來預測因變量。重復這些步驟,直到上一步與這一步的預測值幾乎沒有什么差別,也即收斂。
該方法“理論上”提供了缺失數據的良好估計。然而,它有幾個缺點可能比優點還值得關注。首先,因為替換值是根據其他變量預測的,他們傾向于“過好”地組合在一起,因此標準差會被縮小。我們還必須假設回歸用到的變量之間存在線性關系——而實際上他們之間可能并不存在這樣的關系。
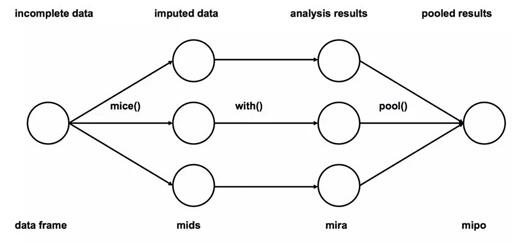
六、多重插補
- 插補:將不完整數據集缺失的觀測行估算填充m次(圖中m=3)。請注意,填充值是從某種分布中提取的。模擬隨機抽取并不包含模型參數的不確定性。更好的方法是采用馬爾科夫鏈蒙特卡洛模擬(MCMC,Markov Chain Monte Carlo Simulation)。這一步驟將生成m個完整的數據集。
- 分析:分別對(m個)每一個完整數據集進行分析。
- 合并:將m個分析結果整合為最終結果。
來源:http://www.stefvanbuuren.nl/publications/mice%20in%20r%20-%20draft.pdf
- # We will be using mice library in r
- library(mice)
- # Deterministic regression imputation via mice
- imp <- mice(mydata, method = "norm.predict", m = 1)
- # Store data
- data_imp <- complete(imp)
- # Multiple Imputation
- imp <- mice(mydata, m = 5)
- #build predictive model
- fit <- with(data = imp, lm(y ~ x + z))
- #combine results of all 5 models
- combine <- pool(fit)
這是迄今為止最優選的插補方法,因為它非常易于使用,并且在插補模型正確的情況下它不會引入偏差。
七、分類變量插補
- 眾數插補法算是一個法子,但它肯定會引入偏差。
- 缺失值可以被視為一個單獨的分類類別。我們可以為它們創建一個新類別并使用它們。這是最簡單的方法了。
- 預測模型:這里我們創建一個預測模型來估算用來替代缺失數據位置的值。這種情況下,我們將數據集分為兩組:一組剔除缺少數據的變量(訓練組),而另一組則包括缺失變量(測試組)。我們可以用邏輯回歸和ANOVA等方法來進行預測。
- 多重插補法。
八、KNN(K近鄰)
能夠用于數據插補的機器學習方法有很多,比如XGBoost與Random Forest,但在這里我們討論KNN方法,因為它被廣泛應用。在本方法中,我們根據某種距離度量選擇出k個“鄰居”,他們的均值就被用于插補缺失數據。這個方法要求我們選擇k的值(最近鄰居的數量),以及距離度量。KNN既可以預測離散屬性(k近鄰中最常見的值)也可以預測連續屬性(k近鄰的均值)。
根據數據類型的不同,距離度量也不盡相同:
- 連續數據:最常用的距離度量有歐氏距離,曼哈頓距離以及余弦距離。
- 分類數據:漢明(Hamming)距離在這種情況比較常用。對于所有分類屬性的取值,如果兩個數據點的值不同,則距離加一。漢明距離實際上與屬性間不同取值的數量一致。
KNN算法最吸引人的特點之一在于,它易于理解也易于實現。其非參數的特性在某些數據非常“不尋常”的情況下非常有優勢。
KNN算法的一個明顯缺點是,在分析大型數據集時會變得非常耗時,因為它會在整個數據集中搜索相似數據點。此外,在高維數據集中,最近與最遠鄰居之間的差別非常小,因此KNN的準確性會降低。
- library(DMwR)
- knnOutput <- knnImputation(mydata)
- In python
- from fancyimpute import KNN
- # Use 5 nearest rows which have a feature to fill in each row's missing features
- knnOutput = KNN(k=5).complete(mydata)
在上述方法中,多重插補與KNN最為廣泛使用,而由于前者更為簡單,因此其通常更受青睞。
相關報道:https://towardsdatascience.com/how-to-handle-missing-data-8646b18db0d4
【本文是51CTO專欄機構大數據文摘的原創文章,微信公眾號“大數據文摘( id: BigDataDigest)”】