通常在拿到一份數據進行相關的模型訓練之前，我們需要進行數據清洗以便得到干凈的數據。進一步需要找到與問題有關的特征信息，并把這些特征轉換成特征矩陣的數值，這也就是機器學習實踐中的重要步驟之一，特征工程。本系列文章將從數據特征的分布分析、對比分析、統計分析、貢獻度分析(帕累托分析)、和特征的相關性分析來識別數據集整體上的一些重要性質。

本文目錄

1. 特征分布分析
2. 特征對比分析
3. 特征統計分析
4. 特征貢獻度分析
5. 特征相關性分析

01、分布分析

理論介紹：分布分析是用來解釋數據的分布類型和分布特征，顯示其分布情況。所以可以對一開始拿到數據可以首先進行初步的分布分析。分布分析主要分成兩種：

• ①對定量的數據進行分布分析
• ②對定性的數據進行分布分析。

對定量數據的分布分析按照如下步驟進行：

1. 求極差
2. 決定組距與組數
3. 決定分點
4. 繪制頻率分布圖

對定性的數據分布分析：

• 根據變量的分類類型來確定分組，然后使用圖形對信息進行顯示。

Python分析結果:

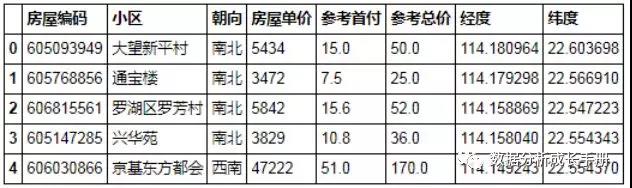
• 比如現在你爬取到某地區的二手房信息數據，針對這一批數據的房價你要做一次定量分布分析，以及對不同房子的朝向做一個定性的分布分析，以便初步的了解房子的一些特征分布。

參考房價定量分析

1.首先利用pandas讀取數據并取前五條數據得到如下信息。

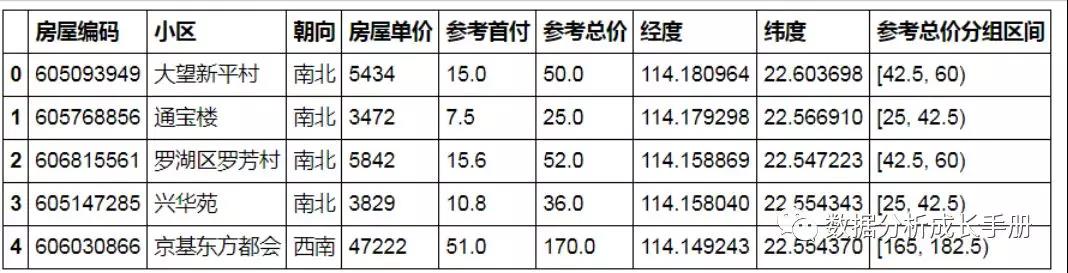
2.求參考總價的分組區間并在原始數據中添加一個新的字段“參考總價分組區間”。

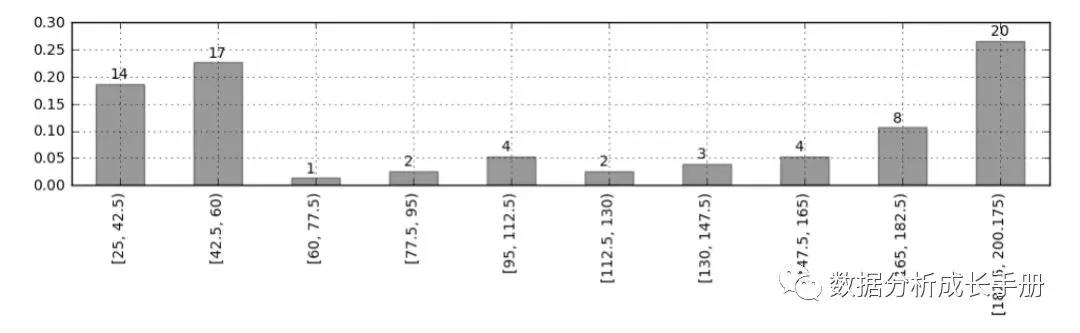
3.計算每段參考總價的區間的頻數、頻率并繪制直方圖。

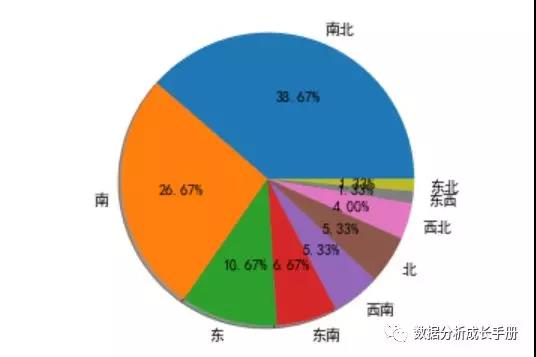
房屋朝向定性分析

對不同房屋朝向占比可繪制一個餅圖。

 

 

02、對比分析 

理論介紹：對比分析是指把兩個相互聯系的指標進行比較，從數量上展示和說明研究對象規模的大小、水平的高低、速度的快慢，以及各種關系是否協調。特別適用于指標間的橫縱向比較、時間序列的比較分析。在對比分析中，選擇合適的對比標準是十分關鍵的步驟，選擇合適，才能做出客觀的評價，選擇不合適，評價可能得出錯誤的結論。

對比分析主要分為以下兩種形式：

絕對數比較

利用這組指標絕對數進行對比，從而尋找差異的一種方法。

相對數比較

它是由兩個有聯系的指標對比計算的，用以反映客觀現象之間數量聯系程度的綜合指標，其數值表現為相對數。由于研究目的和對比基礎不用，相對數可以分為以下幾種：結構相對數、比例相對數、動態相對數和空間相對數

Python分析結果：

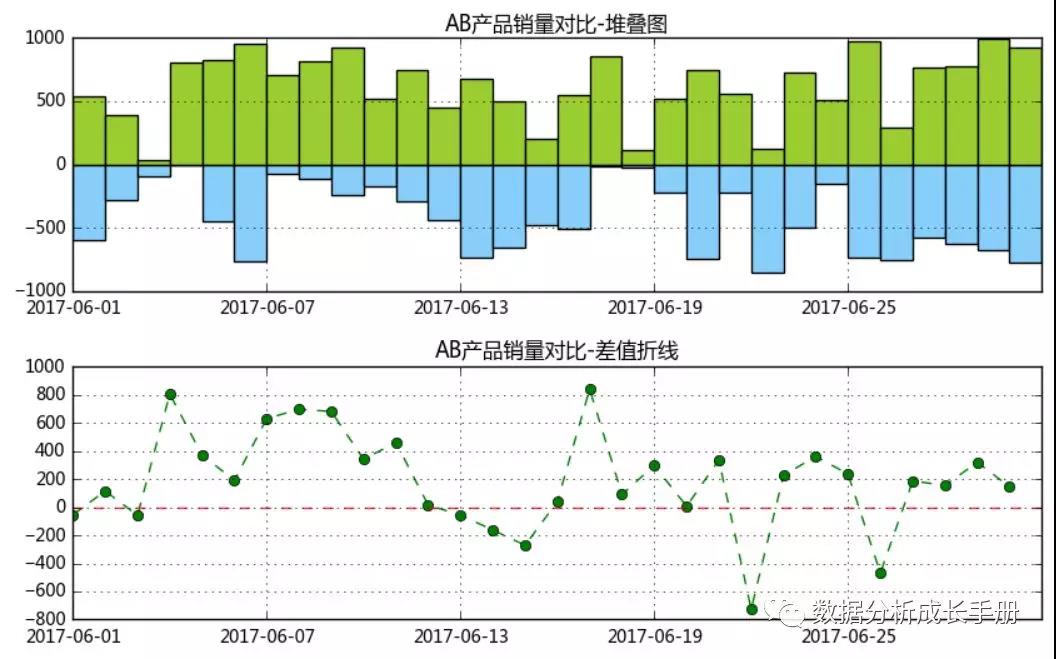
絕對數比較案例：比如現在有某公司的A、B產品某月銷量數據，這里我們可以對A、B產品的銷量做絕對數對比。

相對數比較案例：

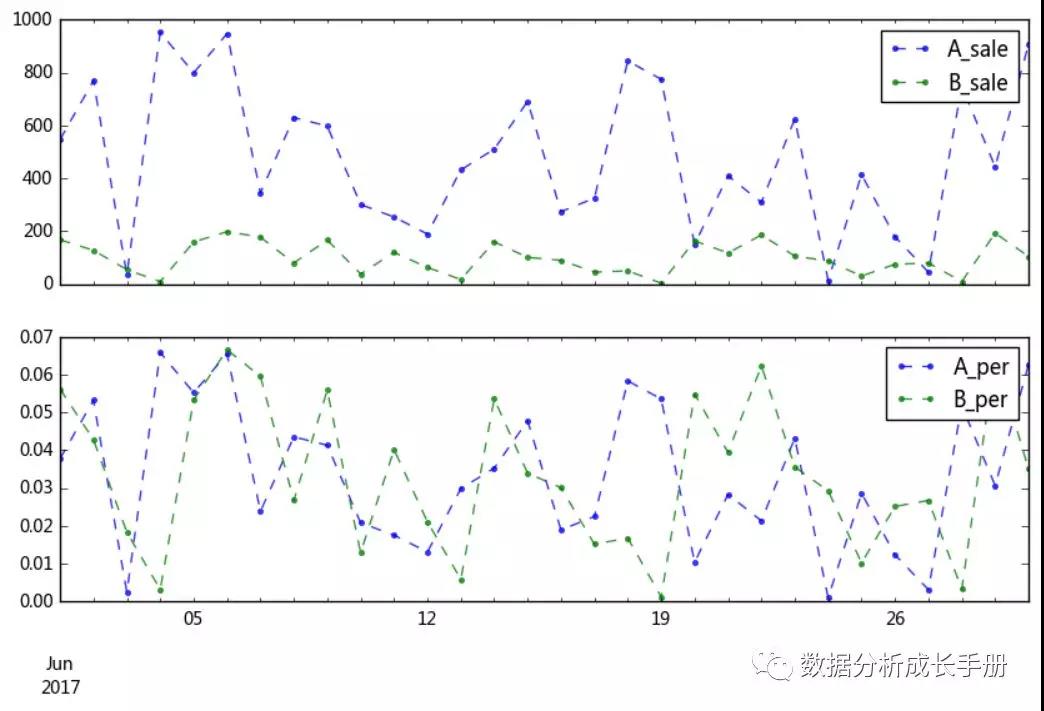
結構相對數：在分組基礎上，各組總量指標與總體的總量指標對比，計算出各組數量在總量中所占比重。例如，30天內A、B產品的日銷售額，由于 A、B產品銷售額量級不同，計算出A、B產品每日銷售額占該月各自總銷售額對比。

比例相對數：比例相對數 = 總體中某一部分數值 / 總體中另一部分數值 。如 “基本建設投資額中工業、農業、教育投資的比例”、“男女比例”

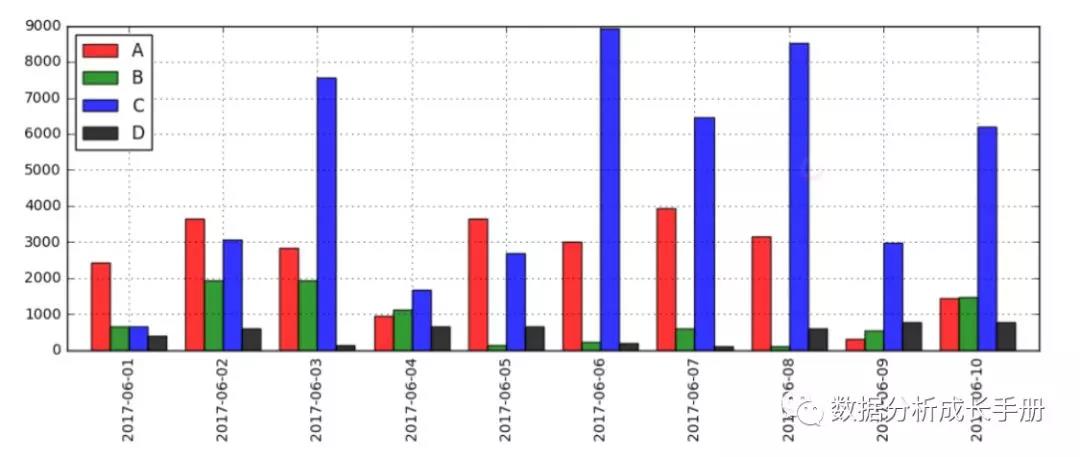
空間相對數(橫向)：比如說同樣的2017年北京和深圳膜拜單車使用量，空間是比較抽象的更多的是在時間相同的情況下，不同的元素的比較 。

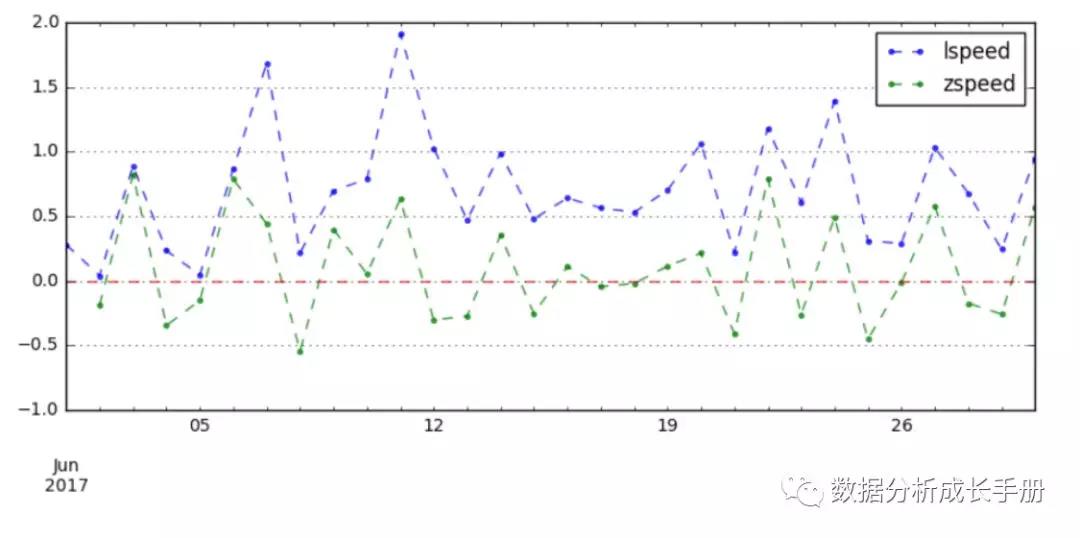
動態相對數(縱向)：將同一現象在不同時期的指標數值對比，用以說明發展方向和變化的速度，如發展速度、增長速度等。例如求A產品的某月的定基增長速度額環比增長速度 

03、統計分析

1. 理論介紹：對一組數據用統計指標定量的分析數據，一般從集中趨勢和離中趨勢兩個方面來衡量數據。
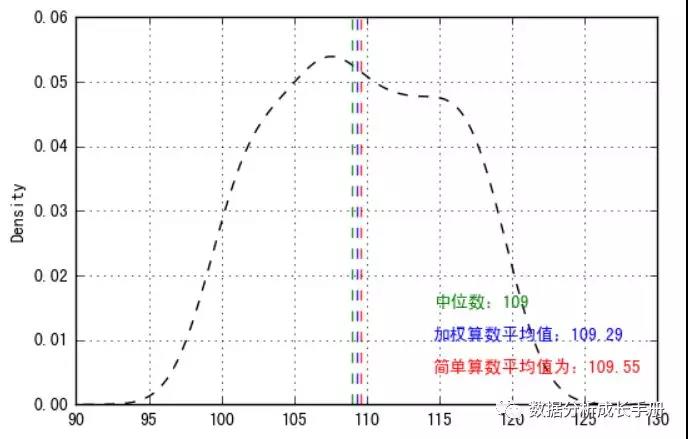
2. 數據的集中趨勢：指一組數據向某一中心靠攏的傾向，核心在于尋找數據的代表值或中心值 ，所以需要找到數據的統計平均數來衡量。統計平均數可分為，①算術平均數、加權算術平均數②位置平均數。
3. 數據的離中趨勢：指一組數據中各數據以不同程度的距離偏離中心的趨勢，可用極差與分位差、方差與標準差、離散系數 等衡量。

Python結果分析：

對某一組數據分析其集中趨勢結果：

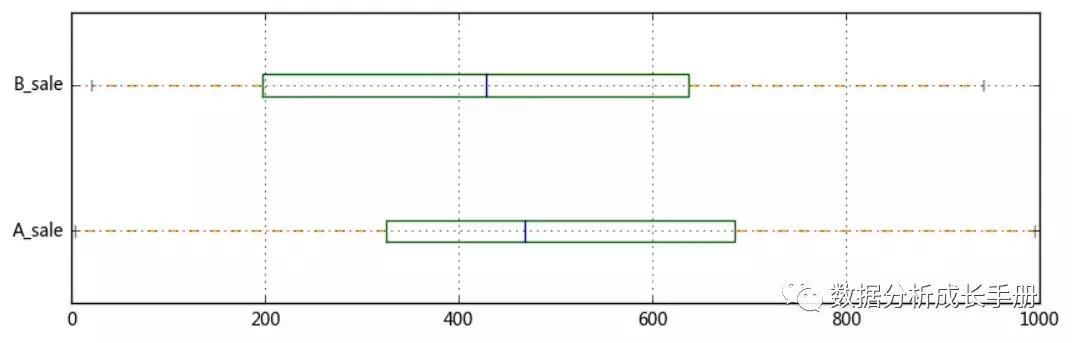
對某一組數據分析其離中趨勢結果：

• 你要比較A、B數據的分散程度，可求得其分位差和其他指標。你可以繪制箱型圖對比。 

04、帕累托分析

理論介紹：帕累托分析又叫貢獻度分析，原理是20/80定律，即80%的利潤常常來自于20%的產品。一般來說投入產出，努力和報酬之間并不是絕對的線性關系，總有一些關鍵因素起著至關重要的作用，而帕累托分析就是找到影響事務的關鍵因素，分清主次。

Python代碼結果分析：

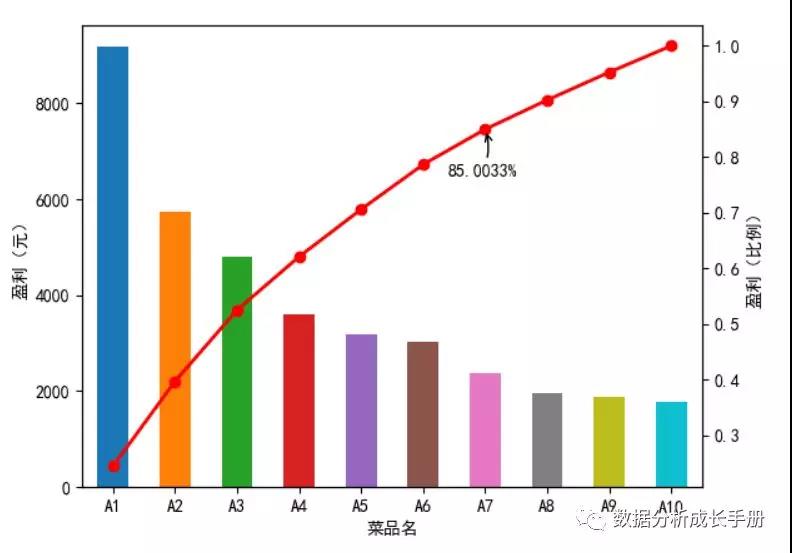
例如現在你有一份餐廳的不同菜品的盈利數據，你想找到哪些菜對該菜廳的盈利貢獻***。可按照如下步驟來實現貢獻度分析：

• 對不同菜品按盈利額排序
• 計算累積占比
• 找到累積占比85%的菜品，并找到其對應的索引位置。
• 繪制盈利圖并標記核心位置。 

05、相關性分析

理論介紹：相關性分析是研究兩個或兩個以上處于同等地位的隨機變量間的相關關系的統計分析方法。例如，人的身高和體重之間;空氣中的相對濕度與降雨量之間的相關關系都是相關分析研究的問題。相關分析與回歸分析之間的區別：回歸分析側重于研究隨機變量間的依賴關系，以便用一個變量去預測另一個變量;相關分析側重于發現隨機變量間的種種相關特性。可用相關系數r來衡量兩個特征之間的相關性。

相關系數r的解讀：

• 正相關：如果x,y變化的方向一致，如登陸次數和商機用戶的關系，r>0;一般地， |r|>0.95 存在顯著性相關|r|≥0.8 高度相關;0.5≤|r|<0.8 中度相關0.3≤|r|<0.5 低度相關;|r|<0.3 關系極弱，認為不相關。
• 負相關：如果x,y變化的方向相反，如吸煙與肺功能的關系，r<0
• 無線性相關：r=0。

關于相關系數的計算有三種：

• ①Pearson相關系數
• ②Spearman秩相關系數
• ③Kendall相關系數。

注意點：皮爾遜相關系數的計算是數據分布為正太分布，所以計算之前要先進行正態性檢驗。對于不服從正太分布變量的關聯性可用斯皮爾曼相關系數來計算，也叫等級相關系數。

Python結果分析：

首先對數據進行正太性檢驗，利用scipy里面集成好的K-S檢驗方法。

2. 利用pandas里面集成好的相關系數計算方法。

總結：本文對數據特征的一些常用分析方法進行了系統介紹，并利用Python里面的科學計算庫Numpy、Pandas、Scipy、Matplotlib實現了每一種分析方法的分析結果，并且將結果圖形化顯示出來。