十分鐘了解UV統計算法HyperLogLog
前段時間產品提了個需求,需要統計APP的各個場景下的UV,如何實現?
1、方案
考慮到上述問題的擴展性,除了統計APP每日的獨立用戶登錄數,還需要統計打開每個頁面的獨立用戶數。
方案一:用Set統計
首先我們想到肯定是通過類似 redis 的 Set,將每個openid添加到對應需要統計的 Set 中,每一種類型用一個 Set,那計算一下,如果存儲1億個key,每個key的大小32個字符,大約存儲空間是:
100000000 * 32 * 8 = 23G以上只是計算一種類型,如果有100種類型,那么這個存儲空間線性增長。當然,對于存儲多個類型可以通過稀疏矩陣優化,但是實際的存儲空間還是比較大。
方案二:用bitmap統計
方案一最大的問題是存儲 Set,但是我們需要的信息是存在或者不存在,那么這里其實用 bitmap 位運算0或1就可以解決當前問題,那么存儲1億個key,每個key需要1個bit位,大約存儲空間是:
100000000 * 1 / 8 = 12M如果有100種類型,那么存儲空間是1.2G左右,這種方法可以解決內存過大的問題,但是無法擴展。
方案三:概率算法統計
在解決大數據量的情況下,很多實際場景不需要太精確的數據,為了節省內存同時滿足大數據的統計需求,衍生了很多概率算法,如:
- Linear Counting:定義一個hash函數,function hash(x): -> [0,1,2,…,m-1],假設該hash函數的hash結果服從均勻分布,接著定義一個長度為m的bit數組,開始每一位上都初始化為0,然后對可重復集合里的每個元素進行hash得到k,如果bitmap[k]為0則置1,最后統計bitmap數組里為0的位數;
- LogLog Counting:LogLog Counting優于Linear Counting,也是利用哈希函數將輸入元素映射到一個固定大小的位數組中,估算連續數組的位數,時間復雜度為O(1);
- HyperLogLog Counting:是基于LogLog Counting的改進方案,能實現更小的誤差,本文重點就介紹HyperLogLog Counting算法;
2、HyperLogLog Counting原理
用一句話概括:我們能找到連續出現的概率與次數的關系,能就能將其轉換為數學公式。比如我們有數組:
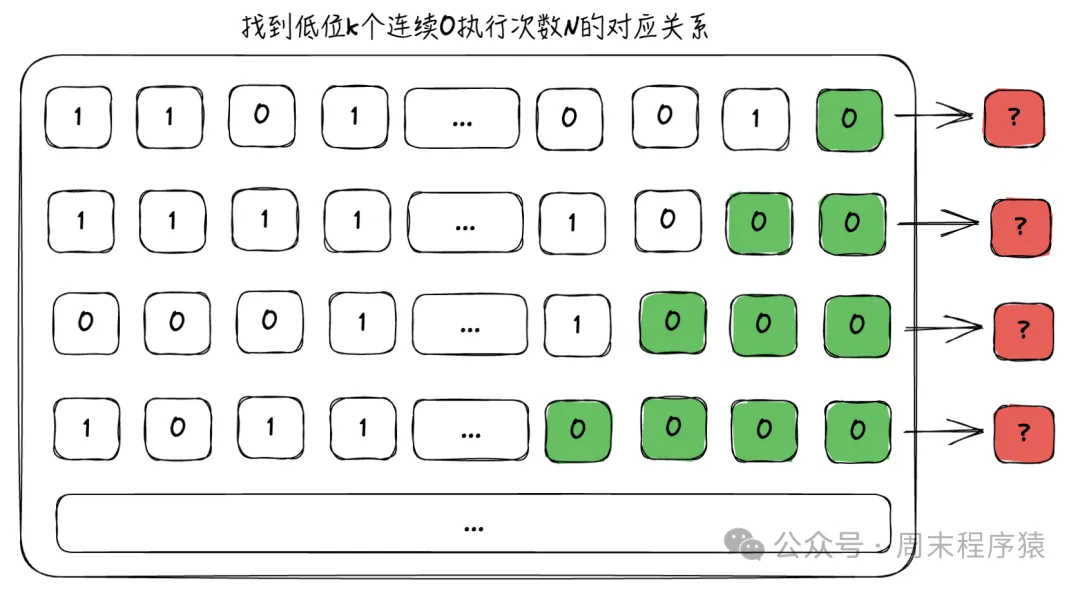 數組
數組
通過上圖我們只需要末尾連續0的個數,并統計出執行多少次隨機即可,我們用如下代碼實驗:
import random
import math
class LogLogV1:
def __init__(self, maxbit: int, tries: int = 10):
"""
maxbit: int, 連續0的個數
tries: int, 重復次數
"""
self.maxbit = maxbit
self.tries = tries
self.option = [0, 1]
def _run_one_round(self):
rounds = 0
while True:
num = 0
while True:
result = random.choice(self.option)
if result == 1:
break
num += 1
rounds += 1
if num >= self.maxbit:
break
return rounds
def get_rounds(self):
all_rounds = 0
for i in range(self.tries):
all_rounds += self._run_one_round()
return all_rounds / self.tries
if __name__ == '__main__':
for i in range(10, 20):
be = LogLogV1(i)
rounds = be.get_rounds()
print(f"{i} rounds: {rounds}, log2: ", math.log(rounds, 2))以上代碼的含義是,獲得連續 maxbit = 0,需要執行的次數是多少,這里通過 tries 重復次數來求平均值,最后輸出:
10 rounds: 1023.7, log2: 9.99957727351139
11 rounds: 2041.0, log2: 10.995060467032719
12 rounds: 2649.1, log2: 11.371286589215627
13 rounds: 16484.6, log2: 14.008831259883943
14 rounds: 20324.1, log2: 14.31090384726008
15 rounds: 25673.7, log2: 14.648003606393374
16 rounds: 70248.2, log2: 16.10017363855784
17 rounds: 152139.1, log2: 17.2150314501608
18 rounds: 267469.5, log2: 18.029014862371255
19 rounds: 627246.3, log2: 19.258672529927942可以看到 2^maxbit ≈ rounds,其中誤差比較小。
3、HyperLogLog Counting分桶
為什么要分桶?假設上述的tries值比較小,那么會存在估計不準的情況,比如 2^maxbit ~ 2^(maxbit+1) 之間直接按照公式計算,誤差會比較大,所以通過求多個值得平均值來解決問題,這樣估算的值就比較平滑。
那么redis的HyperLogLog Counting是如何分桶的?代碼:https://github.com/redis/redis/blob/unstable/src/hyperloglog.c
- 2^14個桶,每個桶6bit,總共12KB;
- 每個輸入通過hash算法得出64bit哈希值hashkey;
- hashkey的低14位,用來選擇桶號(0-2^14-1號)Mi;
- hashkey的高50位,用來找K(也就是第一次出現1的位置,或者說0后綴的長度),把K存入Mi;
網上有個模擬演示地址:http://content.research.neustar.biz/blog/hll.html,有興趣可以看看詳細的執行過程。
4、擴展
(1)HyperLogLog能滿足產品的需求,但是擴展到其他問題:如何實現長周期存儲(一年的存儲周期UV統計);(2)如何實現分布式,本身HyperLogLog是單機算法,如何實現非集中式場景;
參考
https://www.cnblogs.com/wmyskxz/p/12396393.html




































