大數據算法及應用場景首篇:統計與分布
算法是大數據的最核心價值部分。大數據的挖掘是從海量、不完整、噪聲、模糊、隨機、碎片數據中發現其中隱藏的價值,以及潛在的有用信息和知識的過程。什么情況用什么算法呢?今天給大家做個大數據算法入門。
一、統計分布
統計分布(frequency distribution)亦稱“次數(頻數)分布(分配)”。在統計分組的基礎上,將總體中的所有單位按組歸類整理,形成總體單位在各組間的分布。分布在各組中的單位數叫做次數或頻數。各組次數與總次數(全部總體單位數)之比,稱為比率或頻率。將各組別與次數依次編排而成的數列就叫做統計分布數列,簡稱分布數列或分配數列。它可以反映總體中所有單位在各組間的分布狀態和分布特征,研究這種分布特征是統計分析的一項重要內容。如上的BLABLA的一堆,具體來看看到底能干什么吧。
1)平均值
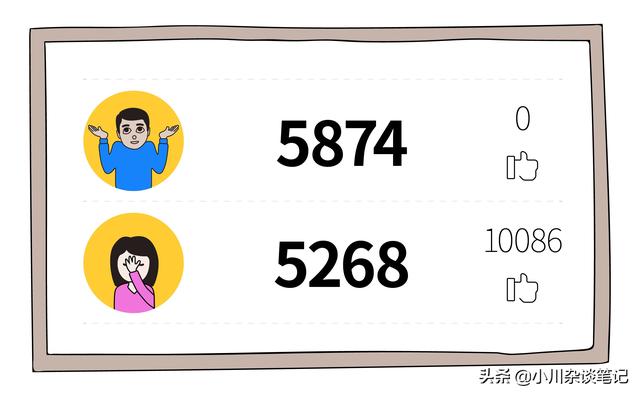
舉個栗子!中國男人背上“油膩”一詞好幾年了,根據《2017中國人運動報告》數據顯示,至少在步行量上,男生要高于女生:男生平均每天走5874步,女生日均步數達到5268步。注重運動加上更新一下觀念,中國男人或許能保持一下少年感。
2)同比和環比
同比一般情況下是今年第n月與去年第n月比。
環比,表示連續2個單位周期(比如連續兩月)內的量的變化比。

3)高斯分布
正態分布(Normal distribution),也稱“常態分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度導出了它。P.S.拉普拉斯和高斯研究了它的性質。是一個在數學、物理及工程等領域都非常重要的概率分布,在統計學的許多方面有著重大的影響力。
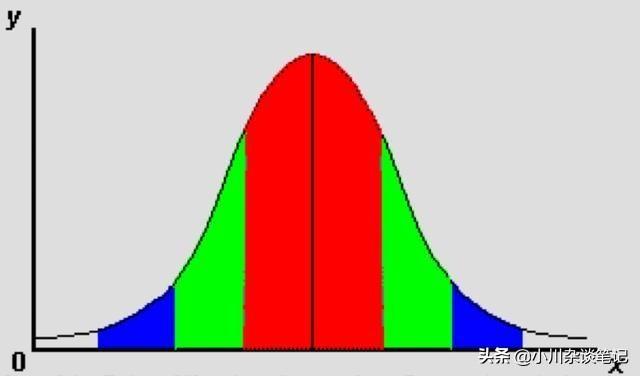
高斯分布怎么用?舉個栗子:這張圖大家都見過吧。收集盡量多的用戶的開機時間,然后,查看時間的分布如何。
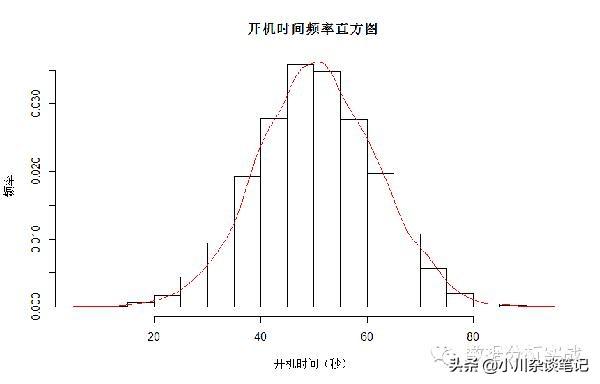
4)柏松分布
Poisson分布,是一種統計與概率學里常見到的離散概率分布,由法國數學家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年時發表。
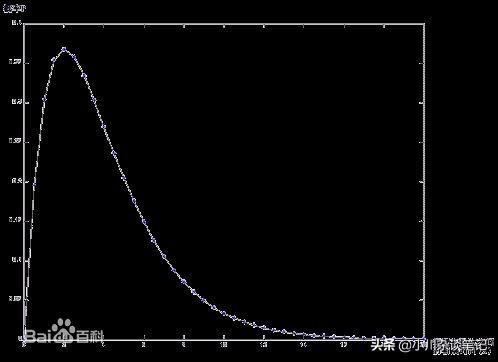
小小柏松分布在大數據領域可以解決大大的問題!干貨來了!
栗子1:玩電商和倉儲的,進來看看。已知某家小雜貨店,平均每周售出2個水果罐頭。請問該店水果罐頭的***庫存量是多少?
假定不存在季節因素,可以近似認為,這個問題滿足以下三個條件:
- a.顧客購買水果罐頭是小概率事件。
- b.購買水果罐頭的顧客是獨立的,不會互相影響。
- c.顧客購買水果罐頭的概率是穩定的。
在統計學上,只要某類事件滿足上面三個條件,它就服從"泊松分布"。
根據公式,計算得到每周銷量的分布:從上表可見,如果存貨4個罐頭,95%的概率不會缺貨(平均每19周發生一次);如果存貨5個罐頭,98%的概率不會缺貨(平均59周發生一次)。
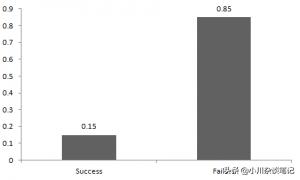
5)伯努利分布
伯努利分布(英語:Bernoulli distribution,又名兩點分布或者0-1分布,是一個離散型概率分布,為紀念瑞士科學家雅各布·伯努利而命名。)。通俗講,一件事情,只有兩種可能的結果。伯努利分布描述了其中一種結果的概率為a,另一種結果的概率為100%-a。再通俗的講,生一次孩子,生男孩子概率為p,生女孩紙概率1-p,這個就是伯努利分布。