一文讀懂自動編碼器的前世今生
變分自動編碼器(VAE)可以說是最實用的自動編碼器,但是在討論VAE之前,還必須了解一下用于數(shù)據(jù)壓縮或去噪的傳統(tǒng)自動編碼器。
變分自動編碼器的厲害之處
假設(shè)你正在開發(fā)一款開放性世界端游,且游戲里的景觀設(shè)定相當(dāng)復(fù)雜。
你聘用了一個圖形設(shè)計團(tuán)隊來制作一些植物和樹木以裝飾游戲世界,但是將這些裝飾植物放進(jìn)游戲中之后,你發(fā)現(xiàn)它們看起來很不自然,因為同種植物的外觀看起來一模一樣,這時你該怎么辦呢?
首先,你可能會建議使用一些參數(shù)化來嘗試隨機地改變圖像,但是多少改變才足夠呢?又需要多大的改變呢?還有一個重要的問題:實現(xiàn)這種改變的計算強度如何?
這是使用變分自動編碼器的理想情況。我們可以訓(xùn)練一個神經(jīng)網(wǎng)絡(luò),使其學(xué)習(xí)植物的潛在特征,每當(dāng)我們將一個植物放入游戲世界中,就可以從“已學(xué)習(xí)”的特征中隨機抽取一個樣本,生成獨特的植物。事實上,很多開放性世界游戲正在通過這種方法構(gòu)建他們的游戲世界設(shè)定。
再看一個更圖形化的例子。假設(shè)我們是一個建筑師,想要為任意形狀的建筑生成平面圖。可以讓一個自動編碼器網(wǎng)絡(luò)基于任意建筑形狀來學(xué)習(xí)數(shù)據(jù)生成分布,它將從數(shù)據(jù)生成分布中提取樣本來生成一個平面圖。詳見下方的動畫。
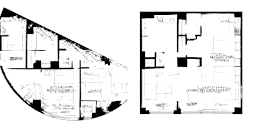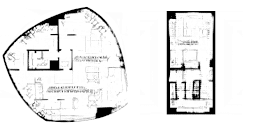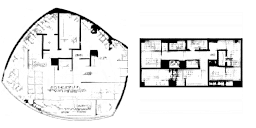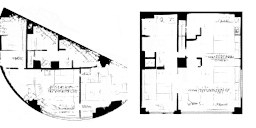
對于設(shè)計師來說,這些技術(shù)的潛力無疑是最突出的。
再假設(shè)我們?yōu)橐粋€時裝公司工作,需要設(shè)計一種新的服裝風(fēng)格,可以基于“時尚”的服裝來訓(xùn)練自動編碼器,使其學(xué)習(xí)時裝的數(shù)據(jù)生成分布。隨后,從這個低維潛在分布中提取樣本,并以此來創(chuàng)造新的風(fēng)格。
在該節(jié)中我們將研究fashion MNIST數(shù)據(jù)集。
自動編碼器
傳統(tǒng)自動編碼器
自動編碼器其實就是非常簡單的神經(jīng)結(jié)構(gòu)。它們大體上是一種壓縮形式,類似于使用MP3壓縮音頻文件或使用jpeg壓縮圖像文件。
自動編碼器與主成分分析(PCA)密切相關(guān)。事實上,如果自動編碼器使用的激活函數(shù)在每一層中都是線性的,那么瓶頸處存在的潛在變量(網(wǎng)絡(luò)中最小的層,即代碼)將直接對應(yīng)(PCA/主成分分析)的主要組件。通常,自動編碼器中使用的激活函數(shù)是非線性的,典型的激活函數(shù)是ReLU(整流線性函數(shù))和sigmoid/S函數(shù)。
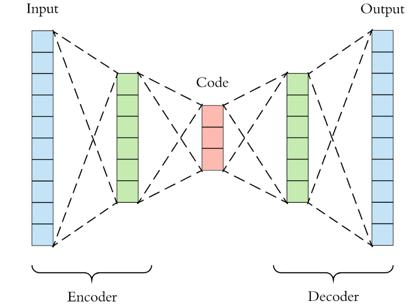
網(wǎng)絡(luò)背后的數(shù)學(xué)原理理解起來相對容易。從本質(zhì)上看,可以把網(wǎng)絡(luò)分成兩個部分:編碼器和解碼器。
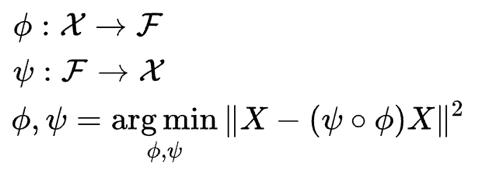
編碼器函數(shù)用ϕ表示,該函數(shù)將原始數(shù)據(jù)X映射到潛在空間F中(潛在空間F位于瓶頸處)。解碼器函數(shù)用ψ表示,該函數(shù)將瓶頸處的潛在空間F映射到輸出函數(shù)。此處的輸出函數(shù)與輸入函數(shù)相同。因此,我們基本上是在一些概括的非線性壓縮之后重建原始圖像。
編碼網(wǎng)絡(luò)可以用激活函數(shù)傳遞的標(biāo)準(zhǔn)神經(jīng)網(wǎng)絡(luò)函數(shù)表示,其中z是潛在維度。
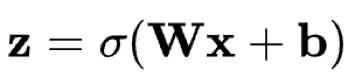
相似地,解碼網(wǎng)絡(luò)可以用相同的方式表示,但需要使用不同的權(quán)重、偏差和潛在的激活函數(shù)。
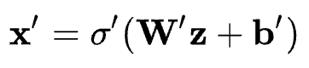
隨后就可以利用這些網(wǎng)絡(luò)函數(shù)來編寫損失函數(shù),我們會利用這個損失函數(shù)通過標(biāo)準(zhǔn)的反向傳播程序來訓(xùn)練神經(jīng)網(wǎng)絡(luò)。
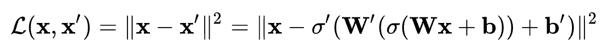
由于輸入和輸出的是相同的圖像,神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程并不是監(jiān)督學(xué)習(xí)或無監(jiān)督學(xué)習(xí),我們通常將這個過程稱為自我監(jiān)督學(xué)習(xí)。自動編碼器的目的是選擇編碼器和解碼器函數(shù),這樣就可以用最少的信息來編碼圖像,使其可以在另一側(cè)重新生成。
如果在瓶頸層中使用的節(jié)點太少,重新創(chuàng)建圖像的能力將受到限制,導(dǎo)致重新生成的圖像模糊或者和原圖像差別很大。如果使用的節(jié)點太多,那么就沒必要壓縮了。
壓縮背后的理論其實很簡單,例如,每當(dāng)你在Netflix下載某些內(nèi)容時,發(fā)送給你的數(shù)據(jù)都會被壓縮。一旦這個內(nèi)容傳輸?shù)诫娔X上就會通解壓算法在電腦屏幕顯示出來。這類似于zip文件的運行方式,只是這里說的壓縮是在后臺通過流處理算法完成的。
去噪自動編碼器
有幾種其它類型的自動編碼器。其中最常用的是去噪自動編碼器,本教程稍后會和Keras一起進(jìn)行分析。這些自動編碼器在訓(xùn)練前給數(shù)據(jù)添加一些白噪聲,但在訓(xùn)練時會將誤差與原始圖像進(jìn)行比較。這就使得網(wǎng)絡(luò)不會過度擬合圖像中出現(xiàn)的任意噪聲。稍后,將使用它來清除文檔掃描圖像中的折痕和暗黑區(qū)域。
稀疏自動編碼器
與其字義相反的是,稀疏自動編碼器具有比輸入或輸出維度更大的潛在維度。然而,每次網(wǎng)絡(luò)運行時,只有很小一部分神經(jīng)元會觸發(fā),這意味著網(wǎng)絡(luò)本質(zhì)上是“稀疏”的。稀疏自動編碼器也是通過一種規(guī)則化的形式來減少網(wǎng)絡(luò)過度擬合的傾向,這一點與去噪自動編碼器相似。
收縮自動編碼器
收縮編碼器與前兩個自動編碼器的運行過程基本相同,但是在收縮自動編碼器中,我們不改變結(jié)構(gòu),只是在丟失函數(shù)中添加一個正則化器。這可以被看作是嶺回歸的一種神經(jīng)形式。
現(xiàn)在了解了自動編碼器是如何運行的,接下來看看自動編碼器的弱項。一些最顯著的挑戰(zhàn)包括:
· 潛在空間中的間隙
· 潛在空間中的可分性
· 離散潛在空間
這些問題都在以下圖中體現(xiàn)。
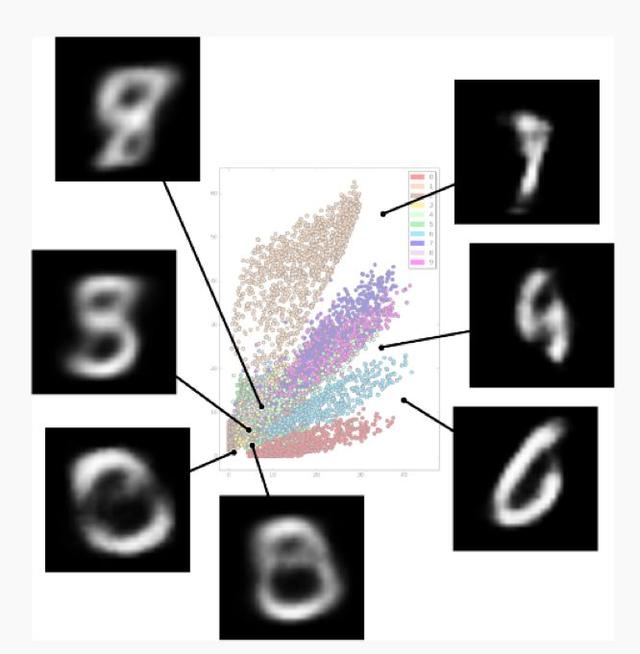
MNIST數(shù)據(jù)集的潛在空間表示
這張圖顯示了潛在空間中不同標(biāo)記數(shù)字的位置。可以看到潛在空間中存在間隙,我們不知道字符在這些空間中是長什么樣的。這相當(dāng)于在監(jiān)督學(xué)習(xí)中缺乏數(shù)據(jù),因為網(wǎng)絡(luò)并沒有針對這些潛在空間的情況進(jìn)行過訓(xùn)練。另一個問題就是空間的可分性,上圖中有幾個數(shù)字被很好地分離,但也有一些區(qū)域被標(biāo)簽字符是隨機分布的,這讓我們很難區(qū)分字符的獨特特征(在這個圖中就是數(shù)字0-9)。還有一個問題是無法研究連續(xù)的潛在空間。例如,我們沒有針對任意輸入而訓(xùn)練的統(tǒng)計模型(即使我們填補了潛在空間中的所有間隙也無法做到)。
這些傳統(tǒng)自動編碼器的問題意味著我們還要做出更多努力來學(xué)習(xí)數(shù)據(jù)生成分布并生成新的數(shù)據(jù)與圖像。
現(xiàn)在已經(jīng)了解了傳統(tǒng)自動編碼器是如何運行的,接下來討論變分自動編碼器。變分自動編碼器采用了一種從貝葉斯統(tǒng)計中提取的變分推理形式,因此會比前幾種自動編碼器稍微復(fù)雜一些。我們會在下一節(jié)中更深入地討論變分自動編碼器。
變分自動編碼器
變分自動編碼器延續(xù)了傳統(tǒng)自動編碼器的結(jié)構(gòu),并利用這一結(jié)構(gòu)來學(xué)習(xí)數(shù)據(jù)生成分布,這讓我們可以從潛在空間中隨機抽取樣本。然后,可以使用解碼器網(wǎng)絡(luò)對這些隨機樣本進(jìn)行解碼,以生成獨特的圖像,這些圖像與網(wǎng)絡(luò)所訓(xùn)練的圖像具有相似的特征。
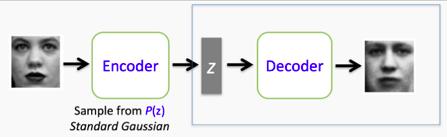
對于熟悉貝葉斯統(tǒng)計的人來說,編碼器正在學(xué)習(xí)后驗分布的近似值。這種分布通常很難分析,因為它沒有封閉式的解。這意味著我們要么執(zhí)行計算上復(fù)雜的采樣程序,如馬爾可夫鏈蒙特卡羅(MCMC)算法,要么采用變分方法。正如你可能猜測的那樣,變分自動編碼器使用變分推理來生成其后驗分布的近似值。
我們將會用適量的細(xì)節(jié)來討論這一過程,但是如果你想了解更深入的分析,建議你閱覽一下Jaan Altosaar撰寫的博客。變分推理是研究生機器學(xué)習(xí)課程或統(tǒng)計學(xué)課程的一個主題,但是了解其基本概念并不需要擁有一個統(tǒng)計學(xué)學(xué)位。
若對背后的數(shù)學(xué)理論不感興趣,也可以選擇跳過這篇變分自動編碼器(VAE)編碼教程。
首先需要理解的是后驗分布以及它無法被計算的原因。先看看下面的方程式:貝葉斯定理。這里的前提是要知道如何從潛變量“z”生成數(shù)據(jù)“x”。這意味著要搞清p(z|x)。然而,該分布值是未知的,不過這并不重要,因為貝葉斯定理可以重新表達(dá)這個概率。但是這還沒有解決所有的問題,因為分母(證據(jù))通常很難解。但也不是就此束手無辭了,還有一個挺有意思的辦法可以近似這個后驗分布值。那就是將這個推理問題轉(zhuǎn)化為一個優(yōu)化問題。
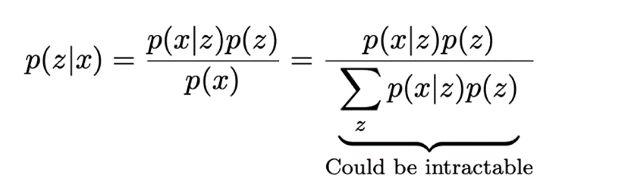
要近似后驗分布值,就必須找出一個辦法來評估提議分布與真實后驗分布相比是否更好。而要這么做,就需要貝葉斯統(tǒng)計員的最佳伙伴:KL散度。KL散度是兩個概率分布相似度的度量。如果它們相等,那散度為零;而如果散度是正值,就代表這兩個分布不相等。KL散度的值為非負(fù)數(shù),但實際上它不是一個距離,因為該函數(shù)不具有對稱性。可以采用下面的方式使用KL散度:
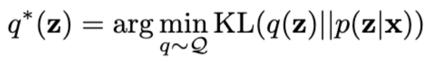
這個方程式看起來可能有點復(fù)雜,但是概念相對簡單。那就是先猜測可能生成數(shù)據(jù)的方式,并提出一系列潛在分布Q,然后再找出最佳分布q*,從將提議分布和真實分布的距離最小化,然后因其難解性將其近似。但這個公式還是有一個問題,那就是p(z|x)的未知值,所以也無法計算KL散度。那么,應(yīng)該怎么解決這個問題呢?
這里就需要一些內(nèi)行知識了。可以先進(jìn)行一些計算上的修改并針對證據(jù)下界(ELBO)和p(x)重寫KL散度:
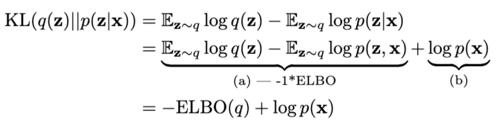
有趣的是ELBO是這個方程中唯一取決于所選分布的變量。而后者由于不取決于q,則不受所選分布的影響。因此,可以在上述方程中通過將ELBO(負(fù)值)最大化來使KL散度最小化。這里的重點是ELBO可以被計算,也就是說現(xiàn)在可以進(jìn)行一個優(yōu)化流程。
所以現(xiàn)在要做的就是給Q做一個好的選擇,再微分ELBO,將其設(shè)為零,然后就大功告成了。可是開始的時候就會面臨一些障礙,即必須選擇最好的分布系列。
一般來說,為了簡化定義q的過程,會進(jìn)行平均場變分推理。每個變分參數(shù)實質(zhì)上是相互獨立的。因此,每個數(shù)據(jù)點都有一個單獨的q,可被相稱以得到一個聯(lián)合概率,從而獲得一個“平均場”q。
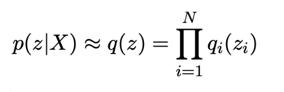
實際上,可以選用任意多的場或者集群。比如在MINIST數(shù)據(jù)集中,可以選擇10個集群,因為可能有10個數(shù)字存在。
要做的第二件事通常被稱為再參數(shù)化技巧,通過把隨機變量帶離導(dǎo)數(shù)完成,因為從隨機變量求導(dǎo)數(shù)的話會由于它的內(nèi)在隨機性而產(chǎn)生較大的誤差。
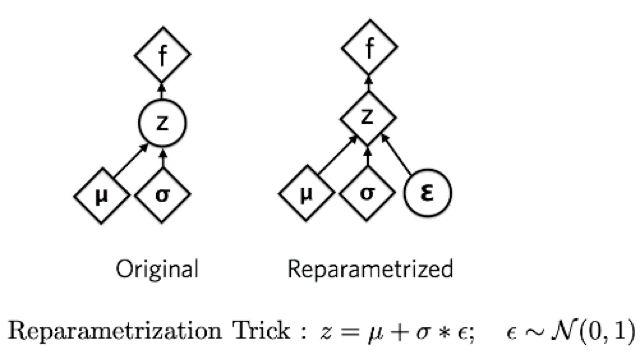
再參數(shù)化技巧較為深奧,但簡單來說就是可以將一個正態(tài)分布寫成均值加標(biāo)準(zhǔn)差,再乘以誤差。這樣在微分時,我們不是從隨機變量本身求導(dǎo)數(shù),而是從它的參數(shù)求得。
這個程序沒有一個通用的閉型解,所以近似后驗分布的能力仍然受到一定限制。然而,指數(shù)分布族確實有一個閉型解。這意味著標(biāo)準(zhǔn)分布,如正態(tài)分布、二項分布、泊松分布、貝塔分布等。所以,就算真正的后驗分布值無法被查出,依然可以利用指數(shù)分布族得出最接近的近似值。
變分推理的奧秘在于選擇分布區(qū)Q,使其足夠大以求得后驗分布的近似值,但又不需要很長時間來計算。
既然已經(jīng)大致了解如何訓(xùn)練網(wǎng)絡(luò)學(xué)習(xí)數(shù)據(jù)的潛在分布,那么現(xiàn)在可以探討如何使用這個分布生成數(shù)據(jù)。
數(shù)據(jù)生成過程
觀察下圖,可以看出對數(shù)據(jù)生成過程的近似認(rèn)為應(yīng)生成數(shù)字‘2’,所以它從潛在變量質(zhì)心生成數(shù)值2。但是也許不希望每次都生成一摸一樣的數(shù)字‘2’,就好像上述端游例子所提的植物,所以我們根據(jù)一個隨機數(shù)和“已學(xué)”的數(shù)值‘2’分布范圍,在潛在空間給這一過程添加了一些隨機噪聲。該過程通過解碼器網(wǎng)絡(luò)后,我們得到了一個和原型看起來不一樣的‘2’。
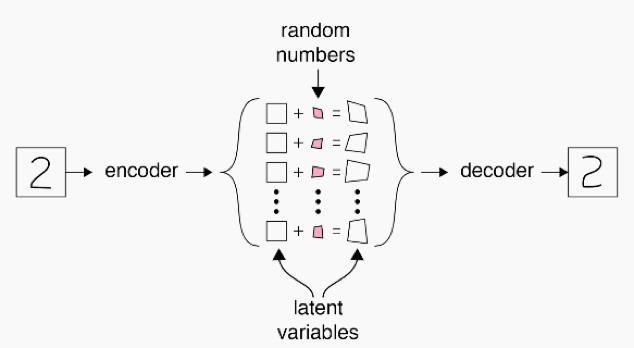
這是一個非常簡化的例子,抽象描述了實際自動編碼器網(wǎng)絡(luò)的體系結(jié)構(gòu)。下圖表示了一個真實變分自動編碼器在其編碼器和解碼器網(wǎng)絡(luò)使用卷積層的結(jié)構(gòu)體系。從這里可以觀察到,我們正在分別學(xué)習(xí)潛在空間中生成數(shù)據(jù)分布的中心和范圍,然后從這些分布“抽樣”生成本質(zhì)上“虛假”的數(shù)據(jù)。

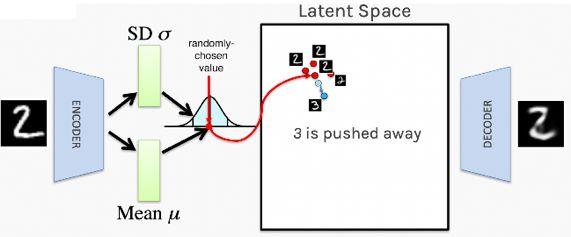
該學(xué)習(xí)過程的固有性代表所有看起來很相似的參數(shù)(刺激相同的網(wǎng)絡(luò)神經(jīng)元放電)都聚集到潛在空間中,而不是隨意的分散。如下圖所示,可以看到數(shù)值2都聚集在一起,而數(shù)值3都逐漸地被推開。這一過程很有幫助,因為這代表網(wǎng)絡(luò)并不會在潛在空間隨意擺放字符,從而使數(shù)值之間的轉(zhuǎn)換更有真實性。
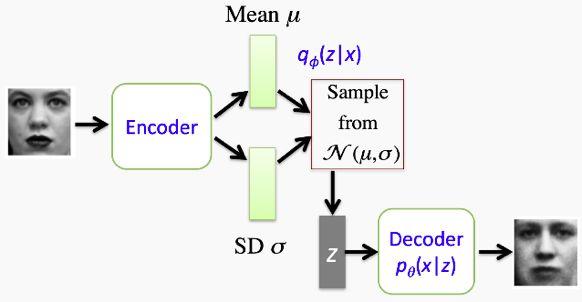
整個網(wǎng)絡(luò)體系結(jié)構(gòu)的概述如下圖所示。希望讀者看到這里,可以比較清晰地理解整個過程。我們使用一組圖像訓(xùn)練自動編碼器,讓它學(xué)習(xí)潛在空間里均值和標(biāo)準(zhǔn)值的差,從而形成我們的數(shù)據(jù)生成分布。接下來,當(dāng)我們要生成一個類似的圖像,就從潛在空間的一個質(zhì)心取樣,利用標(biāo)準(zhǔn)差和一些隨機誤差對它進(jìn)行輕微的改變,然后使其通過解碼器網(wǎng)絡(luò)。從這個例子可以明顯看出,最終的輸出看起來與輸入圖像相似,但卻是不一樣的。
變分自動編碼器編碼指南
本節(jié)將討論一個簡單的去噪自動編碼器,用于去除文檔掃描圖像上的折痕和污痕,以及去除Fashion MNIST數(shù)據(jù)集中的噪聲。然后,在MNIST數(shù)據(jù)集訓(xùn)練網(wǎng)絡(luò)后,就使用變分自動編碼器生成新的服裝。
去噪自編碼器
Fashion MNIST
在第一個練習(xí)中,在Fashion MNIST數(shù)據(jù)集添加一些隨機噪聲(椒鹽噪聲),然后使用去噪自編碼器嘗試移除噪聲。首先進(jìn)行預(yù)處理:下載數(shù)據(jù),調(diào)整數(shù)據(jù)大小,然后添加噪聲。
- ## Download the data
- (x_train, y_train), (x_test, y_test) = datasets.fashion_mnist.load_data()
- ## normalize and reshape
- x_train = x_train/255.
- x_test = x_test/255.
- x_train = x_train.reshape(-1, 28, 28, 1)
- x_test = x_test.reshape(-1, 28, 28, 1)
- # Lets add sample noise - Salt and Pepper
- noise = augmenters.SaltAndPepper(0.1)
- seq_object = augmenters.Sequential([noise])
- train_x_n = seq_object.augment_images(x_train * 255) / 255
- val_x_n = seq_object.augment_images(x_test * 255) / 255
接著,給自編碼器網(wǎng)絡(luò)創(chuàng)建結(jié)構(gòu)。這包括多層卷積神經(jīng)網(wǎng)絡(luò)、編碼器網(wǎng)絡(luò)的最大池化層和解碼器網(wǎng)絡(luò)上的升級層。
- # input layer
- input_layer =Input(shape=(28, 28, 1))
- # encodingarchitecture
- encoded_layer1= Conv2D(64, (3, 3), activation='relu', padding='same')(input_layer)
- encoded_layer1= MaxPool2D( (2, 2), padding='same')(encoded_layer1)
- encoded_layer2= Conv2D(32, (3, 3), activation='relu', padding='same')(encoded_layer1)
- encoded_layer2= MaxPool2D( (2, 2), padding='same')(encoded_layer2)
- encoded_layer3= Conv2D(16, (3, 3), activation='relu', padding='same')(encoded_layer2)
- latent_view = MaxPool2D( (2, 2),padding='same')(encoded_layer3)
- # decodingarchitecture
- decoded_layer1= Conv2D(16, (3, 3), activation='relu', padding='same')(latent_view)
- decoded_layer1= UpSampling2D((2, 2))(decoded_layer1)
- decoded_layer2= Conv2D(32, (3, 3), activation='relu', padding='same')(decoded_layer1)
- decoded_layer2= UpSampling2D((2, 2))(decoded_layer2)
- decoded_layer3= Conv2D(64, (3, 3), activation='relu')(decoded_layer2)
- decoded_layer3= UpSampling2D((2, 2))(decoded_layer3)
- output_layer = Conv2D(1, (3, 3), padding='same',activation='sigmoid')(decoded_layer3)
- # compile themodel
- model =Model(input_layer, output_layer)
- model.compile(optimizer='adam',loss='mse')
- # run themodel
- early_stopping= EarlyStopping(monitor='val_loss', min_delta=0, patience=10, verbose=5,mode='auto')
- history =model.fit(train_x_n, x_train, epochs=20, batch_size=2048,validation_data=(val_x_n, x_test), callbacks=[early_stopping])
所輸入的圖像,添加噪聲的圖像,和輸出圖像。

從時尚MNIST輸入的圖像。

添加椒鹽噪聲的輸入圖像。

從去噪網(wǎng)絡(luò)輸出的圖像。
從這里可以看到,我們成功從噪聲圖像去除相當(dāng)?shù)脑肼暎瑫r也失去了一定量的服裝細(xì)節(jié)的分辨率。這是使用穩(wěn)健網(wǎng)絡(luò)所需付出的代價之一。可以對該網(wǎng)絡(luò)進(jìn)行調(diào)優(yōu),使最終的輸出更能代表所輸入的圖像。
文本清理
去噪自編碼器的第二個例子包括清理掃描圖像的折痕和暗黑區(qū)域。這是最終獲得的輸入和輸出圖像。

輸入的有噪聲文本數(shù)據(jù)圖像。

經(jīng)清理的文本圖像。
為此進(jìn)行的數(shù)據(jù)預(yù)處理稍微復(fù)雜一些,因此就不在這里進(jìn)行介紹,預(yù)處理過程和相關(guān)數(shù)據(jù)可在GitHub庫里獲取。網(wǎng)絡(luò)結(jié)構(gòu)如下:
- input_layer= Input(shape=(258, 540, 1))
- #encoder
- encoder= Conv2D(64, (3, 3), activation='relu', padding='same')(input_layer)
- encoder= MaxPooling2D((2, 2), padding='same')(encoder)
- #decoder
- decoder= Conv2D(64, (3, 3), activation='relu', padding='same')(encoder)
- decoder= UpSampling2D((2, 2))(decoder)
- output_layer= Conv2D(1, (3, 3), activation='sigmoid', padding='same')(decoder)
- ae =Model(input_layer, output_layer)
- ae.compile(loss='mse',optimizer=Adam(lr=0.001))
- batch_size= 16
- epochs= 200
- early_stopping= EarlyStopping(monitor='val_loss',min_delta=0,patience=5,verbose=1,mode='auto')
- history= ae.fit(x_train, y_train, batch_size=batch_size, epochs=epochs,validation_data=(x_val, y_val), callbacks=[early_stopping])
變分自編碼器
最后的壓軸戲,是嘗試從FashionMNIST數(shù)據(jù)集現(xiàn)有的服裝中生成新圖像。
其中的神經(jīng)結(jié)構(gòu)較為復(fù)雜,包含了一個稱‘Lambda’層的采樣層。
- batch_size = 16
- latent_dim = 2 # Number of latent dimension parameters
- # ENCODER ARCHITECTURE: Input -> Conv2D*4 -> Flatten -> Dense
- input_img = Input(shape=(28, 28, 1))
- x = Conv2D(32, 3,
- padding='same',
- activation='relu')(input_img)
- x = Conv2D(64, 3,
- padding='same',
- activation='relu',
- strides=(2, 2))(x)
- x = Conv2D(64, 3,
- padding='same',
- activation='relu')(x)
- x = Conv2D(64, 3,
- padding='same',
- activation='relu')(x)
- # need to know the shape of the network here for the decoder
- shape_before_flattening = K.int_shape(x)
- x = Flatten()(x)
- x = Dense(32, activation='relu')(x)
- # Two outputs, latent mean and (log)variance
- z_mu = Dense(latent_dim)(x)
- z_log_sigma = Dense(latent_dim)(x)
- ## SAMPLING FUNCTION
- def sampling(args):
- z_mu, z_log_sigma = args epsilon = K.random_normal(shape=(K.shape(z_mu)[0], latent_dim),
- mean=0., stddev=1.)
- return z_mu + K.exp(z_log_sigma) * epsilon
- # sample vector from the latent distribution
- z = Lambda(sampling)([z_mu, z_log_sigma])
- ## DECODER ARCHITECTURE
- # decoder takes the latent distribution sample as input
- decoder_input = Input(K.int_shape(z)[1:])
- # Expand to 784 total pixels
- x = Dense(np.prod(shape_before_flattening[1:]),
- activation='relu')(decoder_input)
- # reshape
- x = Reshape(shape_before_flattening[1:])(x)
- # use Conv2DTranspose to reverse the conv layers from the encoder
- x = Conv2DTranspose(32, 3,
- padding='same',
- activation='relu',
- strides=(2, 2))(x)
- x = Conv2D(1, 3,
- padding='same',
- activation='sigmoid')(x)
- # decoder model statement
- decoder = Model(decoder_input, x)
- # apply the decoder to the sample from the latent distribution
- z_decoded = decoder(z)
這就是體系結(jié)構(gòu),但還是需要插入損失函數(shù)再合并KL散度。
- # construct a custom layer to calculate the loss
- class CustomVariationalLayer(Layer):
- def vae_loss(self, x, z_decoded):
- x = K.flatten(x)
- z_decoded = K.flatten(z_decoded)
- # Reconstruction loss
- xent_loss = binary_crossentropy(x, z_decoded)
- # KL divergence
- kl_loss = -5e-4 * K.mean(1 + z_log_sigma - K.square(z_mu) - K.exp(z_log_sigma), axis=-1)
- return K.mean(xent_loss + kl_loss)
- # adds the custom loss to the class
- def call(self, inputs):
- x = inputs[0]
- z_decoded = inputs[1]
- loss = self.vae_loss(x, z_decoded)
- self.add_loss(loss, inputs=inputs)
- return x
- # apply the custom loss to the input images and the decoded latent distribution sample
- y = CustomVariationalLayer()([input_img, z_decoded])
- # VAE model statement
- vae = Model(input_img, y)
- vae.compile(optimizer='rmsprop', loss=None)
- vae.fit(x=train_x, y=None,
- shuffle=True,
- epochs=20,
- batch_size=batch_size,
- validation_data=(val_x, None))
現(xiàn)在,可以查看重構(gòu)的樣本,看看網(wǎng)絡(luò)能夠?qū)W習(xí)到什么。

從這里可以清楚看到鞋子、手袋和服裝之間的過渡。在此并沒有標(biāo)出所有使畫面更清晰的潛在空間。也可以觀察到Fashion MNIST數(shù)據(jù)集現(xiàn)有的10件服裝的潛在空間和顏色代碼。
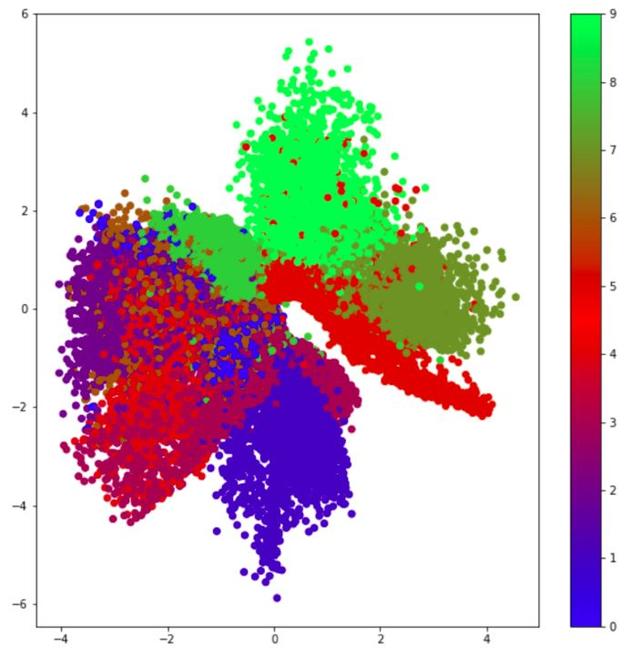
可看出這些服飾分成了不同的集群。