想要去谷歌、Facebook、蘋果這樣的公司工作嗎?很多時候它們的面試會讓人望而卻步。不用害怕，我們已經掌握了它們的常規面試題。近日，麻省理工學院(MIT)計算機科學和人工智能實驗室(CSAIL)的新版「程序員面試課程」資料已被公開。無論你是初級程序員還是經驗豐富的專家，這門課程都適合你。

課程鏈接：http://courses.csail.mit.edu/iap/interview/index.php

本課程重點介紹科技公司在面試時經常出現的計算機科學問題，其中包括時間復雜度、哈希表、二進制樹搜索，以及 MIT「算法設計與分析」(MIT 6.046)課程中會出現的內容。但是，大部分時間都會專注于你不會在課堂上學到的內容，例如刁鉆的按位邏輯和解決問題的技巧。

面試錦囊

被問到一個問題時，要和面試官展開對話，讓對方知道你在思考。例如，你可能會提供一個較慢或能解決部分問題的方案(讓他們知道這個方案并不***)，提到一些關于這個問題的觀察結果，或者說一下任何有可能對解決問題有幫助的想法。如果你卡住了，面試官通常會給你點提示。

面試期間，你通常會被要求寫一個程序。出于某種原因，面試官通常讓人在黑板或紙上寫，而不是給你一臺電腦。所以，有必要在面試之前練一下在板子上寫代碼，以備不時之需。

以下是編程面試中的一些注意事項：

這些事要做：

• 如果對問題有哪里不理解或有歧義，一定要問清楚;
• 讓面試官知道你在想什么;
• 針對問題提出多個解決方案;
• 與面試官交流想法(如關于數據結構和算法的想法)
• 如果你卡住了，不要害怕讓他們知道，可以禮貌地尋求提示。

這些事不要做：

• 不要放棄!放棄對你展示自己的問題解決技巧沒有任何幫助;
• 思考期間不要只是安靜地坐在那里。面試官要在有限的時間內盡可能多地了解你，不和他們交流無法向他們傳遞任何信息;
• 如果你已經知道問題的答案，不要脫口而出!不然他們會覺得你提前看過這個問題并記下了答案。至少要在給出答案之前假裝思考一陣兒。

好了，如果你對自己的備考情況很有信心，以下是其中的一些經典問題：

問題 1：硬幣難題

假設你有 8 枚大小相同的硬幣，但其中 1 枚硬幣要比其他 7 枚稍重一點(但你不知道具體是哪一枚)。同時，你還有一個老式天平可以稱重，從而得出哪枚硬幣稍重(或是否重量相同)。那么，最少要稱多少次才能找出那枚稍輕的硬幣?

優秀答案：從 8 枚硬幣中取出 6 枚，天平左右盤各放 3 枚。結果會出現三種情況：天平左盤 3 枚硬幣重于右盤，則較重的 1 枚在左盤;天平右盤的 3 枚硬幣重于左盤，則較重的 1 枚在右盤;天平左右盤重量相等，則稱剩下的 2 枚硬幣，得出稍重的這枚硬幣。

不太好的答案：分別取 4 枚硬幣放置于天平左右盤，找出較輕的一組(4 枚)，將該組硬幣繼續分為兩組放入天平左右盤，找出較輕的一組(2 枚)，再次重復此步驟找到最輕的一枚。

問題 2：在數組中進行查找

給定一個已排序的整數數組，如何找出特定整數 x 的位置?

優秀答案：使用二分搜索法。將數組中間的數字與 x 進行比較。如果相同，則找出了 x。如果數組中的數字較大，則需要查看數組后半部分。如果數字較小，則需要查看數組前半部分。通過比較數組中間元素和 x，我們可以重復搜索該數組的前后部分，從而再次將搜索范圍縮小 2 倍。我們重復這一過程直至找出 x。這種算法花費的時間為 O(log n)。

不太好的答案：按順序查看數組的每個數字，與 x 進行比較。這種算法花費的時間為 O(n)。

問題 3：A to I

編寫一個函數將字符串轉換為整數(這個函數被稱為 A to I 或者 atoi())，因為我們要將一個 ASCII 字符串轉換為整數。

優秀答案：從頭到尾查看整個字符串。如果***字符為負號，記下來。從 0 開始進行累計求和。每得到一個新數字，總數乘以 10 并加上這個新數字。當計算結束時，返回當前總數，或者如果出現負號，返回該數字的倒數。

湊合的答案：另一種方法也是從頭到尾查看整個字符串，再次進行累計求和。記住表示當前你所在數字的數字 x，x 最開始為 1。針對每個字符，將當前數字乘以 x 并添加到累計總數中，同時將 x 乘以 10。當你到達字符串起點時，返回當前總數，或者如果出現負號，返回該數字的倒數。

注意：面試官可能會詢問你自身方法的局限性。你應該回答：只有字符串在每個數字前都包含可選負號時，該方法才能生效。同時，你還應提到：如果數字太大，則結果會因為溢值原因而不正確。

問題 4：顛倒字符串中的單詞順序

編寫一個函數將字符串中的單詞順序進行顛倒。

答案：交換***個與倒數***個、第二個與倒數第二個字符的順序，以此類推，顛倒整個字符串。之后，查看整個字符串，找出空格，這樣就可以發現每個單詞的位置。再次交換***個與倒數***個、第二個與倒數第二個單詞的順序，以此類推，顛倒你所遇到的每個單詞的順序。

問題 5：最近鄰

假設你有一個包含 n 個人信息的數組。每個人分別用一個字符串(他們的名字)和一個數字(他們在數軸上的位置)表示。每個人有三個朋友，即數字和他本人最接近的三個人。請寫出一個可以找出每個人的三個朋友的算法。

優秀答案：按每個人數字的升序對數組進行排列。查看每個人前后緊鄰的三個人，他們的朋友將出現在這六個人當中。這一算法花費的時間為 O(n log n)，因為將人進行分類也會花費那么多時間。

問題 6：洗牌問題

給定一組不同的整數數組，給出一個算法對這些整數進行隨機排序，使每個重排序方法的可能性相等。換句話說，給定一副牌，你要如何洗牌才能確保牌的每種排列方法有相同的可能?

優秀答案：按順序排列這些元素，用數組中不先于某個元素出現的隨機元素與該元素進行交換。需要的時間為 O(n)。

注意，這個問題有多個可能的答案，也有幾種看似不錯但實際上并不正確的答案。例如，對上面的算法做一個小小的修改，即，將每個元素與數組中的任意一個元素交換并不能確保每種重排順序等概率出現。這里給出的答案(在作者看來)是***答案。如果想了解其他答案，可以在維基百科上搜一下「Shuffling」。

問題 7：單鏈表中的循環

如何確定單鏈表是否有循環?

優秀答案：跟蹤鏈表中的兩個指針，并在鏈表的開始處啟動它們。在算法的每輪迭代中，將***個指針往前移一個節點，把第二個指針往前移兩個節點。如果兩個指針始終相同(不是在算法起點處)，那么就有一個循環。如果指針在兩個指針相同之前就達到鏈表的末端，鏈表中就沒有循環。其實，指針不需要一次移動一到兩個節點;指針也不需要以不同的速率移動。這個過程需要的時間為 O(n)。這是一個巧妙的回答，面試官會莫名喜歡。

湊合的回答 1：對于你在逐一瀏覽鏈表時遇到的每個節點，將指向該節點的指針放入 O(1) 中——查找時間數據結構，如散列集。接下來，當你遇到一個新的節點時，要看看指向那個節點的指針是否已經存在于你的散列集中。這一過程花費的時間為 O(n)，但占用的空間也是 O(n)。

湊合的回答 2：瀏覽鏈表中的元素。「Mark」你到達的每個節點。如果在抵達末端之前你到達了一個 mark 過的節點，列表中就有循環，否則就沒有循環。這一過程花費的時間也是 O(n)。

注意，這個問題在技術上是不恰當的。一個普通的鏈表不會有循環。他們的意思是讓你決定能否從一個圖中的節點到達循環，該圖包含最多有一條輸出邊的節點。

問題 8：計算 2^x

如何快速計算 2^x?

優秀答案：1 << x (1 left‐shifted by x)

問題 9：二叉搜索樹

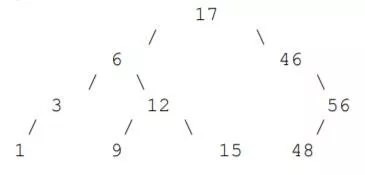
二叉搜索樹是一種排序保存項目的數據結構，它由二叉樹組成。每個節點都有一個指向兩個子節點的指針(可能為 null)，一個指向其父節點的可選指針(也可以為 null)，以及一個存儲在樹中的元素(可能是一個字符串或一個整數)。要使二叉搜索樹有效，每個節點的元素必須大于其左子樹中的每個元素，并且小于其右子樹中的每個元素。例如，二叉樹可能如下所示：

要檢查元素是否出現在二叉搜索樹中，只需要遵循父對子之間的相應連接。例如，如果我們想在上面的樹中搜索 15，我們從最上方的 17 開始。由于 15<17，我們移動到左邊的節點 6。由于 15> 6，我們移動到右邊的節點 12;由于 15>12，我們再次移動到正確的節點 15，最終找到了需要的數字。

要將元素加入二叉搜索樹，我們就要像搜索元素一樣，遵循從父節點到子節點的正確連接。當所需的子項為 null 時，我們將該元素添加為新的子節點。例如，如果我們要在上面的樹中添加 14，我們就需要不斷往下尋找添加的位置。當我們到達 15，就會看到該節點沒有左子節點，因此我們將 14 添加為左子節點。

要從二叉搜索樹中刪除一個元素，我們首先要找出包含該元素的節點。如果該節點沒有子節點，直接刪除即可。如果該節點有一個子節點，則用這個子節點替代它。如果該節點有兩個子節點，我們通過一種算法確定樹中下一個更小或下一個更大的元素。為簡單起見，這里就不贅述所使用的算法了。我們將節點中存儲的元素設定為該值。之后，我們從樹中拼接包含該值的節點。這個過程相對較容易，因為節點最多有一個子節點。例如，為了從樹中刪除 6，我們首先將節點值更改為 3。之后，我們刪除原本值為 3 的節點，并將原本值為 6 的節點的左子節點值設定為 1。

在二叉搜索樹上做小小的修改，就可以使用它將鍵與值關聯起來，就像在散列表中一樣。我們不需要在每個節點上存儲單個值，而是存儲一個鍵值對。該樹將根據節點的鍵進行排序。

面試官有時會問到二叉搜索樹的問題。此外，二叉搜索樹往往在回答面試問題時也很有用。需要記住的重要一點是，插入、刪除和查找需要的時間為 O(log n)，其中 n 是樹中的元素數量，因為一個平衡良好的二叉搜索樹的高度是 O(log n)。盡管在最糟糕的情況下，一個二叉搜索樹的高度可能為 O(n)，「自平衡」二叉搜索樹可以周期性地重組一個 BST 來確保其高度為 O(log n)。許多自平衡 BST 保證這些操作花費的時間為 O(log n)。

問題 10：排除 bug

描述一種從程序中找出 bug 的方法。

答案：這個問題有多個可能的答案，也是面試官經常會問的開放性問題。優秀答案可能包括：根據程序的行為判斷可能出現 bug 的部分;使用斷點和 stepper 逐步執行程序。任何試圖找到 bug 源頭和縮小 bug 搜索范圍的方法都是好答案。

以上是谷歌程序員面試時可能出現的編程題及解題技巧。當然，只是其中很小的一部分。

• 想要了解更多問題和答案請點擊：http://courses.csail.mit.edu/iap/interview/materials.phpMIT《算法設計與分析》課程資料：
• https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2015/

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】 

戳這里，看該作者更多好文