什么?神經網絡還能創造新知識?
神經網絡(NNs)可以在不知道用顯式算法執行工作的情況下被設計和訓練于特定的任務,很多人都對此表示驚嘆。例如,著名的手寫體數字識別教程很容易執行,但其背后的邏輯還是隱藏在神經網絡下,僅能通過層次化結構、權值和激活函數略知一二。
圖片來源:Unsplash
本文通過神經網絡透明原則來揭示其“黑盒知識”,為此來檢驗一個布爾異或函數的神經網絡。首先,利用已知異或屬性過程構造了一個自底向上的神經網絡,即清晰包含已知的代數關系。在第二步中使用TensorFlow Keras從簡易圖形化編程工具到異或邏輯運算訓練神經網絡。
***比較兩種方法。將Keras神經網絡分解為布爾組件,發現邏輯設置與***步中構造的神經網絡不同。被訓練的神經網絡發現了使用不同布爾函數的另一種異或運算表示方法。
這另一種異或公式在數學領域不是未知的,但至少很新奇。這或許表明神經網絡可以創造新的知識。但要提取它,必須能夠將神經網絡的設置和參數轉化為顯式規則。
自底向上構造異或運算神經網絡(XOR NN)
異或運算是由映射定義的布爾函數,
- XOR (0,0) = XOR (1,1) = 0
- XOR (1,0) = XOR (0,1) = 1
為異或運算構造一個已知的神經網絡或谷歌標識列
- XOR (x,y) = AND ( NAND (x,y) , OR (x,y) )
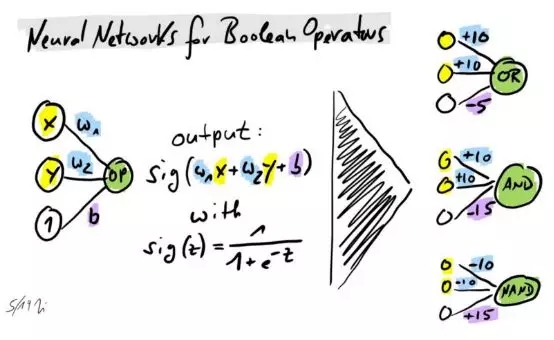
這很有幫助,因為操作符AND、NAND(而非AND)和OR是眾所周知的,并且都可以用簡單的神經網絡來表示,其中有2個輸入和1個輸出結點、偏移量和sigmoid激活函數。
布爾函數操作符的神經網絡
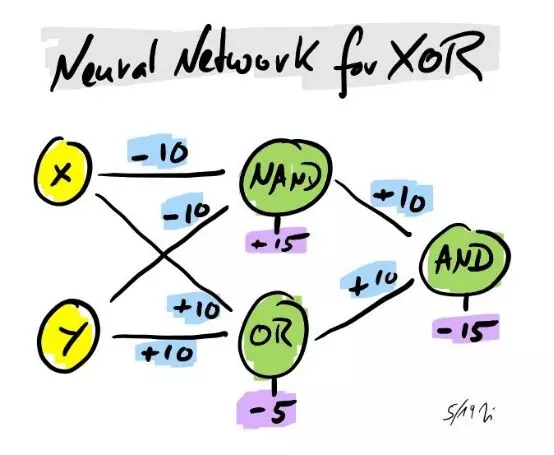
在此基礎上可通過連接NAND、AND和OR的NNs來構造異或運算神經網絡。所以異或變成了一個三層神經網絡。
異或運算的神經網絡
輸送可能的輸入配置并檢查輸出(本文使用Excel工作表)。分別得到有效的(0,0)、(1,1)的0.0072以及(0,1)、(1,0)的0.9924。
可以用以下異或運算的表示來建構其他的神經網絡:
- XOR (x,y) = OR ( AND ( NOT(x) , y ) , AND ( x , NOT(y) ) )
- XOR (x,y) = NAND ( NAND ( x , NAND ( x,y) ) , NAND ( y , NAND ( x,y) ) )
然而這些標識列導致了更復雜的網絡。
此外,由于異或運算不能通過線性可分(且激活函數嚴格單調),因此,不可能建立兩層的神經網絡。
但也許還有其他方法可以構建異或運算的神經網絡呢?下一節將通過訓練神經網絡來尋找另一種解決方案。
使用TensorFlow Keras構建異或神經網絡
Keras是一個功能強大且易于使用的神經網絡庫。上一節中建立了一個三層的2-2-1模型,并與之前建構的神經網絡進行了比較。
使用梯度下降優化器與學習率1和均方誤差損失函數的誤差反向傳播,這是建構神經網絡的標準方法。
以下是Python的代碼片段:
- # Generate NN for XOR operation
- # input layer: <NODES> nodes, one for each bit (0 = false and +1 = true)
- # output layer: 1 node for result (0 = false and +1 = true)
- # Use sigmoid activation function, gradient descent optimizer and mean squared error loss function
- # Last update: 28.05.2019
- import tensorflow as tf
- import numpy as np
- import matplotlib.pyplot as plt
- # Define model
- nodes = 2
- model = tf.keras.Sequential()
- model.add(tf.keras.layers.Dense(nodes, input_dim=2, activation=tf.nn.sigmoid))
- model.add(tf.keras.layers.Dense(1, activation=tf.nn.sigmoid))
- model.compile(optimizer=tf.train.GradientDescentOptimizer(1), loss=tf.keras.losses.mean_squared_error, metrics=['binary_accuracy'])
- model.summary()
- # Generate train & test data
- epochs = 10000
- data_in = np.array([[0,0],[0,1],[1,0],[1,1]])
- data_out = np.array([0,1,1,0])
- # Train model
- history = model.fit(data_in, data_out, epochsepochs=epochs, verbose=0)
- # Analysis of training history
- for key in history.history.keys():
- plt.scatter(range(epochs), history.history[key], s=1)
- plt.ylabel(key)
- plt.xlabel('epochs')
- plt.show()
- # Predict with model
- result = model.predict(data_in)
- # Print results
- def printarray(arr):
- return np.array2string(arr).replace('\n','')
- print()
- print('input', printarray(data_in))
- print('output (calculation)', printarray(data_out))
- print('output (prediction) ', printarray(result))
- print('output (pred. norm.)', printarray(np.round(result)))
- # Get weights of model
- print()
- print(model.get_weights())
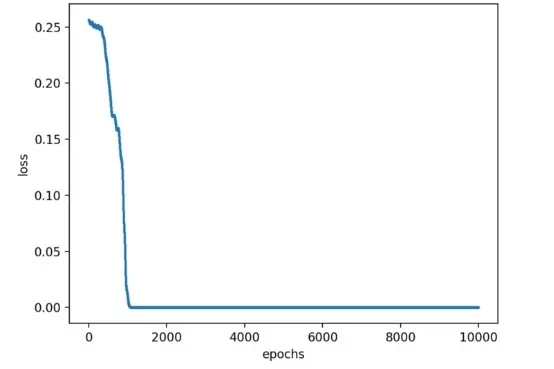
異或運算的好處是可以訓練整個參數空間,因為只有四種可能的配置可以教。然而,需要一些在神經網絡中傳遞數據集的過程來驅動模型達到零損耗和100%精準,即輸出趨向于一個分別是(0,1)、(1,0)和(0,0)、(1,1)的零。
異或運算神經網絡的Loss和epochs對比
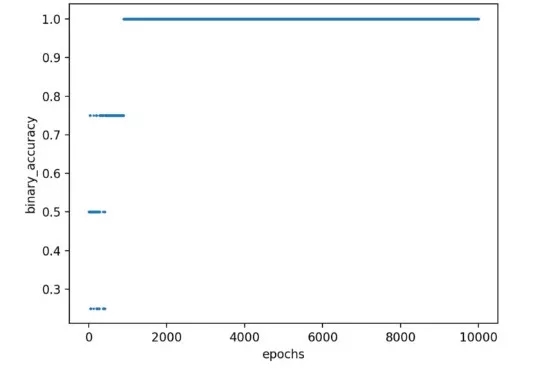
異或運算神經網絡的Accuracy 和epochs對比
然而,訓練期也可能陷入停滯,無法銜接。接著精準度停止在75%甚至50%,即一個或兩個二元元組的映射是不正確的。在這種情況下就要重新構建神經網絡,直到得到合適的解決方案。
分析和結論
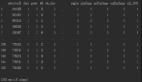
現在驗證Keras神經網絡是否與建構的具有相似結構。通過返回權值(參見代碼片段的末尾),得到了權值和偏差值。
Python的腳本輸出
使用這些參數來重建神經網絡(再次使用Excel)。由三個操作符組成。
基于Keras訓練的異或運算神經網絡
通過輸入所有可能的配置,可以識別與H1、H2和O操作符關聯的布爾函數。
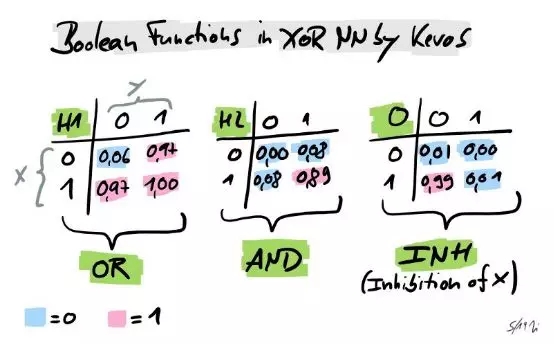
Keras在異或運算神經網絡中的布爾函數
有趣的是,本以為Keras 神經網絡與所建構的邏輯是一樣的,但它卻創建了另一種解決方案。使用OR,AND和(相對沒人知道的)INH,而非操作符NAND, OR 和AND,即神經網絡找到的公式。
- XOR (x,y) = INH ( OR (x,y), AND (x,y) )
這表明神經網絡可以獲得以前沒有的知識!當然“新知識”是相對的,并且取決于知道的程度。也就是說,若一個人知道異或運算的所有表示形式,Keras 神經網絡就不會有其他價值。
此外,對于更復雜的神經網絡,將權值轉換為顯式算法或公式并不容易。但也許這種專業知識是未來人工智能專家必須具備的能力。