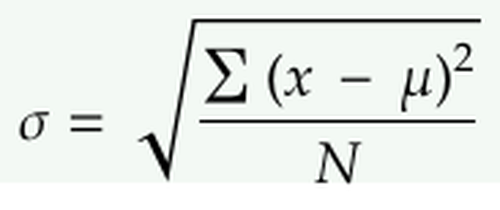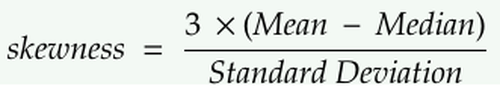數據科學實際上可以定義為我們從數據中獲取額外信息的一個過程，在做數據科學時，我們真正想要做的其實就是解釋除了數字之外，所有數據在現實世界中的實際含義。

為了提取潛藏在復雜數據集中的信息，數據科學家采用了許多工具和技術，包括數據挖掘、數據可視化和數據建模等等。數據挖掘中常用的一類非常重要的數學技術是統計學。

在實際意義上，統計數據允許我們定義數據的具體數學摘要。我們可以使用統計信息來描述其中的一些屬性，而不是嘗試描述每個數據點。而這通常足以讓我們提取有關數據結構和構成的某些信息。

[[269527]]

有些時候，當人們聽到“統計”這個詞時，往往會想到一些過于復雜的東西。也可能會有點抽象，但我們并非總是需要訴諸復雜的理論，來從統計中獲得某種價值。

統計學中最基本的部分通常是數據科學中最實用的部分。

今天，我們將分享5個對于數據科學有用的統計學方法。這些不是過分抽象的概念，而是相當簡單、有長期適用性的技術。

一、集中趨勢(Central Tendency)

數據集或特征變量的集中趨勢是集的中心或典型值。其思想是，可能有一個單一的值可以(在某種程度上)***地描述我們的數據集。

例如，假設你有一個以x-y位置(100,100)為中心的正態分布。那么點(100,100)是集中趨勢，因為在所有可選擇的點中，它提供了對數據***的總結。

對于數據科學來說，我們可以使用集中趨勢進行度量，來快速簡單地了解我們數據集的整體情況。我們的數據的“中心”可以是非常有價值的信息，它告訴我們數據集究竟是如何偏置的，因為數據所圍繞的任何值本質上都是偏置。

在數學上有兩種選擇集中趨勢的常用方法。

平均數(Mean)

平均數，也就是數據集的平均值，即整個數據圍繞其進行散布的一個數字。在定義平均數時，所有用于計算平均數的值的權重都是相等的。

例如，計算以下5個數字的平均數：

• (3 + 64 + 187 + 12 + 52)/ 5 = 63.6

平均數非常適合計算實際數學平均值，使用像Numpy這樣的Python庫計算速度也非常快。

中位數(Median)

中位數是數據集的中間值，即我們將數據從最小值排序到***值(或從***值到最小值)，然后取值集合中間的值：那就是中位數。

計算上一個例子中5個數字的中位數：

• [3，12，52，64，187]→ 52

中值與平均數完全不同。它們沒有對錯優劣之分，但我們可以根據我們的情況和目標選擇一個。

計算中位數需要對數據進行排序——如果數據集很大，這會有點兒不切實際。

另一方面，中位數對于異常值比平均數更穩健，因為如果存在一些非常高的異常值，則平均值將被拉向某一個方向。

平均數和中位數可以用簡單的numpy單行計算：

• numpy.mean(array)
• numpy.median(array)

二、擴散(Spread)

在統計學之下，數據的擴散是指指數據被壓縮到一個或多個值的程度，這些值分布在更大的范圍內。

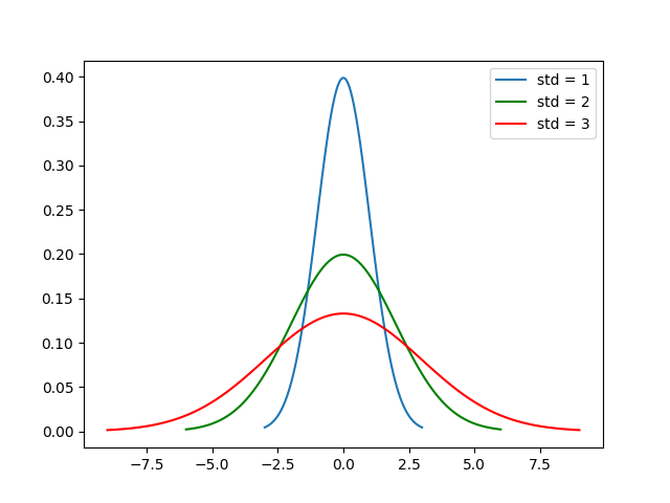
參考下面的高斯概率分布圖——假設這些是描述真實世界數據集的概率分布。

藍色曲線的擴散值最小，因為它的大部分數據點都在一個相當窄的范圍內。紅色曲線的擴散值***，因為大多數數據點所占的范圍要大得多。

圖例還顯示了這些曲線的標準偏差，這將在下一節中介紹。

標準偏差(Standard Deviation)

標準偏差是定量數據擴散程度的最常見的方式。計算標準偏差需要5個步驟：

1. 找到平均數。
2. 對于每個數據點，求其與平均值間的距離的平方。
3. 對步驟2中的值求和。
4. 除以數據點的數量。
5. 取平方根。

值越大，意味著我們的數據從平均數“擴散出去”的程度越高。值越小意味著我們的數據越集中于平均數。

計算Numpy的標準偏差：numpy.std(array)

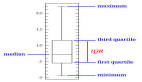
三、百分位數(Percentiles)

我們可以使用百分位數進一步描述整個范圍內每個數據點的位置。

百分位數根據數據點在值范圍中的位置高低來描述數據點的確切位置。

更正式地說，第p百分位數是數據集中的一個值，在該值處可以將數據集分為兩部分。下半部分包含p %個數據，則稱其為第p百分位數。

例如以下11個數字的集合：

• 1,3,5,7,9,11,13,15,17,19,21

數字15就是是第70百分位數，因為當我們在數字15處將數據集分成兩部分時，有70%個數據小于15。

百分位數與平均數和標準偏差相結合，可以讓我們很好地了解特定的點在數據集的擴散/范圍內的位置。如果它是一個異常值，那么它的百分位數將接近于終點——小于5%或大于95%。另一方面，如果百分位數接近50那么我們就可以知道它非常接近集中趨勢。

數組的第50個百分位數在Numpy中計算：numpy.percentile(array, 50)

四、斜度(Skewness)

數據的偏斜度衡量其不對稱性。

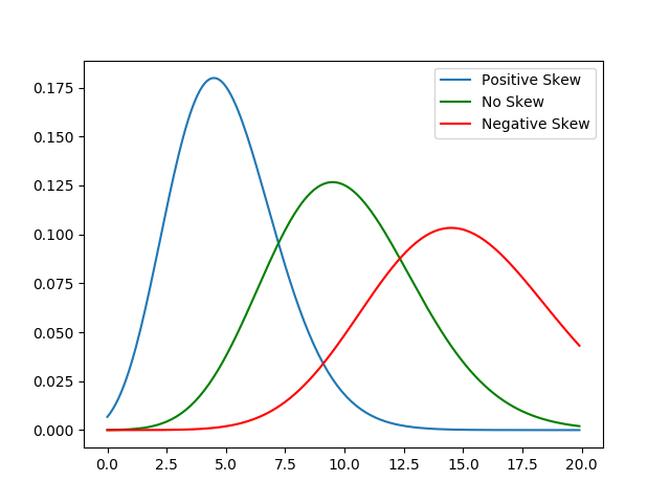
偏度為正值，表示值集中在數據點中心的左側;負偏度表示值集中在數據點中心的右側。

下圖提供了一個很好的說明。

我們可以用以下等式計算偏斜度：

偏斜度可以讓我們知道數據分布與高斯分布的距離。偏斜度越大，我們的數據集離高斯分布越遠。

這很重要，因為如果我們對數據的分布有一個粗略的概念，我們就可以為特定的分布定制我們要訓練的ML模型。此外，并非所有ML建模技術都能對非高斯數據有效。

再次提醒大家，在我們開始建模之前，統計數據能夠帶給我們非常富有洞察力的信息!

如何在Scipy代碼中計算偏斜度: scipy.stats.skew(array)

五、協方差(Covariance)和相關系數(Correlation)

協方差

兩個特征變量的協方差衡量它們之間的相關性。如果兩個變量有正協方差，那么當一個變量增加時，另一個也會增加;當協方差為負時，特征變量的值將向相反的方向變化。

相關系數

相關系數簡單來說就是標準化(縮放)的協方差，除以被分析的兩個變量的標準偏差的乘積即可得到。這有效地迫使關聯范圍始終在-1.0和1.0之間。

如果兩個特征變量的相關系數為1.0，則兩個特征變量的相關系數為正相關。這意味著，如果一個變量的變化量是給定的，那么第二個變量就會按比例向相同的方向移動。

 

用于降維的PCA圖解

 

當正相關系數小于1時，表示正相關系數小于完全正相關，且相關強度隨著數字趨近于1而增大。同樣的思想也適用于負相關值，只是特征變量的值在相反的方向變化，而不是在相同的方向變化。

了解相關性對于主成分分析(PCA)等降維技術非常有用。我們從計算一個相關矩陣開始——如果有兩個或兩個以上的變量高度相關，那么它們在解釋我們的數據時實際上是冗余的，可以刪除其中一些變量以降低復雜性。