[[283693]]

 “概率是生命的向導。”——列納德·蒙洛迪諾, 《醉漢的腳步：隨機性如何支配我們的生活》

首先，確保你想戲弄的人真的聰明。

其次，提的問題需直觀易懂。

事實上，在互聯網領域，仍存爭議的嚴謹話題所剩無幾(因為有谷歌和維基百科)。

但今天筆者要討論的是過去幾年在互聯網上引起激烈討論的話題。科學專家和數據科學家在這一問題上各有看法。

事不宜遲，現在開始吧。

[[283694]]

先來看問題

列納德·蒙洛迪諾是一名物理學家，他與斯蒂芬·霍金合著了《宏偉設計》一書。他的著作《醉漢的腳步：隨機性如何只陪我們的生活》還談到了隨機性，以及導致人們誤解隨機事件和隨機過程的認知偏見。

在介紹“樣本空間”概念的章節中，蒙洛迪諾使用了以下示例：

問題A：兒子還是女兒

我的朋友尼克有兩個孩子，他告訴你他至少有一個女兒，那么另一個孩子是女孩的概率是多少? 這似乎是一個簡單的問題，直接的回答是：已知其中一個是女孩，所以另一個孩子是女孩的幾率應該是50%，對嗎?

不對。

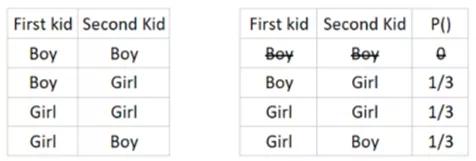
根據樣本空間理論，可以如下列出所有可能的樣本組合：

表中顯示，答案是1/3，即，33.3%。

蒙洛迪諾指出,這個問題令人困惑的部分是題目內容，如果題中指定第一個孩子為女孩，那么第二個孩子為女孩的概率是50%。

辯論

然而，另一位有識之士不同意蒙洛迪諾的理論。 加里·史密斯(Gary Smith)是波莫納學院(Pomona College)的經濟學教授。他在耶魯大學獲得經濟學博士學位，后被聘為助理教授。 他在《基本統計、回歸和計量經濟學》一書中引用了上述蒙洛迪諾采用的例子，認為這是對現實世界的典型誤解，并從另一角度提出了問題。

問題B：另一個孩子

你看到我的朋友尼克和他的女兒在街上散步。尼克告訴你他家里還有一個孩子，那么，另一個孩子是女孩的概率有多大?

這個問題看起來和蒙洛迪諾提出的問題十分相似，但加里卻給出了完全不同的答案與解析。

首先，他指出蒙洛迪諾“33.3%”的答案是錯誤的，然后他通過下表中的推算給出了自己的正確答案。

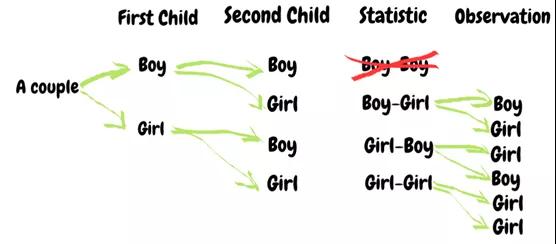
男孩用B表示，因此BB表示第一個孩子是男孩，同理，第二個孩子也是男孩。

女孩用G表示，BG表示第一個孩子是男孩，第二個是女孩。

該表顯示了400個家庭平均分配了4種孩子類型，即，每種類型為100。根據加里所證，可以得出以下推論：

已知事實

• 在100例的BB中，尼克應該總是和男孩散步。
• 在100例的GG中，尼克應該總是和女孩散步。
• 如果尼克有兒有女，則合理的假設是，他和男孩或女孩一起散步的概率是相同的。

分析

• 觀察表格的第一行。當尼克和一個女孩散步時，其中有100例(GG)表明另一位不在場的孩子也是女孩，而其他50+50例(BG&GB)則表明缺席的孩子是男孩。
• 當尼克和一個男孩散步時，也可以做出同樣的推論，因此，比較BB與BG+GB(100 vs 50+50)，也可以得出同樣的結論

結論

不管現在和尼克散步的是男孩還是女孩，另一個孩子是“男孩或女孩”概率保持不變(它們是自變量)因此答案是1/2，而不是1/3。

當然，還有一個更為直觀的解釋：你看到一個女孩，這是一個獨立的事件，對其他孩子的性別沒有影響。

如果你現在還沒有絲毫的困惑，那么你可能對這個問題還只停留在表面理解上(也可能你是個真正的天才，那便來看看下面的解釋是否與你的思維過程相同)

深入探討這個問題…

那么，加里和蒙洛迪諾，誰對誰錯?

實際上，他們都是對的，因為他們試圖解決的是兩個不同的問題。再看看以上的問題。

• A：我的朋友尼克有兩個孩子，他告訴你他至少有一個女兒，那么另一個孩子是女孩的概率是多少?
• B：你看到我的朋友尼克和他的女兒在街上散步。尼克告訴你他家里還有一個孩子，那么，另一個孩子是女孩的概率有多大?

兩個問題有什么不同嗎，“看見一個孩子是女孩”和“一個孩子是女孩”一樣嗎?

你認為呢?現在就是把聰明人弄糊涂的時候了。經濟學教授加里混淆了以上兩者的區別。

貝葉斯方程是解釋這個問題最簡單、最優雅的方法，盡管如此，筆者還是想從另一角度(使用全概率定律)來看待該問題。

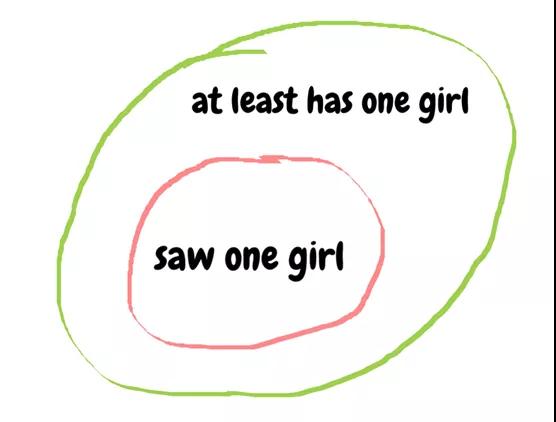
“至少有一個女兒”和“看到一個女孩”不是一回事。這是關鍵。

這兩個前提在時間和空間維度上的差異可以表示為“全局關系vs.局部關系”。

1. 空間維度上的“全球關系 VS 社會關系”

“至少有一個女兒”并不代表你能看到那個女孩

 

如上圖所示，“至少有一個女兒”包含了“看到一個女孩”，而“看到一個女孩”所傳遞的信息更具概率描述。

2. 時間維度上的“全球關系 VS 本地關系”

“至少有一個女兒”是鳥瞰的統計結果角度。

“看見一個女孩”是人類觀察的角度。

下面是更直觀的描述，

統計是對樣本空間的總體描述。觀察是對平行空間中一種可能組合(所有可能發生的事情)的實際描述。 在理解了這兩個問題之間的根本區別之后，可以得出結論：

• “至少有一個女兒”是樣本空間中的一個概率問題。因此答案是1/3;
• “看見一個女孩”是根據目前的觀察作出的未知推斷，這是一個貝葉斯統計計算。

因此，“看到一個女孩，問另一個孩子是女孩的概率”就等于“有兩個孩子，你看到其中一個是女孩，那么這個家庭有兩個女兒的概率是多少?” “猜性別”的話題到此結束。 筆者想總結的是，即使是系統1(快速直觀的本能，以及由‘或快或慢思考’產生的情感大腦)也沒有很好的概率直覺。但是，我們總是可以通過增強對概率因果關系的認識，來提高自己解釋周圍環境中的動態和不確定性的能力。

總結

如何通過概率建立主觀假設與客觀結果之間的聯系?

為什么對真實世界的觀察會影響事件的偶然性概率? 將要發生的事情和已經發生的事情有什么根本的區別?

最后，如想找到一種回答這些問題的方法，或者想戲弄你的智能數據科學家朋友，可閱讀以下書籍：

• The Drunkard’s Walk: How Randomness Rules Our Lives
• EssentialStatistics, Regression, and Econometrics
• The Book of Why: The New Science of Cause and Effect