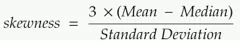數據科學實際上可定義為從數據中獲取額外信息的過程。在進行數據科學研究時，真正想要達到的是一切數據在現實世界中的實際含義。

為提取復雜數據集中的信息，數據科學家采用了許多工具和技術，包括數據探索、可視化和建模。數據探索中，常用的一類非常重要的數學技術是統計學。

實際上，統計學可對數據概要進行具體而精確地定義。使用統計學，可以描述信息的部分屬性，而非嘗試描述每個數據點。因此統計學通常足以讓人們獲得有關數據結構和構成的某些信息。

有時，人們聽到“統計”這個詞時，往往會想得過于復雜。的確，這個詞可能有點抽象，但并不總是需要通過復雜理論，才能從統計技術中獲得某種價值。

統計學中最基本的部分通常是數據科學中最實用的部分。

今天，本文將概述5種有助于數據科學研究的統計學概念。這些概念沒有那么抽象、令人抓狂，而是相當簡單、適用的技術，作用頗大。

1. 集中趨勢

[[270091]]

數據集或特征變量的集中趨勢是集的中心或典型值。我們的想法是，可能存在一單一值可(在某種程度上)***描述數據集。

例如，假設正態分布位于(100,100)的x-y位置。然后點(100,100)是集中趨勢，因為在所有可供選擇的點中，它是對數據進行概要的***點。

數據科學中可以用集中趨勢方式，快速簡單地了解數據集的整體情況。數據的“中心”可能是非常有價值的信息，告知數據集的確切偏差，因為在本質上，數據圍繞的任何值都是偏差。以數學方式選擇集中趨勢有兩種常用方法。

(1) 平均值

數據集的Mean值就是平均值，即整個數據圍繞其展開的數字。在定義Mean時，用于計算平均值的所有值均需進行等量加權。

例如，計算以下5個數字的Mean值：

(3+ 64 + 187 + 12 + 52) / 5 = 63.6 

平均值非常適合計算實際數學平均值，也適用于像Numpy這樣的Python庫，計算速度非常快

(2) 中位數

中位數是數據集的中間值，即如果將數據從最小到***(或從***到最小)排序，然后取值該集中間的值：即中位數。

再次計算和上一組相同的5個數字的中位數：

[3, 12, 52, 64, 187] → 52 

中位數與平均值63.6完全不同。不能說兩個數值孰對孰錯，但人們可以根據自身情況和目標選擇其一。

計算中位數需要對數據進行排序——如果數據集很大，那么這一做法就會變得不切實際。

此外，當異常值出現時，相較于平均值而言，中位數的數值更加穩定。因為如果出現一些非常極端的異常值，那么平均值將會變大或變小。

通過簡單的numpy單行，可計算平均值和中位數

numpy.mean(array) 
numpy.median(array) 

2. 擴散

在統計學領域，數據傳播是指數據被壓縮為單一值或分布到更為廣泛范圍的程度。

查看下方的高斯概率分布圖——假設這些圖是描述現實世界中數據集的概率分布。

藍色曲線的擴散值最小，因為其大多數數據點占據的范圍相當窄。紅色曲線的擴散值***，因為其大多數數據點占據的范圍更廣。

圖例顯示了這些曲線的標準偏差值，將在下一節中介紹。

(1) 標準偏差

標準偏差是量化數據傳播最常用的方式。計算標準偏差包括5個步驟：

• 找出平均值。
• 對于每個數據點，計算其與平均值的差值的平方值。
• 將第2步得到的值相加。
• 除以數據點的數量。
• 取平方根。

較大值意味著數據從平均值更廣泛地“展開”。較小值意味著數據越集中于平均值。

輕松計算Numpy的標準偏差：

numpy.std(array) 

3. 百分位數

使用百分位數進一步描述整個范圍內每個數據點的位置。

就某數據點在數值范圍內的高低位置而言，百分位數描述了該數據點的確切位置。

更正式地說，第p個百分位數是可分成兩部分的數據集中的值。位置較低的部分包含數據的p%，即第p個百分位數。

例如，思考以下11個數字的集合：

1, 3, 5, 7, 9, 11,13, 15, 17, 19, 21 

數字15是第70個百分位數，因為將數據集從數字15處，分成2個部分時，剩余數據中有70%的數據小于15。

百分位數與平均值和標準偏差相結合，有助于更好地了解特定數據點在數據擴散/范圍內的位置。如果該數據點為異常值，那么其百分位數將接近終值——小于5%或大于95%。另一方面，如果百分位數的計算結果接近50，那么該數據點就接近于集中趨勢。

數組的第50個百分位數可在Numpy中計算，如下所示：

numpy.percentile(array,50) 

4. 偏度

數據偏度是統計數據分布非對稱程度的數字特征。

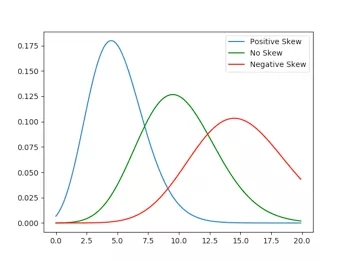
正偏意味著數值集中在數據點中心的左側; 負偏意味著數值集中在數據點中心的右側。

下圖提供了一個很好的例證。

通過以下等式可計算偏度：

偏度計算了數據分布與高斯分布的距離。偏度值越大，高斯分布離數據集就越遠。

這一點很重要，因為如果對數據分布有大概的了解，那么就可以為特定分布調整需要使用的任何ML模型。此外，并非所有ML建模技術都對高斯之外的數據有效。

進入建模前，統計學再次為人們提供了富有洞見的信息!

通過Scipy編程，計算偏度的方式如下：

scipy.stats.skew(array) 

5. 協方差和相關性

(1) 協方差

兩個特征變量的協方差用于衡量兩個變量如何“相關”。如果兩個變量為協方差的正相關，那么當一個變量增加時，另一個變量也會增加;而在若為協方差的負相關，那么兩個特征變量的值將在朝著相反方向改變。

(2) 相關性

相關性只是標準化的(縮放)協方差，除以需要分析的兩個變量的標準偏差的乘積。這可使相關范圍始終在-1.0和1.0之間。

如果兩個特征變量的相關性為1.0，則變量具有***的正相關性。這意味著如果由于給定量，一個變量發生改變，則另一變量會按照相同方向成比例地移動。

用于降維的PCA例證

正相關系數小于1表示不完全正相關，相關系數越接近1，相關性越強。這同樣適用于負相關系數，只是特征變量的值在相反方向上變化，而非在相同方向上發生變化。

了解相關性對降維所擁的主成分分析(PCA)等技術非常有必要。人們首先計算一個相關矩陣——如果有兩個或多個高度相關的變量，那么解釋數據時，變量實際上是多余的，可刪除其中一部分以降低復雜性。