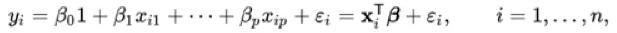實際上，數據科學家80%到90%的工作是數據清理，而這項工作的目的是為了執行其余10%的機器學習任務。沒有什么比完成數據集分析后的收獲更讓人興奮的了。如何減少清理數據的時間?如何為至關重要的10%的工作保留精力?

根據很多專業人士的經驗，對數據清理涉及的過程有充分的認知總是好的。了解流程、流程的重要性以及流程中可使用的技巧，將減少執行數據清理任務所需的時間。

[[273918]]

良好數據的重要性

好的數據被定義為準確、完整、符合、一致、及時、獨特且有效的數據。機器學習算法依賴于“好數據”來構建模型，執行和概括性能。對于實際數據，當意識到ML算法不起作用或者ML算法的性能無法在更大的數據集中推廣時，通常會發現數據問題。

在第一次數據科學的過程中找到所有數據問題幾乎是不可能的。需要做好以下準備：數據清理的迭代過程 - >數據建模 - >性能調整。在迭代過程中，通過從一開始就獲得基本面，可以大幅縮短時間。

在統計學中，經常會發現有人將數據分析過程比作約會。在最初的約會中，了解伴侶(即數據)至關重要。是否有可能在后期出現的交易破壞者?這些交易破壞者是你一開始就要抓住的，它們將使數據有失偏頗。

數據中最大的交易破壞者之一是“數據缺失”。

了解缺失的數據

缺失的數據可以有各種形狀和大小。它們可能類似于下面第1行的數據，其中只有胰島素欄有所缺失。它們也可以是第2行中丟失的許多欄數據。它們還可以是第3行中包含0的許多欄數據。需要知道它們有許多變體。可視化每列數據只能到此為止。在箱線圖中可視化每欄數據以查找異常值。或者使用熱圖來可視化數據，突出顯示缺失的數據。

吳軍的糖尿病缺失數據

在Python中：

import seaborn as sb 
sb.heatmap(df.isnull(),cbar=False) 

如何對缺失數據進行分類?

[[273919]]

在可視化缺失數據后，第一件事是對丟失的數據進行分類。

有三類缺失數據：完全缺失隨機(MCAR)，缺失隨機(MAR)，缺失不隨機(MNAR)：

MCAR—缺失值完全隨機丟失。數據點丟失的傾向與其假設值和其他變量的值無關。

MAR—由于某些觀察到的數據而缺少缺失值。數據點丟失的傾向與丟失的數據無關，但它與一些觀察到的數據有關。

MNAR—缺失的值不是隨機丟失的，而是有原因的。通常，原因在于缺失值取決于假設值，或者取決于另一個變量的值。

缺失的數據是隨機的嗎?

如果數據隨機丟失，則將以不同于隨機丟失的數據的方式來處理數據。使用Little’sMCAR測試來確定數據是否隨機丟失。

Little’sMCAR的原假設：數據完全隨機缺失。根據測試結果，你可以拒絕或接受此原假設。

在SPSS中：使用Analyze - > Missing Value Analysis - > EM

在R中，使用BaylorEdPsych集合中的LittleMCAR()函數。

傳送門：https://rdrr.io/cran/BaylorEdPsych/man/LittleMCAR.html?source=post_page

LittleMCAR(df)#df是不超過50個變量的數據幀

解釋：如果sig或統計顯著性大于0.05，則沒有統計學意義。這意味著要接受“數據完全隨機缺失”的原假設。

如果是MAR和MCAR，則刪除。

反之，估算。

刪除方法

列表刪除—此方法是指移除包含一個或多個缺失數據的整個數據記錄。

缺點—統計能力依賴于高樣本量。在較小的數據集中，列表刪除可以減少樣本量。除非確定該記錄絕對不是MNAR，否則此方法可能會給數據集引入偏差。

在Python中：

nMat <-cov（diabetes_data，use =“complete.obs”） 

成對刪除—在分析基礎上，利用變量對之間的相關性來最大化可用數據的方法。

在Python中：

nMat <-cov（diabetes_data，use =“pairwise.complete.obs”） 

缺點—由于不同數量的觀察結果對模型的不同部分有貢獻，難以解釋模型的各個部分。

刪除變量—這一方法是指，在數據缺少60%的情況下刪除變量。

diabetes_data.drop（'column_name'，axis = 1，inplace = True） 

缺點—難以知曉丟棄的變量如何影響數據集中的其他變量。

如果不能刪除，那么估算則是另一種方法。

缺失數據插補的方法

分類變量—這些變量具有固定數量的可能值。這些變量組成的一個例子是性別=男性，女性，不適用。

對于分類變量，有 3種方法來估算數據。

• 從缺失值中創建新級別
• 使用邏輯回歸、KNN等預測模型來估計數據
• 使用多個插補

連續變量—這些變量具有位于某個區間的實際值。其中的一個例子是支付金額= 0到無窮大。

對于連續變量，可以使用3種方法來估算數據。

• 使用均值、中位數、模式
• 使用線性回歸，KNN等預測模型來估算數據
• 使用多個插補

從缺失的值中創建新的級別

如果沒有大量缺失值，那么為缺失值創建新級別的分類變量是處理缺失值的好方法。

在Python中：

import pandas as pd 
  
diabetes=pd.read_csv('data/diabetes.csv') 
diabetes["Gender"].fillna("No Gender", inplace=diabetes 

平均值、中位數、模式

該方法涉及使用平均值，中位數或模式來估算缺失的數據。這種方法的優點是它很容易實現。但同時也有許多缺點。

在Python中：

df.Column_Name.fillna（df.Column_Name.mean（），inplace = True） 
df.Column_Name.fillna（df.Column_Name.median（），inplace = True） 
df.Column_Name.fillna（df.Column_Name.mode（），inplace = True） 

平均值、中位數、模式估算的缺點—它減少了估算變量的方差，也縮小了標準誤差，這使大多數假設檢驗和置信區間的計算無效。它忽略了變量之間的相關性，可能過度表示和低估某些數據。

邏輯回歸

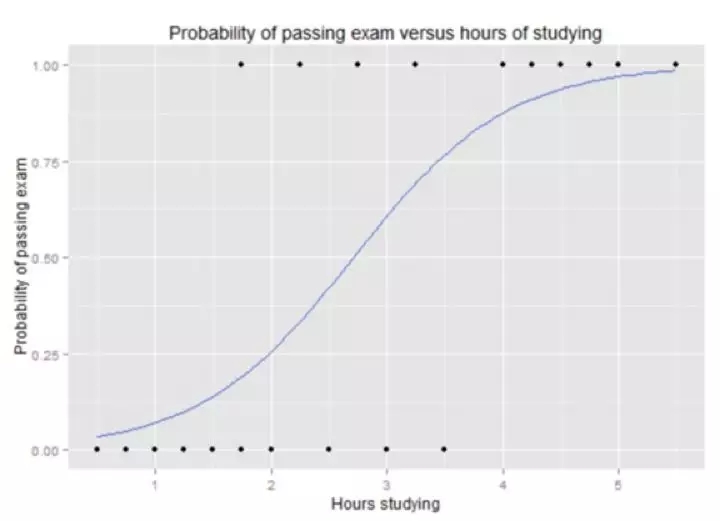
以一個統計模型為例，它使用邏輯函數來建模因變量。因變量是二進制因變量，其中兩個值標記為“0”和“1”。邏輯函數是一個S函數，其中輸入是對數幾率，輸出是概率。(例如：Y：通過考試的概率，X：學習時間.S函數的圖形如下圖)

圖片來自維基百科：邏輯回歸

在Python中：

from sklearn.pipeline import Pipeline 
from sklearn.preprocessing import Imputer 
from sklearn.linear_model import LogisticRegression 
 
imp=Imputer(missing_values="NaN", strategy="mean", axis=0) 
logmodel = LogisticRegression() 
steps=[('imputation',imp),('logistic_regression',logmodel)] 
pipeline=Pipeline(steps) 
X_train, X_test, Y_train, Y_test=train_test_split(X, y, test_size=0.3,random_state=42) 
pipeline.fit(X_train, Y_train) 
y_pred=pipeline.predict(X_test) 
pipeline.score(X_test, Y_test) 

邏輯回歸的缺點：

• 由于夸大其預測準確性的事實，容易過度自信或過度擬合。
• 當存在多個或非線性決策邊界時，往往表現不佳。
• 線性回歸

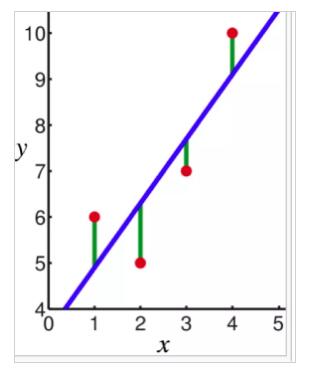
以一個統計模型為例，它使用線性預測函數來模擬因變量。因變量y和自變量x之間的關系是線性的。在這種情況下，系數是線的斜率。點到線形成的距離標記為(綠色)是誤差項。

圖片來自維基百科：線性回歸

圖片來自維基百科：線性回歸

在Python中：

from sklearn.linear_model import LinearModel 
from sklearn.preprocessing import Imputer 
from sklearn.pipeline import Pipeline 
 
imp=Imputer(missing_values="NaN", strategy="mean", axis=0) 
linmodel = LinearModel() 
steps=[('imputation',imp),('linear_regression',linmodel)] 
pipeline=Pipeline(steps) 
X_train, X_test, Y_train, Y_test=train_test_split(X, y, test_size=0.3,random_state=42) 
pipeline.fit(X_train, Y_train) 
y_pred=pipeline.predict(X_test) 
pipeline.score(X_test, Y_test 

線性回歸的缺點：

• 標準錯誤縮小
• x和y之間需具有線性關系

KNN(K-近鄰算法)

這是一種廣泛用于缺失數據插補的模型。它被廣泛使用的原因是它可以處理連續數據和分類數據。

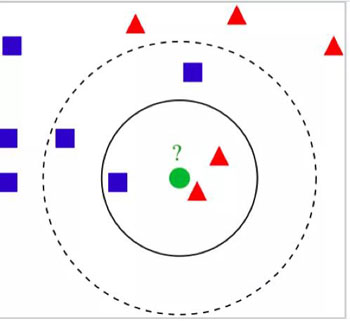
此模型是一種非參數方法，可將數據分類到最近的重度加權鄰居。用于連續變量的距離是歐幾里德，對于分類數據，它可以是漢明距離(Hamming Distance)。在下面的例子中，綠色圓圈是Y。它和紅色三角形劃分到一起而不是藍色方塊，因為它附近有兩個紅色三角形。

圖片來自維基百科：KNN

from sklearn.neighbors import KNeighborsClassifier 
from sklearn.preprocessing import Imputer 
from sklearn.pipeline import Pipeline 
 
k_range=range(1,26) 
  
for k in k_range: 
 imp=Imputer(missing_values=”NaN”,strategy=”mean”, axis=0) 
 knn=KNeighborsClassifier(n_neighbors=k) 
 steps=[(‘imputation’,imp),(‘K-NearestNeighbor’,knn)] 
 pipeline=Pipeline(steps) 
 X_train, X_test, Y_train,Y_test=train_test_split(X, y, test_size=0.3, random_state=42) 
 pipeline.fit(X_train, Y_train) 
 y_pred=pipeline.predict(X_test) 
 pipeline.score(X_test, Y_test) 

KNN的缺點：

• 在較大的數據集上耗費時間長
• 在高維數據上，精度可能會嚴重降低

多重插補

多個插補或MICE算法通過運行多個回歸模型來工作，并且每個缺失值均根據觀察到(非缺失)的值有條件地建模。多次估算的強大之處在于它可估算連續，二進制，無序分類和有序分類數據的混合。

多重插補的步驟是：

• 用鼠標輸入數據()
• 使用with()構建模型
• 使用pool()匯集所有模型的結果

在R中，MICE集提供多個插補。

library(mice) 
imp<-mice(diabetes, method="norm.predict", m=1) 
data_imp<-complete(imp) 
imp<-mice(diabetes, m=5) 
fit<-with(data=imp, lm(y~x+z)) 
combine<-pool(fit) 

MICE的缺點：

• 不像其他估算方法一樣具有理論依據
• 數據的復雜性

處理缺失的數據是數據科學家工作的最重要部分之一。算法中擁有干凈的數據意味著你的機器學習算法的性能會更好。在數據清理過程開始時，區分MCAR，MAR，MNAR是必不可少的。雖然有不同的方法來處理缺失的數據插補，但KNN和MICE仍然是處理連續和分類數據的最受歡迎的方法。