一個退休程序員,用高中幾何方法,讓百年數學難題逼近理論極限
本文經AI新媒體量子位(公眾號ID:QbitAI)授權轉載,轉載請聯系出處。
試想一下,如果你的褲子破了好幾個洞,每個洞形狀各異,但是寬度都不超過1厘米。
該如何設計一個通用的補丁,能夠把所有的洞都補上呢?
這個問題在數學上叫做:萬有覆蓋問題(universal covering problem)。
已經讓數學家思考了一百年。
乍一聽上去,這像是一個很簡單的問題。
但是稍微想一想,似乎又不那么簡單。
比如一個邊長為1的等腰三角形,和一個直徑為1 的圓形,兩者的直徑都為 1。
但是,這個三角形就不能被圓形覆蓋。
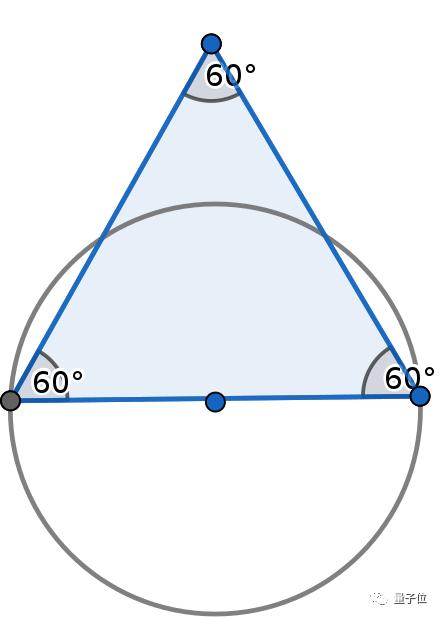
而最近,一個退休程序員,用高中方法取得了最新進展。
為什么這么難?
這個難題的的提出者,法國著名數學家:勒貝格(Henri Léon Lebesgue)。
△Henri Léon Lebesgue
他提出了勒貝格積分,拓寬了積分學的研究范圍。
在1914時,他給好朋友Julius Pál(也是數學家)寫信時提了一個問題:
在一個平面上,找一個最小區域,讓它可以覆蓋直徑不超過1個單位的面積?
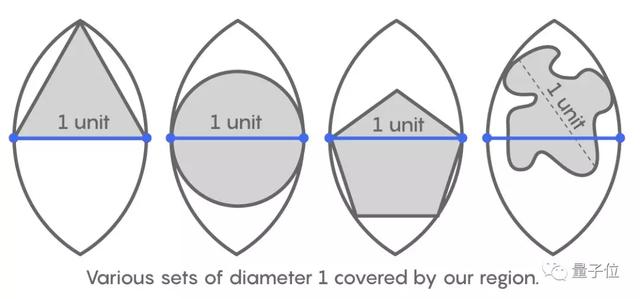
直徑不超過1個單位的任意形狀,就是一個封閉曲線的邊緣上,最遠兩點的距離不超過1個單位。
這個問題最難的部分是:
無法窮舉所有直徑為1的形狀到底長什么樣子。
直徑為1的形狀千千萬,到底用哪種萬能補丁才能全部覆蓋它們呢?
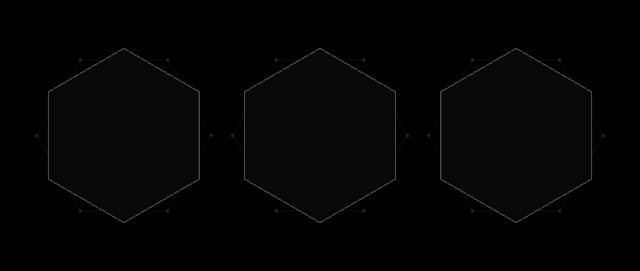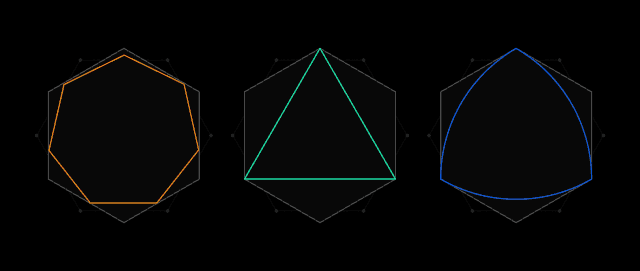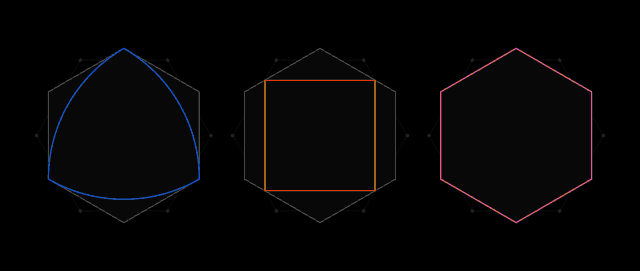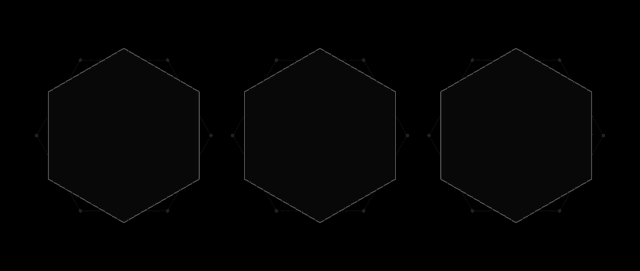
萬有覆蓋“通用”方法
但是這個問題并不難上手,只要你有高中數學基礎,就可以試一下。
接下來,讓我們一起看看數學家們目前解決這個問題的方法。
從直徑為1的需要覆蓋的區域R入手。
雖然不知道R長什么樣子,能夠確定的一點是:它絕對不會超過1個單位的寬度。
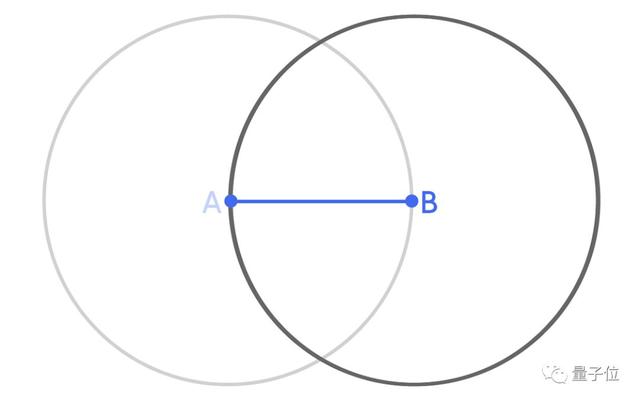
那么就先假設它有2個點——A和B,距離為1個單位。

現在,我們假設除了A和B之外,在R區域內還存在一個點C。
那么C可能在哪里呢?
它不可能大于A的1個單位,這意味著它必須在以A為圓心且半徑為1的圓中。
但另外一個問題是,C和B的距離也不能超過1個單位。
所以C也必須在以B為圓心且半徑為1的圓中。
所以,C的位置就確定在了兩個圓形的交集位置。
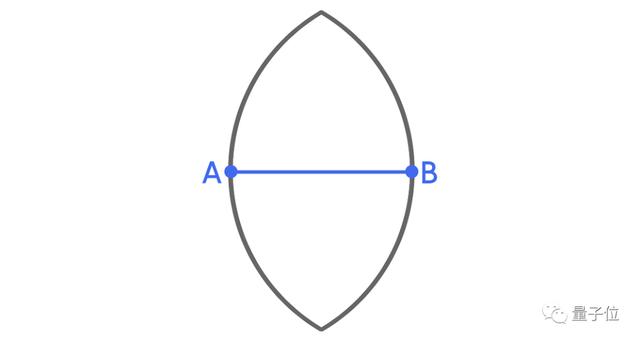
到A和B的距離不能超過1,這一條件不僅僅適用于點C,還適用于區域R中的每個點。
所以R中的每一個點都必須位于這兩個圓的交集區域中。
換句話說,這個區域可以覆蓋直徑為1的所有可能的R集,是一個萬有覆蓋區域。
但是這個區域不是最小面積,需要對它進行一下修剪。
注意,圓的相交點形成兩個等邊三角形,頂點分別是是A、B,以及距離AB中點垂直距離為√3/2的上下兩個點。
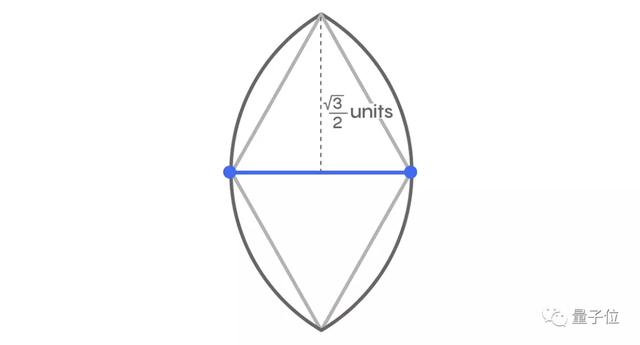
因為√3/2大于1/2,我們可以畫兩條平行線,與AB平行,距離AB 1/2個單位。
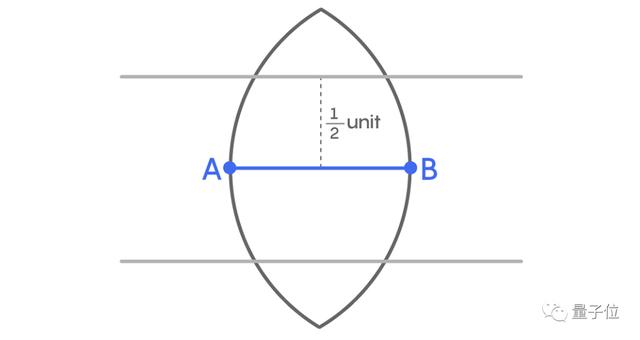
現在,考慮下圖中紅色的區域。
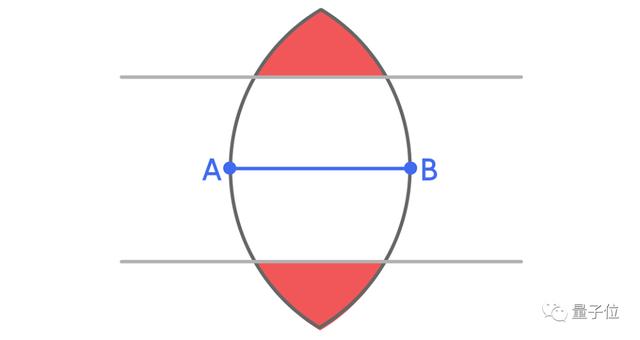
因為兩個平行線之間的距離為1個單位,所以直徑為1的集合不可能同時出現在兩個紅色區域。就可以去掉一個。
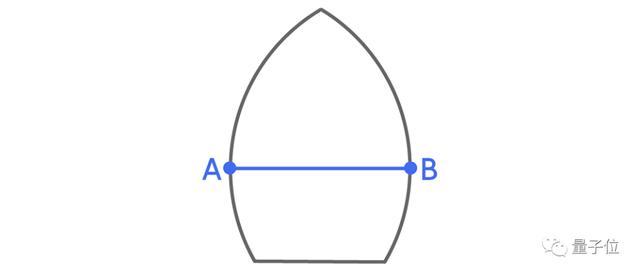
這樣萬有覆蓋面積從原來的(2π/3)-(√3/2)≈1.228,減少到(π/2)-1/2≈1.071
從一個基本的萬有覆蓋開始,可以通過去掉一個無關緊要的部分,來縮小它的面積。
這就是數學家們得到最小萬有覆蓋的方法。
優化方法:Pál六邊形
通過更先進的技術,我們還能找到一些其他的簡單形狀。
Pál利用定寬曲線的特性表明:
即使直徑為1的一組曲線,可能會從直徑1的圓中“伸”出來,它也總是可以通過移動或旋轉,以適應圍成這個圓的六邊形。
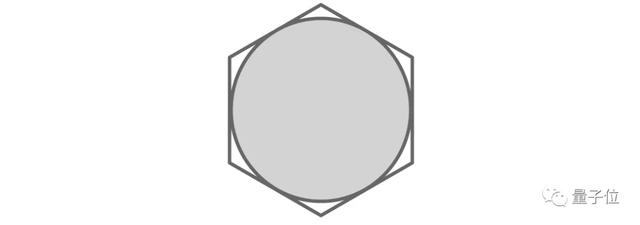
下圖就展示了Pál提出的,可以覆蓋各種形狀(直徑為1)的六邊形。
上圖中間的形狀是一個勒洛三角形(Reuleaux triangle),這是一個與我們上一小節提到的萬有覆蓋密切相關的定寬曲線。
勒洛三角形是一個弧三角形,通過三個相同的圓可以獲得。
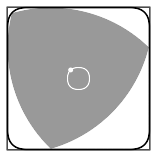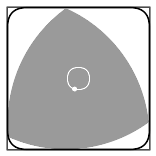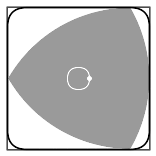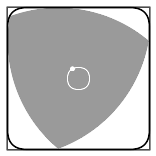
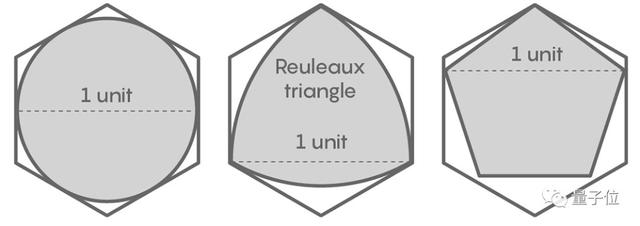
這個六邊形的面積是√3/2≈0.866,比我們上小節所得到的面積還要小。
但Pál也表示,并不需要整個六邊形。
他通過巧妙的旋轉,去掉了一些無關部分。
首先,將兩個Pál六邊形堆疊在一起。
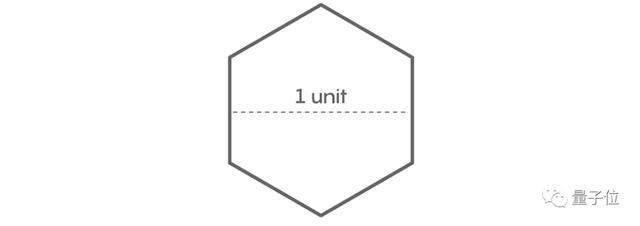
其中一個六邊形繞中心旋轉30度。
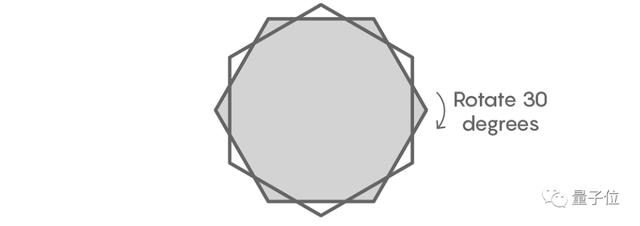
出現了6個紅色小三角形。
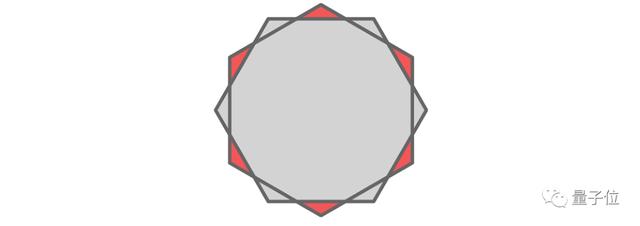
每個紅色小三角形,都處在未旋轉六邊形的外部,以及旋轉六邊形的內部。
由于每個六邊形平行對邊的距離是1個單位,所以對著的兩個紅色小三角形中的點距離肯定大于1個單位。
也就是說,一組直徑為1的形狀不可能同時出現在兩個相對的紅色小三角形中。
按照上一小節的思路,可能會覺得應該能從6個小三角形去掉3個小三角形,但實際上是不行的。
因為一個六邊形旋轉60度,或者對稱翻轉一下,都不會發生形狀的改變。
所以從相對的一對中選擇一個紅色三角形只有兩種不同的方法:
3個三角形可以是連續的,也可以是交替的。
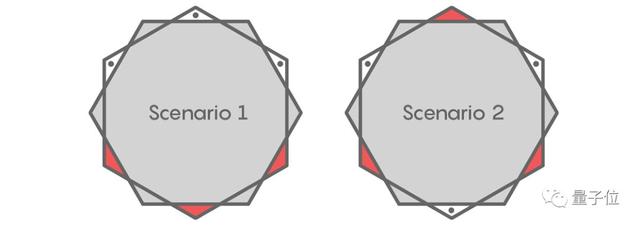
但是,我們可以去掉2個這樣的小三角形。Pál就是這么做的。
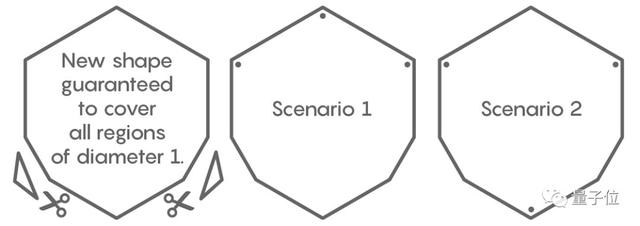
他從他的六邊形上切下兩個三角形,得到一個保證能覆蓋所有直徑為1的區域的新形狀。
這種新的萬有覆蓋的面積是2-2/√3≈0.8453,比六邊形面積略小一些。
但是Pál六邊形并不是最優解。
在此基礎上,數學家和數學愛好者們繼續修修剪剪。
在1992年,數學家Roland Sprague和HC Hansen在Pál六邊形上減去了三個小細條。
使面積縮小為0.844137708416。
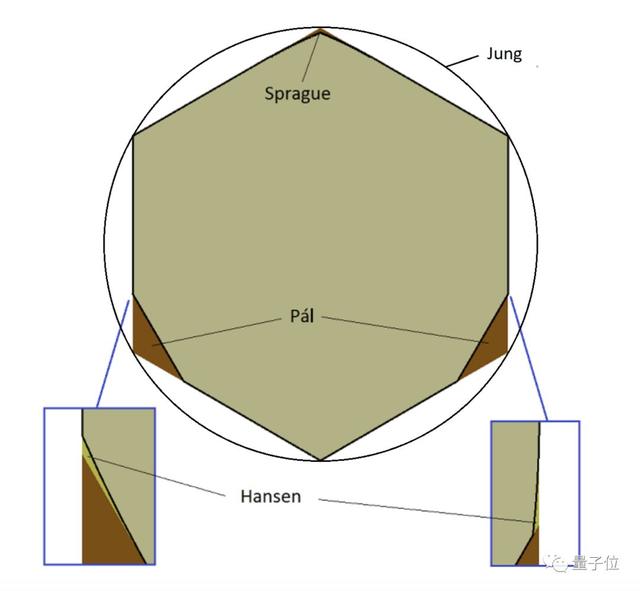
Sprague減少了0.001單位面積,Hansen減少了0.00000000004單位面積。
退休程序員用高中幾何,兩次逼近極限
然后二十年過去了,這個問題毫無進展。
直到2014年,一位叫做Philip Gibbs的退休軟件工程師嘗試解決這個數學問題。
他利用自己的編程背景優勢,嘗試用電腦解來解決。
△Philip Gibbs
Gibbs首先對200個隨機生成的直徑為1的形狀進行了計算機模擬。
這些模擬結果表明,他或許能夠修剪一個最小萬有覆蓋空間頂部角落的一些區域。
隨后,他證明了新的覆蓋對所有可能的直徑為1的形狀都適用。
2015年2月,Gibbs和兩位共同研究者將論文發表在了網上。

△論文地址:https://arxiv.org/abs/1502.01251
他們把最小萬有覆蓋面從0.8441377減少到0.8441153單位面積。
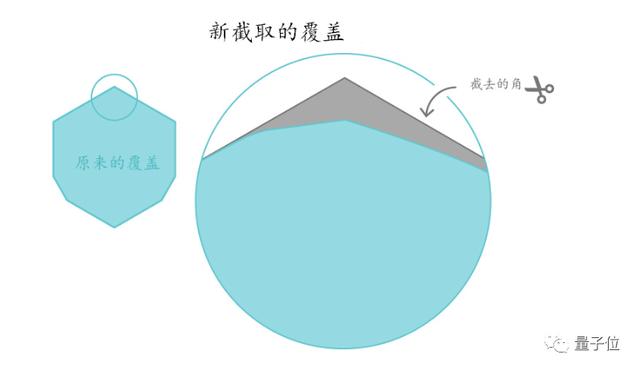
他的策略是將所有直徑為1的形狀移到他早些年發現的萬有覆蓋的某一角。
然后把對角部分剩下的任何區域都去掉;然而從節省面積測量的角度來說,卻是非常精確的。
雖然此次減小的單位面積只有0.0000224,但這卻幾乎是漢森在1992年減少的面積的100萬倍!
然而,這并未阻止他進一步的“裁剪”。
2018年10月,Gibbs獨自又發布了一篇文章,再次將最小萬有覆蓋面積縮小。

△論文地址:https://arxiv.org/abs/1810.10089
要知道,在Gibbs的基礎上再縮小覆蓋面積實屬不易。正如來自加州大學河濱分校的數學家約翰·貝茲所說:
你不可能真的把這些碎片畫出來,因為他們都是原子大小的。
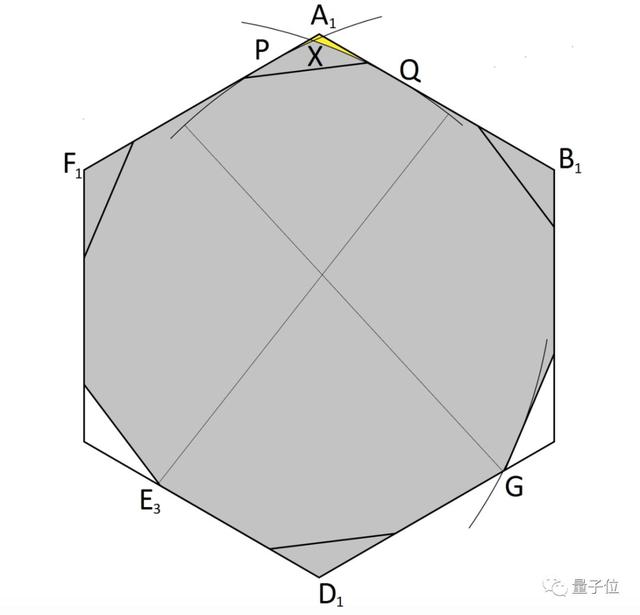
而Gibbs卻再次突破了極限,堪稱原子剪刀。
這一次他的著手點是上圖中的點A和點E。
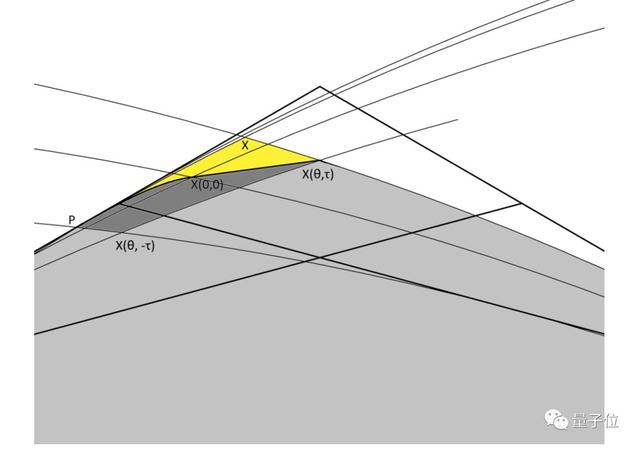
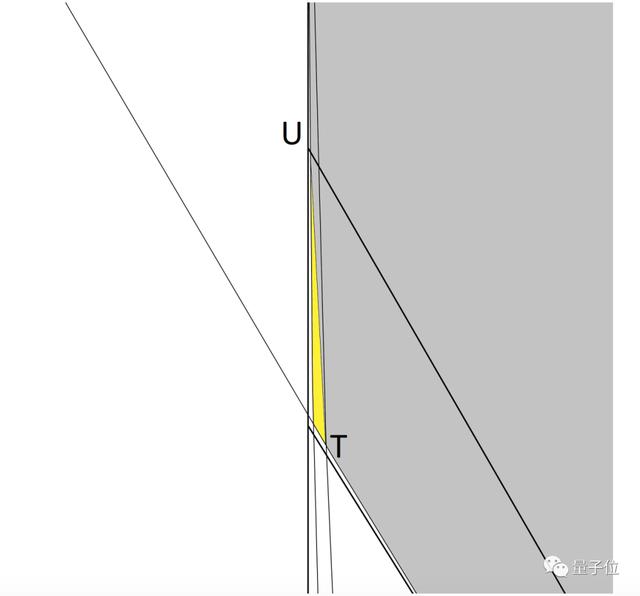
最終,通過這次研究,得到的最小面積就是0.8440935944。
值得一提的是,實驗方法基本都屬于高中幾何知識。
正如貝茲所評價:
從數學角度來說,這只是高中幾何難度,但是它幾乎讓人為之瘋狂。
極限挑戰,仍將繼續
問題雖然還沒有最終解決,但是在2005年的時候,有數學家計算出了這個問題的理論下限,萬有覆蓋范圍不能小于0.832單位面積。
抵達終點最后一步步依舊等待人來跨越,困難之處依舊在于,直徑唯一的形狀千變萬化,最后給出的范圍需要涵蓋所有可能性。
如果你做到了,名字就將載入數學史。
傳送門
QuantaMagazine博客:
https://www.quantamagazine.org/how-simple-math-can-cover-even-the-most-complex-holes-20200108/
https://www.quantamagazine.org/amateur-mathematician-finds-smallest-universal-cover-20181115/
GitHub項目地址:
https://github.com/guadaran/lebesgue-universal-covering-problem




























