[[316755]]

大數(shù)據(jù)文摘出品

來(lái)源：towardsdatascience

編譯：大萌、趙吉克、武帥、錢(qián)天培

2019年末，在中國(guó)武漢爆發(fā)的冠狀病毒疫情沖擊了整個(gè)金融市場(chǎng)和實(shí)體經(jīng)濟(jì)。這座總?cè)丝诔^(guò)千萬(wàn)，春運(yùn)期間流動(dòng)人口超過(guò)500萬(wàn)的巨型城市的災(zāi)難在世界各地引發(fā)了一連串蝴蝶效應(yīng)，也在全球普通民眾中引發(fā)恐慌。

2020年1月30日，2019-nCoV已被世界衛(wèi)生組織列為國(guó)際關(guān)注的突發(fā)公共衛(wèi)生事件(PHEIC)。在撰寫(xiě)本文時(shí)，尚未發(fā)現(xiàn)經(jīng)過(guò)醫(yī)學(xué)研究驗(yàn)證的具體治療方法。

此外，一些關(guān)鍵的流行病學(xué)指標(biāo)，如基本再生數(shù)(一個(gè)感染者傳染的平均人數(shù)，即R0值)仍然未知。當(dāng)今時(shí)代，全球互聯(lián)，這類(lèi)流行病更是借勢(shì)成為全球范圍內(nèi)的重大威脅之一。

可以推測(cè)，如果2020年全球發(fā)生災(zāi)難性事件(大致定義為導(dǎo)致不少于1億人傷亡的事件)，最有可能的原因恰恰是某種流行病——而不是核災(zāi)難，也不是氣候?yàn)?zāi)難，等等。全球范圍內(nèi)的快速城市化進(jìn)一步加劇了這一問(wèn)題，人口密集且頻繁流動(dòng)的城市儼然變成了疾病擴(kuò)散網(wǎng)絡(luò)的傳播節(jié)點(diǎn)，使得防疫系統(tǒng)變得極為脆弱。

武漢的這場(chǎng)災(zāi)難也引發(fā)了全球?qū)τ诔鞘幸?guī)劃和防疫政策的思考。如果疾病不是在武漢，而是在另一座人口規(guī)模更小、人口流動(dòng)也更弱的城市，它的傳染性和感染人數(shù)，又會(huì)是怎樣的故事?

在這篇文章中，我們將討論當(dāng)流行病襲擊一個(gè)城市時(shí)會(huì)發(fā)生什么，應(yīng)該立即采取什么措施，以及這對(duì)城市規(guī)劃、政策制定和管理有什么影響。

我們將以亞美尼亞首都，一個(gè)人口剛過(guò)百萬(wàn)、以鋼鐵和葡萄酒著名的城市埃里溫市為例進(jìn)行研究，建立數(shù)學(xué)模型并模擬冠狀病毒在該市的傳播，研究城市流動(dòng)模式如何影響疾病的傳播。

城市流動(dòng)性

有效、高效和可持續(xù)的城市流動(dòng)性對(duì)現(xiàn)代城市的運(yùn)作至關(guān)重要。它已經(jīng)被證明會(huì)直接影響城市的宜居性和經(jīng)濟(jì)產(chǎn)出(GDP)。然而，一旦發(fā)生疫情，它就會(huì)火上澆油，擴(kuò)大疾病的傳播。

那么，讓我們先來(lái)看看埃里溫市在一個(gè)平面坐標(biāo)系上的聚合OD流動(dòng)網(wǎng)絡(luò)(Origin-Destination)，以了解城市流動(dòng)模式的空間結(jié)構(gòu)：

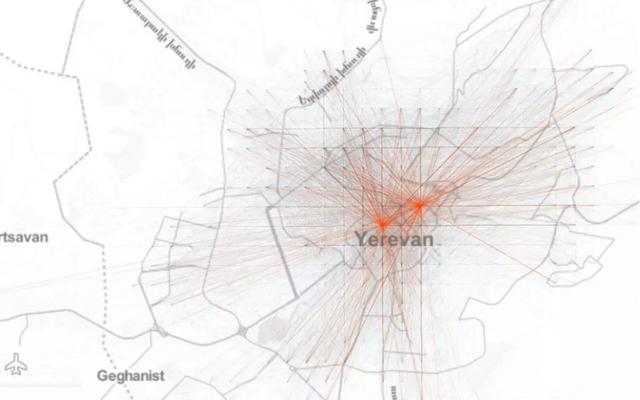
接著，如果我們觀察網(wǎng)格的總流入量，我們會(huì)看到或多或少的單中心空間組織，其中一些網(wǎng)格的日流入量較高但位于中心之外:

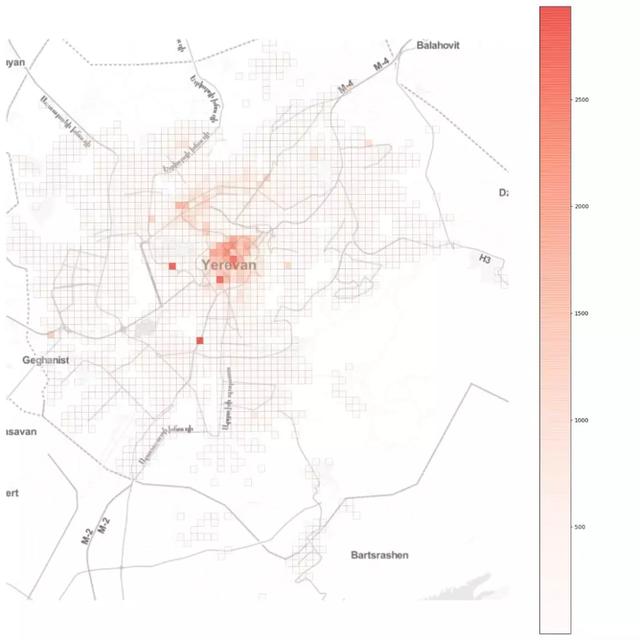
現(xiàn)在，假設(shè)一種流行病在城市的任意地點(diǎn)爆發(fā)。它將如何傳播?我們能做些什么來(lái)控制它?

流行病學(xué)建模

為了回答這些問(wèn)題，我們將建立一個(gè)簡(jiǎn)單的房室模型來(lái)模擬傳染病在城市中的傳播。

當(dāng)一種流行病爆發(fā)時(shí)，其傳播動(dòng)力會(huì)有顯著變化，這取決于最初感染的地理位置及其與城市其他地區(qū)的連接性。這是最近關(guān)于城市人口流行病的數(shù)據(jù)驅(qū)動(dòng)研究得出的最重要見(jiàn)解之一。然而，正如我們將在下文進(jìn)一步看到的，各種結(jié)果都要求采取類(lèi)似的措施來(lái)控制疫情，并在規(guī)劃和管理城市時(shí)考慮到這種可能性。

注：compartmental model，房室模型，也稱(chēng)SIR模型，是一種簡(jiǎn)化的傳染病數(shù)學(xué)模型。

由于我們的目標(biāo)是展示城市流行病傳播的一般原理，而不是建立一個(gè)實(shí)時(shí)的精確模型，我將參考《自然》雜志的一篇文章，通過(guò)簡(jiǎn)單地修改經(jīng)典SIR模型即可滿(mǎn)足我們的需求。

相關(guān)鏈接：https://www.nature.com/articles/s41467-017-02064-4

這個(gè)模型把人口分成三部分。在時(shí)間t的每個(gè)位置i，其三個(gè)房室如下：

• Si,t：尚未感染或易感的人數(shù);
• Ii,t：感染疾病并有能力將疾病傳播給易感人群的人數(shù);
• Ri,t：由于康復(fù)或者死亡，在被感染后從受感染組中移除的人數(shù)。這個(gè)群體中的個(gè)體沒(méi)有能力再次感染該疾病或?qū)⒏腥静魅窘o他人。

在我們的模擬中，時(shí)間將是一個(gè)離散變量，因?yàn)橄到y(tǒng)的狀態(tài)是以日為單位進(jìn)行建模的。在t時(shí)刻j點(diǎn)的完全易感人群中，感染病出現(xiàn)的概率為：

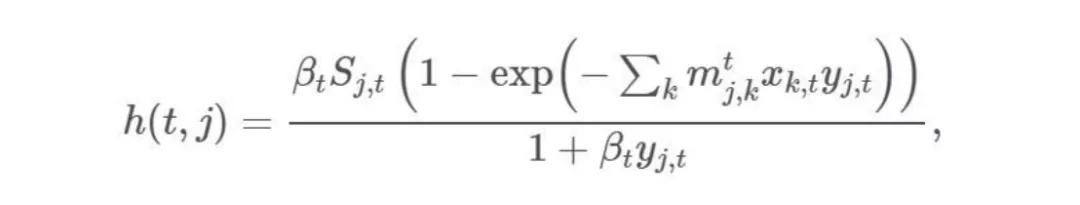
βt是t時(shí)刻的傳輸率; mj,k是從k地到j(luò)地的流動(dòng)性, xk,t 和yk,t 代表t時(shí)刻k地和j地的感染和易感人群數(shù)，其中xk,t = Ik,t / Nk，yj,t = Sj,t / Nj，Nk和Nj代表k地和j地的人口總數(shù)。然后，我們繼續(xù)模擬一個(gè)隨機(jī)過(guò)程，將這種疾病引入完全易感人群所在的地區(qū),其中Ij,t+1 是概率為h(t,j)的伯努利隨機(jī)變量。

一旦感染在隨機(jī)地點(diǎn)出現(xiàn)，疾病不僅會(huì)在該地點(diǎn)傳播，還會(huì)通過(guò)攜帶者傳播到他處。這就是以O(shè)D流矩陣為特征的城市流動(dòng)模式發(fā)揮關(guān)鍵作用的地方。

此外，為了確定疾病是如何通過(guò)感染者傳播的，我們需要考慮其R0值。此處，其中y表示的是治愈率，也可以認(rèn)為是二次感染率。在撰寫(xiě)本文時(shí)，新型冠狀病毒的基本再生數(shù)估計(jì)值在1.4到4之間。凡事做最壞的準(zhǔn)備，因此我們假設(shè)R0值為4。需要注意的是，R0值是一個(gè)有期望值的隨機(jī)變量。為了讓事情更有趣一點(diǎn)，我們?cè)诿總€(gè)地區(qū)采用不同的R0值進(jìn)行模擬，其中R0值服從均值為4的伽瑪分布：

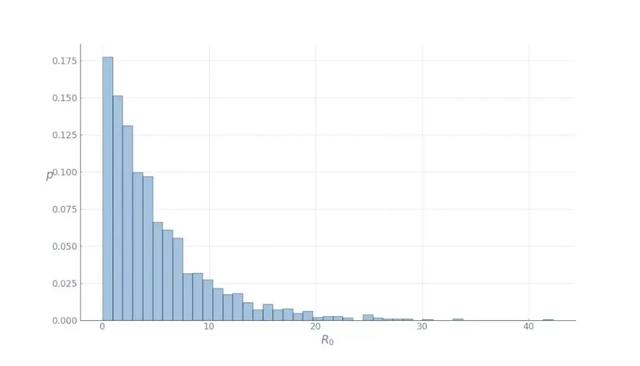
現(xiàn)在我們來(lái)討論所建立的模型：

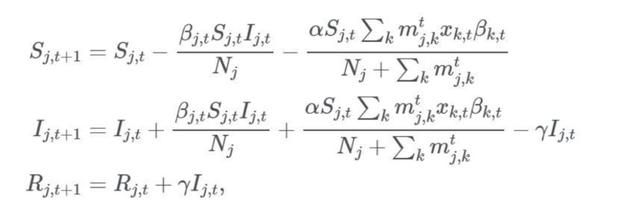
βk,t是t時(shí)刻k地的轉(zhuǎn)移率，α是刻畫(huà)出行方式傾向的參數(shù)。

上述的模型十分簡(jiǎn)潔：為了求得t + 1時(shí)刻的j地的尚未感染或易感的人數(shù)，我們需要從t時(shí)刻的j地的尚未感染或易感的人數(shù)中減去j地本地感染的人數(shù)(第一個(gè)方程的第二部分)，還要減去從其他地方來(lái)到j(luò)地的感染者數(shù)，這些外來(lái)的感染者通過(guò)其傳輸率進(jìn)行加權(quán)計(jì)算(第一個(gè)方程的第三部分)。由于總?cè)丝跀?shù)Nj = Sj + Ij + Rj，我們需要將減去的部分移至感染組，同時(shí)將治愈的部分移至Rj,t+1(第二個(gè)和第三個(gè)方程)。

仿真建立

在此分析中，我們將使用由當(dāng)?shù)毓渤斯緂g提供的GPS數(shù)據(jù)獲得的一個(gè)典型日的總OD流量矩陣作為埃里溫市交通模式的代表。

接下來(lái)，我們需要每個(gè)250×250m網(wǎng)格單元的人口計(jì)數(shù)，通過(guò)按比例縮放提取的流量計(jì)數(shù)來(lái)近似計(jì)算，從而使不同位置的總流入量之和接近埃里溫市110萬(wàn)人口的一半。這是一個(gè)大膽的假設(shè)，但對(duì)結(jié)果影響不大。

減少公共交通?

第一次模擬，我們將模擬背景設(shè)定為一個(gè)高度依賴(lài)公共交通的未來(lái)城市，設(shè)定流動(dòng)率α=0.9：

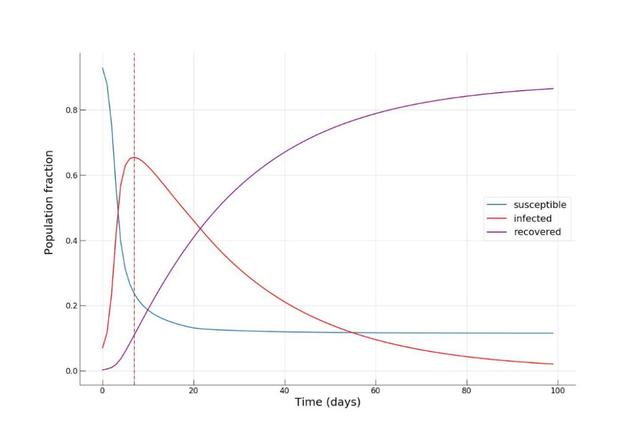
可以看到，經(jīng)過(guò)大約8-10天左右的時(shí)間感染人數(shù)比例迅速增加至70%，達(dá)到峰值，但此時(shí)僅有小部分(約10%)的人康復(fù)。至100天時(shí)，疫情逐漸緩解，康復(fù)人數(shù)比例達(dá)到了驚人的90%!現(xiàn)在，我們?cè)賮?lái)看一下如果將公共交通強(qiáng)度α降低至0.2時(shí)，是否有利于緩解傳染病的傳播。這可以解釋為采取嚴(yán)厲措施來(lái)降低城市流動(dòng)性(例如實(shí)施宵禁)，或者增加私家車(chē)出行比例，以減少人們出行期間感染的機(jī)率。

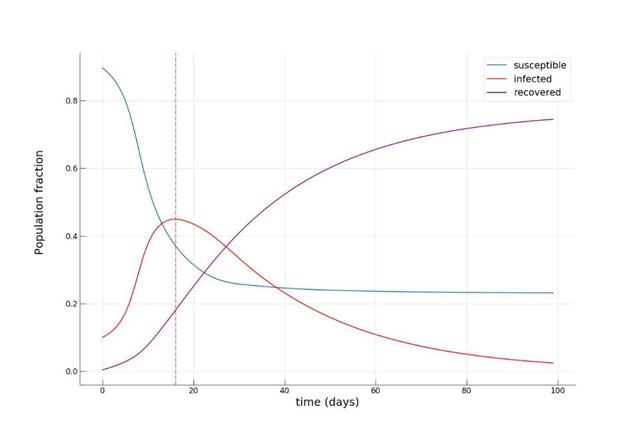
可以發(fā)現(xiàn)在這種假設(shè)下，疫情在16至20天左右到達(dá)頂峰，峰值感染人數(shù)比例明顯降低(約45%)，并且此時(shí)康復(fù)人數(shù)為之前的兩倍(約20%)。在疫情結(jié)行將結(jié)束時(shí)，易感染人群比例也是之前的兩倍(約24% vs. 約12%)，這意味著更多的人躲過(guò)了這場(chǎng)疫情。正如人們所期望的，通過(guò)實(shí)施嚴(yán)厲的管控措施來(lái)臨時(shí)降低城市的流動(dòng)性對(duì)于減少傳染病傳播有明顯作用。

隔離熱門(mén)區(qū)域?

接著，再來(lái)看另一個(gè)直觀想法——隔離一些關(guān)鍵區(qū)域能否得到預(yù)期的效果。為了測(cè)試這一想法，先挑選人流量位于前1%的區(qū)域：

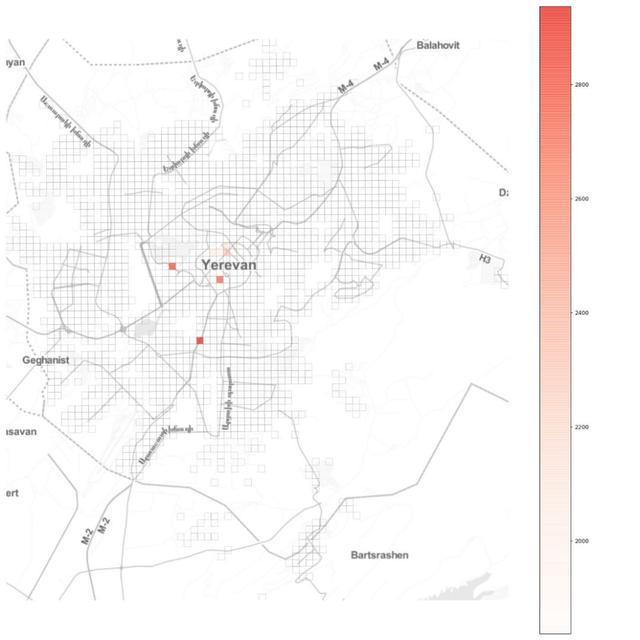
接著完全限制這些區(qū)域的進(jìn)出，建立有效的隔離制度。從這張圖我們可以看出，在埃里溫市這些位置主要位于市中心，另兩個(gè)位置是兩家最大的購(gòu)物商場(chǎng)。將α取中間值，即0.5，我們得到如下結(jié)果：

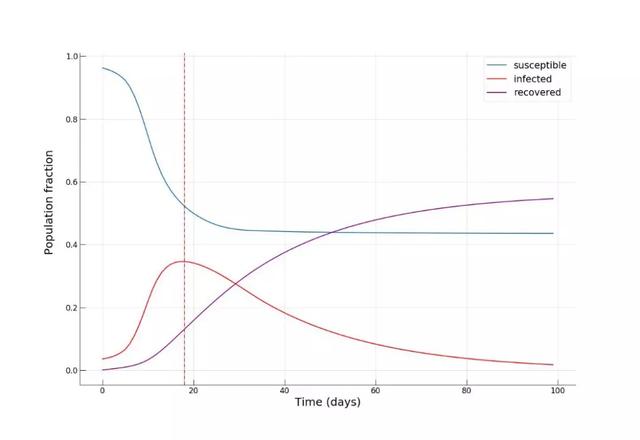
感染人數(shù)比例的峰值更小了(約35%)，并且更重要的是，在疫情行將結(jié)束時(shí)，大約一半的人未被感染，說(shuō)明該種方法能夠幫助人們有效的降低感染風(fēng)險(xiǎn)!

如下動(dòng)圖顯示了高度依賴(lài)公共交通場(chǎng)景下的結(jié)果：

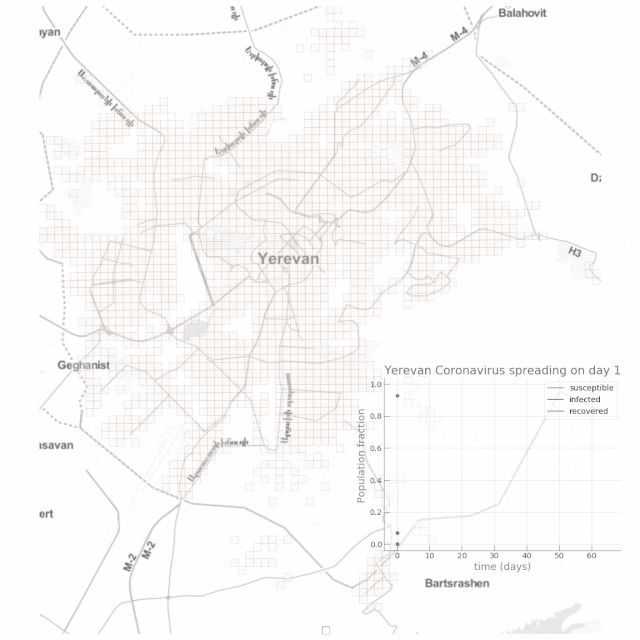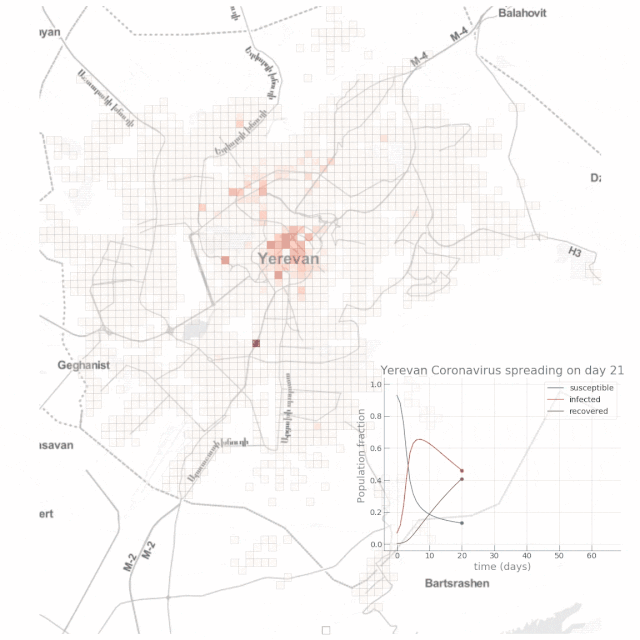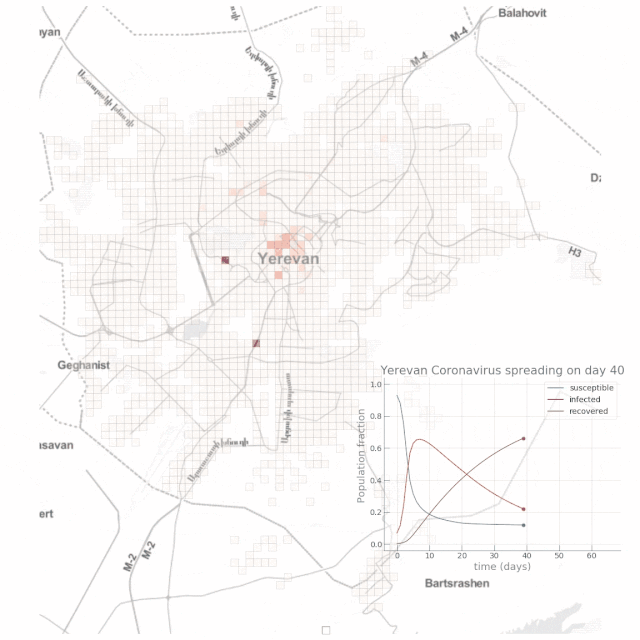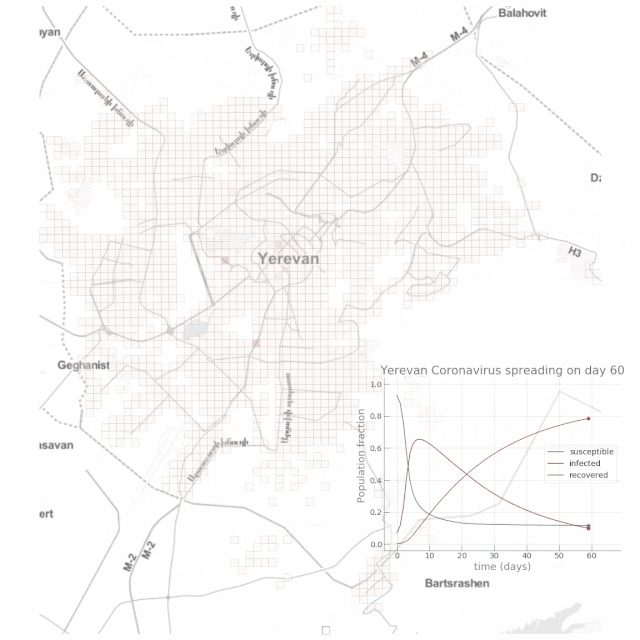
結(jié)論

該實(shí)驗(yàn)絕不是說(shuō)我們已經(jīng)構(gòu)建了準(zhǔn)確的傳染病模型(甚至模型中不涉及任何傳染病學(xué)的基礎(chǔ)知識(shí))，我們的目標(biāo)是在傳染病爆發(fā)時(shí)能夠即時(shí)了解城市交通網(wǎng)絡(luò)對(duì)傳染病傳播的影響。

隨著人口密度、流動(dòng)性和互動(dòng)性的增強(qiáng)，我們的城市更容易發(fā)生“黑天鵝”事件，并且變得更加脆弱。例如，我們從這個(gè)模型可以發(fā)現(xiàn)在關(guān)鍵地區(qū)實(shí)施隔離制度或者采取嚴(yán)苛的措施來(lái)控制人員流動(dòng)能夠在疫情期間發(fā)揮巨大作用。

但還有一個(gè)十分重要的問(wèn)題就是，如何在執(zhí)行這些措施期間，使得城市功能和經(jīng)濟(jì)的損壞最小化?

此外，傳染病傳播機(jī)制也是一個(gè)活躍的研究領(lǐng)域，該領(lǐng)域的成果必須要滲透并整合到城市規(guī)劃、政策制定和城市管理當(dāng)中，以使我們的城市更安全更抗打擊。

上述模型代碼如下：

import numpy as np 
  # initialize the population vector from the origin-destination flow matrix 
  N_k = np.abs(np.diagonal(OD) + OD.sum(axis=0) - OD.sum(axis=1)) 
  locs_len = len(N_k)                 # number of locations 
  SIR = np.zeros(shape=(locs_len, 3)) # make a numpy array with 3 columns for keeping track of the S, I, R groups 
  SIR[:,0] = N_k                      # initialize the S group with the respective populations 
 
  first_infections = np.where(SIR[:, 0]<=thresh, SIR[:, 0]//20, 0)   # for demo purposes, randomly introduce infections 
  SIR[:, 0] = SIR[:, 0] - first_infections 
  SIR[:, 1] = SIR[:, 1] + first_infections                           # move infections to the I group 
 
  # row normalize the SIR matrix for keeping track of group proportions 
  row_sums = SIR.sum(axis=1) 
  SIRSIR_n = SIR / row_sums[:, np.newaxis] 
 
  # initialize parameters 
  beta = 1.6 
  gamma = 0.04 
  public_trans = 0.5                                 # alpha 
  R0 = beta/gamma 
  beta_vec = np.random.gamma(1.6, 2, locs_len) 
  gamma_vec = np.full(locs_len, gamma) 
  public_trans_vec = np.full(locs_len, public_trans) 
 
  # make copy of the SIR matrices  
  SIRSIR_sim = SIR.copy() 
  SIR_nSIR_nsim = SIR_n.copy() 
 
  # run model 
  print(SIR_sim.sum(axis=0).sum() == N_k.sum()) 
  from tqdm import tqdm_notebook 
  infected_pop_norm = [] 
  susceptible_pop_norm = [] 
  recovered_pop_norm = [] 
  for time_step in tqdm_notebook(range(100)): 
      infected_mat = np.array([SIR_nsim[:,1],]*locs_len).transpose() 
      OD_infected = np.round(OD*infected_mat) 
      inflow_infected = OD_infected.sum(axis=0) 
      inflow_infected = np.round(inflow_infected*public_trans_vec) 
      print('total infected inflow: ', inflow_infected.sum()) 
      new_infect = beta_vec*SIR_sim[:, 0]*inflow_infected/(N_k + OD.sum(axis=0)) 
      new_recovered = gamma_vec*SIR_sim[:, 1] 
      new_infect = np.where(new_infect>SIR_sim[:, 0], SIR_sim[:, 0], new_infect) 
      SIR_sim[:, 0] = SIR_sim[:, 0] - new_infect 
      SIR_sim[:, 1] = SIR_sim[:, 1] + new_infect - new_recovered 
      SIR_sim[:, 2] = SIR_sim[:, 2] + new_recovered 
      SIR_sim = np.where(SIR_sim<0,0,SIR_sim) 
      # recompute the normalized SIR matrix 
      row_sums = SIR_sim.sum(axis=1) 
      SIR_nsim = SIR_sim / row_sums[:, np.newaxis] 
      S = SIR_sim[:,0].sum()/N_k.sum() 
      I = SIR_sim[:,1].sum()/N_k.sum() 
      R = SIR_sim[:,2].sum()/N_k.sum() 
      print(S, I, R, (S+I+R)*N_k.sum(), N_k.sum()) 
      print('\n') 
      infected_pop_norm.append(I) 
      susceptible_pop_norm.append(S) 
      recovered_pop_norm.append(R) 

相關(guān)報(bào)道：

https://towardsdatascience.com/modelling-the-coronavirus-epidemic-spreading-in-a-city-with-python-babd14d82fa2

【本文是51CTO專(zhuān)欄機(jī)構(gòu)大數(shù)據(jù)文摘的原創(chuàng)譯文，微信公眾號(hào)“大數(shù)據(jù)文摘（ id: BigDataDigest）”】

戳這里，看該作者更多好文