前言

位運算在生產或算法解題中并不常見，不過如果你用得好，可以達到事半功倍的效果，而且位運算用得好，也可以極大地提升性能，如果在生產或面試中能看到使用位運算來解題，會讓人眼前一亮，覺得你還是有點逼格的，巧用位運算，不僅會提升性能，還會讓代碼的可讀性更好，達到四兩撥千斤的效果，今天我們就來學學位運算在解題中的一些技巧，最后會用位運算來看看怎么解八皇后這道大 Boss 題，相信你看完肯定會有收獲!

[[319856]]

本文將會從以下幾個方面來講解位運算

• 什么是位運算，位運算常見操作
• 位運算使用技巧簡介
• 巧用位運算解算法題

什么是位運算，位運算常見操作

在現(xiàn)代計算機中所有的數(shù)據(jù)在內存中都是以二進制存在的，位運算就是直接對整數(shù)在內存中的二進制位進行操作，由于位運算直接對內存數(shù)據(jù)進行操作，無需轉成十進制，因此使用位運算的處理速度是很快的。

舉個簡單的例子， 當我們要計算 6 & 4 的結果，在做位運算的時候首先要把 6，4 轉成二進制，然后再做相應的位操作(與)。

基本的位運算有與、或、異或、取反、左移、右移這6種，介紹如下：

& 與：只有當兩位都是 1 時結果才是 1，否則為 0 。

 0110 
&   0100 
----------- 
    0100 

| 或：兩位中只要有 1 位為 1 結果就是 1，兩位都為 0 則結果為 0。

 0110 
&   0110 
----------- 
    0110 

^ 異或：兩個位相同則為 0，不同則為 1

  0110 
^   0100 
----------- 
    0010 

~ 取反：0 則變?yōu)?1，1 則變?yōu)?0

~   0110 
----------- 
    1001 

<< 左移：向左進行移位操作，高位丟棄，低位補 0

int a = 8; 
a << 3; 
移位前：0000 0000 0000 0000 0000 0000 0000 1000 
移位后：0000 0000 0000 0000 0000 0000 0100 0000 

>> 右移：向右進行移位操作，對無符號數(shù)，高位補 0，對于有符號數(shù)，高位補符號位

unsigned int a = 8; 
a >> 3; 
移位前：0000 0000 0000 0000 0000 0000 0000 1000 
移位后：0000 0000 0000 0000 0000 0000 0000 0001 
 
int a = -8; 
a >> 3; 
移位前：1111 1111 1111 1111 1111 1111 1111 1000 
移位后：1111 1111 1111 1111 1111 1111 1111 1111 

位運算使用技巧簡介

接下來我們就由淺入深地來學習一下使用位運算的那些黑科技

1、 判斷整型的奇偶性

使用位運算操作如下

if((x & 1) == 0) { 
    // 偶數(shù) 
} else { 
    // 奇數(shù) 
} 

這個例子相信大家都見過，只需判斷整型的第一位是否是 1 即可，如果是說明是奇數(shù)，否則是偶數(shù)

2、 判斷第 n 位是否設置為 1

if (x & (1<<n)) { 
    // 第 n 位設置為 1 
} 
else { 
    // 第 n 位設置為 1 
} 

在上例中我們判斷第一位是否為 1，所以如果要判斷第 n 位是否 1，只要把 1 左移 n 位再作與運算不就完了。

3、將第 n 位設置為 1

y = x | (1<<n) 

思路同第二步，先把 1 移到第 n 位再作或運算，這樣第 n 位就肯定為 1。

4、將第 n 位設置為 0

y = x & ~(1< 

先將 1 左移到 第 n 位，再對其取反，此時第 n 位為 0，其他位都為 1，這樣與 x 作與運算后，x 的第 n 位肯定為 0。

5、將第 n 位的值取反

y = x ^ (1< 

我們知道異或操作是兩個數(shù)的每一位相同，結果為 0，否則是 1，所以現(xiàn)在把 1 左移到第 n 位，則如果 x 的第 n 位為 1，兩數(shù)相同結果 0，如果 x 的第 n 位為 0，兩數(shù)不相同，則為 1。來看個簡單的例子

01110101 
  00100000 
  -------- 
  01010101 

如圖示，第五位剛好取反

6、將最右邊的 1 設為 0

y = x & (x-1) 

如果說上面的 5 點技巧有點無聊，那第 6 條技巧確實很有意思，也是在 leetcode 經(jīng)常出現(xiàn)的考點，下文中大部分習題都會用到這個知識點，務必要謹記!掌握這個很重要，有啥用呢，比如我要統(tǒng)計 1 的位數(shù)有幾個，只要寫個如下循環(huán)即可，不斷地將 x 最右邊的 1 置為 0，最后當值為 0 時統(tǒng)計就結束了。

count = 0   
while(x) { 
  x = x & (x - 1); 
  count++; 
} 

先介紹這么多吧，如果大家對其他的位運算技巧感興趣可以看看文末的參考鏈接

巧用位運算解算法題

接下來我們看看位運算在算法題中的應用。

1、高頻面試題：老鼠試毒

有 8 個一模一樣的瓶子，其中有 7 瓶是普通的水，有一瓶是毒藥。任何喝下毒藥的生物都會在一星期之后死亡。現(xiàn)在，你只有 3 只小白鼠和一星期的時間，如何檢驗出哪個瓶子里有毒藥?

解題步驟如下：

（1）把這 8 個瓶子從 0 到 7 進行編號，用二進制表示如下

000 
001 
010 
011 
100 
101 
110 
111 

（2）將 0 到 7 編號中第一位為 1 的所有瓶子(即 1，3，5，7)的水混在一起給老鼠 1 吃，第二位值為 1 的所有瓶子(即2，3，6，7)的水混在一起給老鼠 2 吃， 第三位值為 1 的所有瓶子(4，5，6，7)的水混在一起給老鼠 3 吃，現(xiàn)在假設老鼠 1，3 死了，那么有毒的瓶子編號中第 1，3 位肯定為 1，老鼠 2 沒死，則有毒的瓶子編號中第 2 位肯定為 0，得到值 101 ，對應的編號是 5， 也就是第五瓶的水有毒。

這道題及其相關的變種在面試中出現(xiàn)地比較頻繁，比如我現(xiàn)在把 8 瓶水換成 1000 瓶，問你至少需要幾只老鼠才能測出有毒的瓶子，有了上述的思路相信應該不難，幾只老鼠就相當于幾個進制位，顯然 2^10 = 1024 > 1000，即 10 只老鼠即可測出來。

2、leetcode 232

給定一個數(shù)，判斷它是否是可以用 2 的冪次方表示，可以返回 true，不可以返回 false，比如 8 = 2^3, 說明可以用 2 的冪次方表示，返回 true，9 不可以，所以返回 false。

解題分析：這題常規(guī)解法是做個循環(huán)不斷地乘以 2 ，看下是否等于給定的值，如果等于說明是 2 的冪次方，否則如果不斷累乘 2 后大于給定的值，說明不能用 2 的冪次方表示，時間復雜度是所做的累乘的次數(shù)，即 2^n >= 給定的值中的 n。

那是否有更快的解法呢?

上文的介紹中其實我們已經(jīng)埋下伏筆了，沒錯用 x & (x-1)，首先我們要發(fā)現(xiàn)能用 2 的冪次方表示的數(shù)的特點：它的所有位中有且僅有一位為 1，如

00001        2^0 = 1 
00010        2^1 = 2 
00100        2^2 = 4 
01000        2^3 = 8 
10000        2^3 = 16 

如圖示，所有 2 的冪次方最多只有一位為 1

明白了這一點， 我們的思路就簡單了，由于符合 2 的冪次方的數(shù)只有一位為 1，x & (x-1) 是把最后一位 1 置為 0，所以只要做一次 x & (x-1) 運算，看它的值是否等于 0 即可，如果是 0 說明它可以用 2 的冪次方表示，否則不可以，代碼如下:

if(x&(x-1)) { //使用與運算判斷一個數(shù)是否是2的冪次方 
    printf("%d不是2的冪次方！\n", num); 
} else { 
    printf("%d是2的%d次方！\n", num, log2(num)); 
} 

只用一行代碼即可搞定，方便了很多!

3、leetcode 232

給定一個非負整數(shù) num. 對于 0 ≤ i ≤ num 范圍中的每個數(shù)字 i, 計算其二進制數(shù)中 1 的數(shù)目并將它們作為數(shù)組返回。輸入: 5 輸出: [0,1,1,2,1,2]

這題的常規(guī)解法相信大家都能猜到，就是從 0 到 num 循環(huán)一遍，求出每個數(shù)字 i 中 1 的數(shù)目。

如果用位運算怎么做呢，先來看下解法，然后我們再來分析為啥這樣寫，非常巧妙!

Python 代碼

vector<int> countBits(int num) { 
    vector<int> bits(num+1, 0); 
    for (int i = 1; i<= num; i++) { 
        bits[i] += bits[i & (i-1)] + 1; 
    } 
} 

Java 代碼

public static int[] countBits(int num) { 
    int[] bits = new int[num+1]; 
    Arrays.fill(bits, 0); 
 
    for (int i = 1; i <= num; i++) { 
        bits[i] = bits[i & (i-1)] + 1; 
    } 
    return bits; 
} 

最關鍵的代碼看這一行

bits[i] += bits[i & (i-1)] + 1; 

這行代碼是啥意思呢，i & (i-1) 是把 i 的最后一個值為 1 的位設為 0，不難發(fā)現(xiàn)整數(shù)「i & (i-1)」 中 1 的位數(shù)比 i 中 1 的位數(shù)少一個 ，所以要加 1(即 bits[i & (i-1)] + 1)。非常巧妙，這樣從 1 開始走一遍循環(huán)即可，中間不要做任何針對變量 i 的 1 的個數(shù)的計算，只不過付出了一個 bits 數(shù)組的代價。這里也是利用了以空間換時間的思想。

4、利用位運算來解八皇后問題

接下來我們來看看終級 Boss 題，如何用位運算來解八皇后問題，解題中運用到了非常多的位運算技巧，相信你學完會收獲不少。

在 8×8 格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處于同一行、同一列或同一斜線上，問有多少種擺法

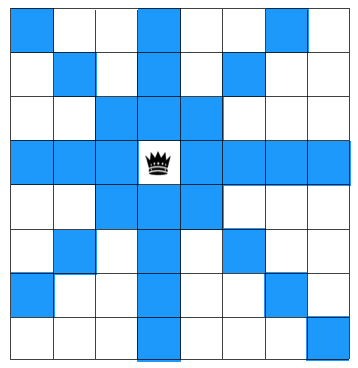
舉個簡單的下圖所示的例子，如果在棋盤上放置一個皇后，則與這個皇后同一行，同一列，且皇后所在斜線經(jīng)過的格子不能再放其他皇后。

如圖示，在其中任意一行放置一個皇后，則與此皇后同行，同列，同對角線的都不允許再放其他皇后，圖中藍色區(qū)塊不允許放其他皇后。

一般我們用回溯法解八皇后。這里簡單介紹一下啥是回溯法。

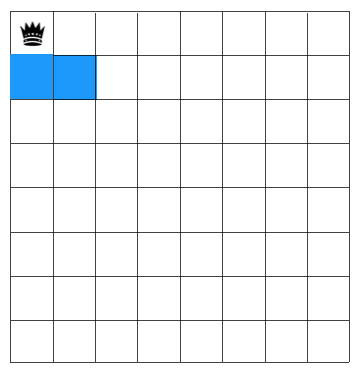
在第一行從左到右先選擇一個位置放置皇后，由于第一行放了皇后，第二行可放皇后的位置受到了限制(下圖藍色區(qū)塊表示對應行的格子不能放皇后)

如圖示,第二行放皇后的位置只能從第三個格子開始選

第二行我們選第三個格子放皇后，選完開始在第三行選，第三方可選的位置也受到了第一，二行皇后所放位置的影響

如圖示，第三行只能從第五個格子開始放置皇后

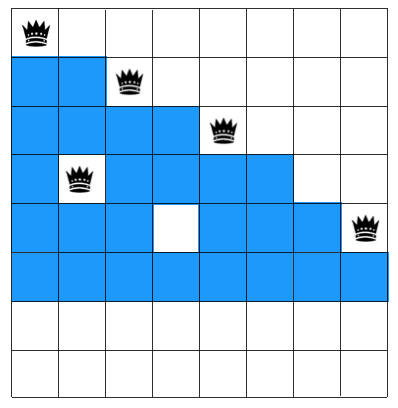
同理，第三，四，五行都從左到右選擇符合條件的的格子放置皇后，選完后問題來了，第六行所在行沒有可選的位置了!如圖示

怎么辦呢，回溯!重新擺放第五行的皇后，將其放到第八格上

重新擺放后發(fā)現(xiàn)第六行還是沒有符合條件的格子，咋辦，我們知道第六行可擺放皇后的格子受第五行影響，而第五行受第四行擺放皇后位置的影響的，所以回溯到第四行，將皇后位置擺放到當前行的其他位置(第七格)，再接著往下放 5，6，7，8 行的皇后。。。，只要不滿足條件，改變上一層的的條件重新來，上一層調整后還是不符合條件，再調整上上層的。。。，調整完后重新往下遞歸選擇，直到找到符合條件的，找到之后再在第一層換一個位置選皇后遞歸往下層選擇執(zhí)行，直到找到所有的解，這種不滿足條件就回退上層調整再試的思想就是回溯法，可以看到回溯法一般是用遞歸實現(xiàn)的。

回溯算法有不少變種，這里我們重點介紹使用位運算的回溯算法，它是所有解法中最高效的!如果在面試中能使用位運算來解回溯算法，絕對會讓面試官給你個大大的贊!

接下來是重點了，怎么用位運算來求解。

在以上回溯法的分析中，我們不難發(fā)現(xiàn)，在八皇后問題中，問題的關鍵是找出行可放皇后的格子。找到之后問題就解決了 90%，所以接下來我們就來看看怎么找這些可用的格子。

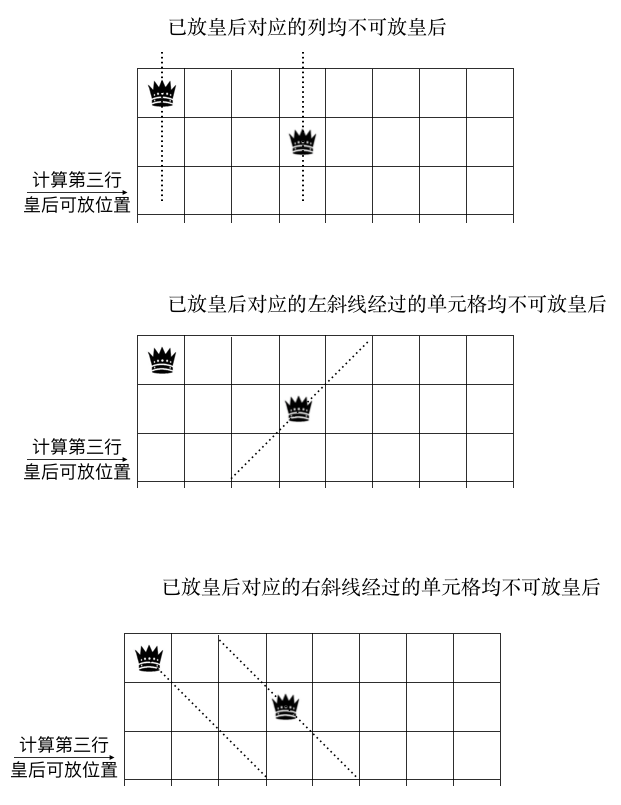
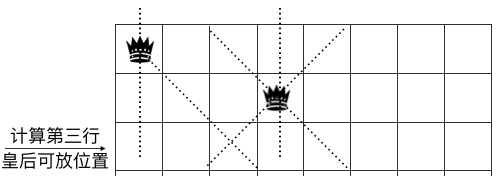
假設我們要求解第三行可放皇后的格子(說明一二行的皇后已放好了)那么第三行可放皇后的位置受到哪些條件的限制呢。顯然在第一二行已放皇后的格子所在的列，左斜線，右斜線對應的方格都不能放皇后，如圖示:

我們以 column 來記錄所有上方行已放置的皇后導致當前行格子不可用的集合，所在列如果放了皇后，則當前行格子對應的位置為 1，否則為 0，同理,以 pie(撇，左斜線) 記錄所有已放置的皇后左斜方向導致當前行格子不可用的集合， na(捺，右斜線) 表示所有已放置的皇后右斜方向導致當前行不可用的集合。則對于第三行來說我們有：

column = 10010000 (上圖中的第一個圖，第 1，4 列放了皇后，所以 1，4 位置為 1，其他位置為 0） 
pie = 00100000 (上圖中的第二個圖，左斜線經(jīng)過第三行的第三個方格，所以第三位為 1） 
na = 00101000 (上圖中的第三個圖，右斜線經(jīng)過第三行的第三, 五個方格，所以第三,五位為 1） 

將這三個變量作或運算得到結果如下

 10010000 
|   00100000 
|   00101000 
----------------------- 
    10111000 

也就是說對于第三層來說第 1，3，4，5 個格子不能放皇后。如圖示

于是可知 column | pie | na 得到的結果中值為 0 的代表當前行對應的格子可放皇后， 1 代表不能放，但我們想改成 1 代表格子可放皇后， 0 代表不可放皇后，畢竟這樣更符合我們的思維方式，怎么辦，取反不就行了，于是我們有~(column| pie | na)。

問題來了，這樣取反是有問題的，因為這三個變量都是定義的 int 型，為 32 位，取反之后高位的 0 全部變成了 1，而我們只想保留低 8 位(因為是 8 皇后)，想把高位都置為 0，怎么辦，這里就要用到位運算的黑科技了

~(column | pie | na) & ((1 << 8)-1) 

后面的的 ((1<< 8) -1) 表示先把 1 往左移 8 位，值為 100000000,再減 1 ，則低 8 位全部為 1，高位全部為 0!(即 0011111111)再作與運算，即可保留低 8 位，去除高位。

費了這么大的勁，我們終于把當前行可放皇后的格子都找出來了(所有位值為 1 的格子可放置皇后)。接下來我們只要做個循環(huán)，遍歷所有位為 1 的格子，每次取出可用格子放上皇后，再找下一層可放置皇后的格子，依此遞歸下去即可,直到所有行都遍歷完畢(遞歸的終止條件)。

還有一個問題，已知當前行的 column，pie，na，怎么確定下一行的 column，pie，na 的值(畢竟選完當前行的皇后后，要確定下一行的可用格子，而下一行的可用格子依賴于 column，pie，na 的值)

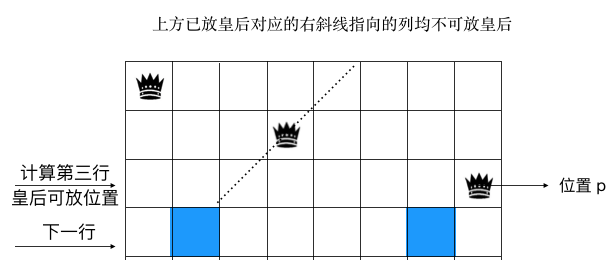
上文可知，我們已經(jīng)選出了當前行可用的格子(相應位為 1 對應的格子可用)，假設我們在當前行選擇了其中一個格子來放置皇后，此位置記為 p(如果是當前行的最后一個格子最后一個格子，則值為 1，如果放在倒數(shù)第二個，值為 10，倒數(shù)第三個則為 100，依此類推)，則對于下一行來說，顯然 column = column | p

那么 pie 呢，仔細看下圖，顯然應該為 (pie | p) << 1, 左斜線往下一行的格子延展時，相當于左移一位，

如圖示：下一行的 pie 顯然為 (pie | p) << 1。

同理 下一行的 na 為 (na | p) >> 1。

有了以上詳細地解析，我們就可以寫出偽代碼了

void queenSettle(row, colomn,pie,na) { 
    N = 8; // 8皇后 
    if (row >= N) { 
        // 遍歷到最后一行說明已經(jīng)找到符合的條件了 
        count++;return 
    } 
 
        // 取出當前行可放置皇后的格子 
    bits = (~(colomn|pie|na)) & ((1 << N)-1) 
 
    while(bits > 0) { 
            // 每次從當前行可用的格子中取出最右邊位為 1 的格子放置皇后 
            p = bits & -bits 
 
            // 緊接著在下一行繼續(xù)放皇后 
            queenSettle(row+1, colomn | p, (pie|p) << 1, (na | p) >> 1) 
 
            // 當前行最右邊格子已經(jīng)選完了，將其置成 0，代表這個格子已遍歷過 
            bits = bits & (bits-1) 
    } 
} 

一開始傳入 queenSettle(0,0,0,0) 這樣即可得到最終的解。偽代碼寫得很清楚了，相信用相關語言不難實現(xiàn)，這里就留給大家作個練習吧。

總結

本文帶大家由淺入深地完成了位運算的學習，掌握好位運算不僅僅是為了提升逼格，還能極大地提升效率，位運算也廣泛地應用于代碼編寫中，運用得當能極大地簡化代碼，且可讀性更好，限于篇幅關系，這里不展開，大家如有興趣可參考文末的鏈接。

如有幫助，歡迎大家關注公號哦。之后將會講解大量算法的解題思路，希望我們一起攻克算法難題!