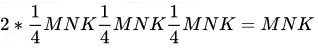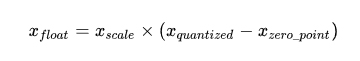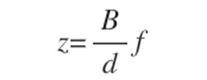引言

氣象預(yù)報、石油勘探、核子物理等現(xiàn)代科學(xué)技術(shù)大多依賴計算機(jī)的計算模擬，模擬計算的核心是表示狀態(tài)轉(zhuǎn)移的矩陣計算。另一方面，計算機(jī)圖形處理以及近年來興起的深度學(xué)習(xí)也和矩陣乘高度相關(guān)。而矩陣乘對計算資源消耗較大，除了計算機(jī)體系結(jié)構(gòu)的不斷更新外，軟件優(yōu)化方面也有大量的研究工作。

本文簡要介紹通用矩陣乘（GEMM，General Matrix Multiplication）優(yōu)化的基本概念和方法、QNNPACK 對特定場景的矩陣乘的優(yōu)化方法、以及用 GEMM 優(yōu)化神經(jīng)網(wǎng)絡(luò)中卷積計算的一點方向。

旨在幫助大家在概念中建立一些直覺，無甚高論。

通用矩陣乘優(yōu)化

基本概念

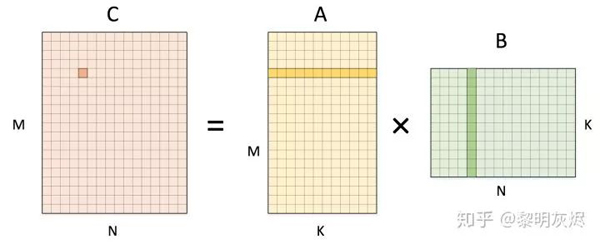
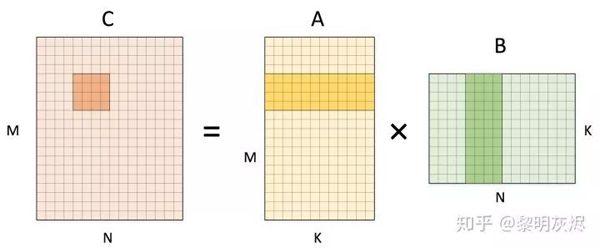
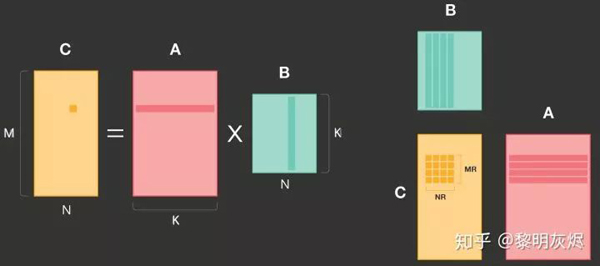
通用矩陣乘（下文簡稱 GEMM）的一般形式是 𝐶=𝐴𝐵C=AB， 其中 𝐴A 和 𝐵B 涵蓋了各自轉(zhuǎn)置的含義。圖一是矩陣乘計算中為計算一個輸出點所要使用的輸入數(shù)據(jù)。三個矩陣的形狀也如圖所示。

圖一：矩陣乘一個輸出元素的計算

該計算的偽代碼如下。該計算操作總數(shù)為  （其中 𝑀、𝑁、𝐾 分別指代三層循環(huán)執(zhí)行的次數(shù)，2 指代循環(huán)最內(nèi)層的一次乘法和加法） ，內(nèi)存訪問操作總數(shù)為 4𝑀𝑁𝐾（其中 4 指代對 𝐴、𝐵、𝐶 三者的內(nèi)存訪問，𝐶 需要先讀取內(nèi)存、累加完畢在存儲，且忽略對 𝐶 初始化時的操作）。GEMM 的優(yōu)化均以此為基點。 

for (int m = 0; m < M; m++) {  
  for (int n = 0; n < N; n++) {  
    C[m][n] = 0;  
    for (int k = 0; k < K; k++) {  
      C[m][n] += A[m][k] * B[k][n];  
    }  
  }  
} 

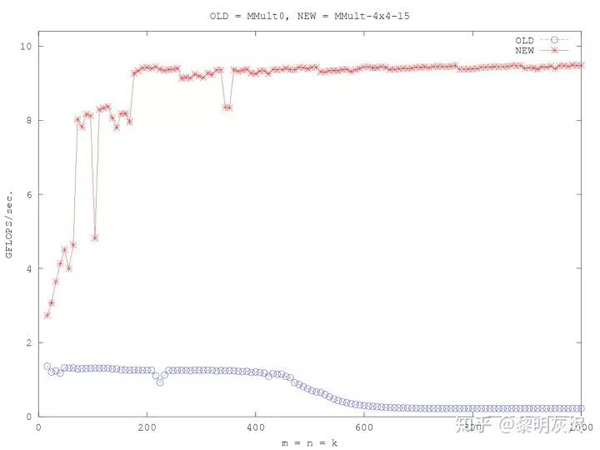
How to optimize gemm （https://github.com/flame/how-to-optimize-gemm/wiki）介紹了如何采用各種優(yōu)化方法，將最基礎(chǔ)的計算改進(jìn)了約七倍（如圖二）。其基本方法是將輸出劃分為若干個 4×4子塊，以提高對輸入數(shù)據(jù)的重用。同時大量使用寄存器，減少訪存；向量化訪存和計算；消除指針計算；重新組織內(nèi)存以地址連續(xù)等。詳細(xì)的可以參考原文。

圖二：How to optimize gemm 的優(yōu)化效果

計算拆分展示

本節(jié)主要以圖形化的方式介紹計算拆分。

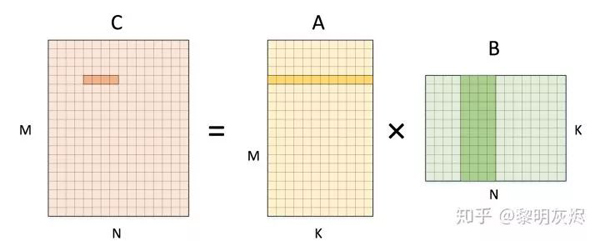
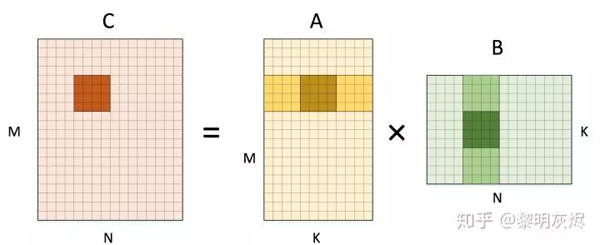
圖三 將輸出的計算拆分為 1×4 的小塊，即將 𝑁 維度拆分為兩部分。計算該塊輸出時，需要使用 𝐴 矩陣的 1 行，和 𝐵 矩陣的 4 列。

圖三：矩陣乘計算 1×4輸出

下面是該計算的偽代碼表示，這里已經(jīng)將 1×4 中 𝑁N 維度的內(nèi)部拆分進(jìn)行了展開。這里的計算操作數(shù)仍然是 2𝑀𝑁𝐾 ，這一點在本文中不會有變化。這里的內(nèi)存訪問操作數(shù)尚未出現(xiàn)變化，仍然是 4𝑀𝑁𝐾，但接下來會逐步改進(jìn)。 

for (int m = 0; m < M; m++) {  
  for (int n = 0; n < N; n += 4) {  
    C[m][n + 0] = 0;  
    C[m][n + 1] = 0;  
    C[m][n + 2] = 0;  
    C[m][n + 3] = 0;  
    for (int k = 0; k < K; k++) {  
      C[m][n + 0] += A[m][k] * B[k][n + 0];  
      C[m][n + 1] += A[m][k] * B[k][n + 1];  
      C[m][n + 2] += A[m][k] * B[k][n + 2];  
      C[m][n + 3] += A[m][k] * B[k][n + 3];  
    }  
  }  
} 

簡單的觀察即可發(fā)現(xiàn)，上述偽代碼的最內(nèi)側(cè)計算使用的矩陣 𝐴 的元素是一致的。因此可以將 𝐴[𝑚][𝑘] 讀取到寄存器中，從而實現(xiàn) 4 次數(shù)據(jù)復(fù)用（這里不再給出示例）。一般將最內(nèi)側(cè)循環(huán)稱作計算核（micro kernel）。進(jìn)行這樣的優(yōu)化后，內(nèi)存訪問操作數(shù)量變?yōu)?(2+1/4)𝑀𝑁𝐾，其中 1/4是對 𝐴 優(yōu)化的效果。

類似地，我們可以繼續(xù)拆分輸出的 𝑀 維度，從而在內(nèi)側(cè)循環(huán)中計算 4×4 輸出，如圖四。

圖四：矩陣乘計算 4×44×4輸出

同樣地，將計算核心展開，可以得到下面的偽代碼。這里我們將 1×4 中展示過的 𝑁 維度的計算簡化表示。這種拆分可看成是 4×1×4，這樣 𝐴 和 𝐵 的訪存均可復(fù)用四次。由于乘數(shù)效應(yīng)，4×4 的拆分可以將對輸入數(shù)據(jù)的訪存縮減到 2𝑀𝑁𝐾+1/4𝑀𝑁𝐾+1/4𝑀𝑁𝐾=(2+1/2)𝑀𝑁𝐾)。這相對于最開始的 4𝑀𝑁𝐾 已經(jīng)得到了 1.6X 的改進(jìn)，這些改進(jìn)都是通過展開循環(huán)后利用寄存器存儲數(shù)據(jù)減少訪存得到的。 

for (int m = 0; m < M; m += 4) {  
  for (int n = 0; n < N; n += 4) {  
    C[m + 0][n + 0..3] = 0;  
    C[m + 1][n + 0..3] = 0;  
    C[m + 2][n + 0..3] = 0;  
    C[m + 3][n + 0..3] = 0;  
    for (int k = 0; k < K; k++) {  
      C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];  
      C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];  
      C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];  
      C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];  
    }  
  }  
} 

到目前為止，我們都是在輸出的兩個維度上展開，而整個計算還包含一個削減（Reduction）維度 𝐾。圖五展示了在計算 4×4 輸出時，將維度 𝐾 拆分，從而每次最內(nèi)側(cè)循環(huán)計算出輸出矩陣 𝐶 的 4x4 部分和。

圖五：矩陣乘計算 4×4 輸出對 𝐾 維度的拆分

下面展示的是這部分計算的展開偽代碼，其中維度 𝑀 和 𝑁 已經(jīng)被簡寫。在這里，最內(nèi)側(cè)循環(huán)發(fā)生的計算次數(shù)已經(jīng)從最樸素版本的  發(fā)展到了  。 

for (int m = 0; m < M; m += 4) {  
  for (int n = 0; n < N; n += 4) {  
    C[m + 0..3][n + 0..3] = 0;  
    C[m + 0..3][n + 0..3] = 0;  
    C[m + 0..3][n + 0..3] = 0;  
    C[m + 0..3][n + 0..3] = 0;  
    for (int k = 0; k < K; k += 4) {  
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];  
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];  
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3];  
      C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];  
    }  
  }  
} 

在對 𝑀 和 𝑁 展開時，我們可以分別復(fù)用 𝐵 和 𝐴 的數(shù)據(jù)；在對 𝐾 展開時，我們可以將部分和累加在寄存器中，最內(nèi)層循環(huán)一次迭代結(jié)束時一次寫到 𝐶 的內(nèi)存中。那么內(nèi)存訪問次數(shù)為   

——相對原始實現(xiàn)的 4X 改進(jìn)！

到目前為止，我們已經(jīng)對計算進(jìn)行了三次維度拆分、展開并寄存器化（代碼未展示）和訪存復(fù)用。這對最基礎(chǔ)版本計算似乎已經(jīng)足夠了，因為數(shù)百條穩(wěn)定的順序計算指令對處理器流水線已經(jīng)很友好，且編譯器可以幫助我們做好軟件流水這樣的指令調(diào)度。

然而一條計算指令只能完成一次乘加操作（MLA）效率還是比較低。實際上即使是最低端的移動手機(jī)處理器都會帶有 SIMD 支持，訪存和計算都可以向量化。因此我們可以再進(jìn)一步，利用向量操作提高計算的性能。

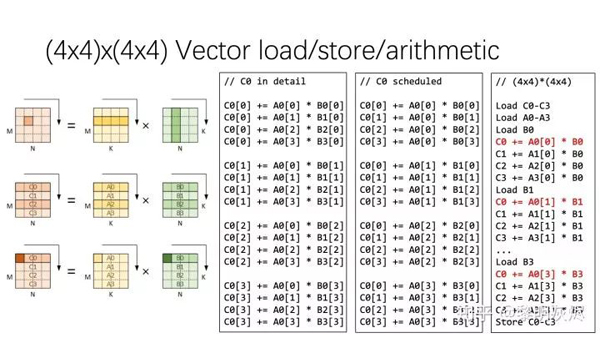
在介紹向量化計算的細(xì)節(jié)時，偽代碼是很難理解的，下面依據(jù)圖六介紹量化計算的具體過程。圖六左側(cè)部分的三幅小圖分別展示了兩個 4×4 矩陣相乘向量化的要素：首先是計算一個輸出元素使用到的輸入元素；然后是對各個矩陣內(nèi)存的編碼，均以行優(yōu)先的形式編號；最后是向量化的具體計算方法。

圖六：兩個 4×4矩陣相乘的向量化

這里的向量編號方式假定輸入輸出的內(nèi)存布局都是行優(yōu)先，那么兩個輸入各自的 16 個元素通過 4 次向量訪存即可加載到寄存器中。由矩陣乘的規(guī)則可知，輸入 𝐴 中的行可一次性用作輸出的計算，而輸入 𝐵B 的行則要拆分使用。這也是向量計算最容易出錯的地方。

圖六右側(cè)列出了三份偽代碼。第一份 C0 in detail 是計算 C0 中四個輸出元素的樸素方法的展開，連續(xù)四次計算得到一個 C0 元素的結(jié)果。將計算過程稍作重排，即可得到 C0 scheduled 展示的計算，這里連續(xù)的四次計算分別處理了 C0 中四個元素的 1/4 結(jié)果。在連續(xù)的四次計算中，重排前只有對 𝐴A 的訪存是連續(xù)的，重排后 𝐵 和 𝐶 的訪存都是連續(xù)的。那么向量化這些訪存和計算，即可得到第三列偽代碼中紅色 C0 部分。而第三列是通過對 C1、C2、C3 進(jìn)行類似的處理得到的。

施行向量化操作后，原本需要 64 條計算指令的計算過程所需指令減少到 16 條，訪存也有類似效果。而向量化對處理器資源的高效使用，又帶來了進(jìn)一步優(yōu)化空間，例如可以一次計算 8×8 個局部輸出。

處理內(nèi)存布局

上一小節(jié)列出的是在輸入輸出原有內(nèi)存布局上所做的優(yōu)化。在最后向量化時，每次內(nèi)存訪問都是四個元素。當(dāng)這些元素為單精度浮點數(shù)時，內(nèi)存大小為 16 字節(jié)，這遠(yuǎn)小于現(xiàn)代處理器高速緩存行大小（Cache line size）——后者一般為 64 字節(jié)。在這種情況下，內(nèi)存布局對計算性能的影響開始顯現(xiàn)。

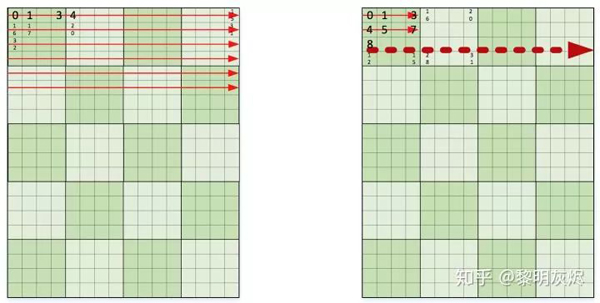
圖七展示的是不同內(nèi)存組織方式對的影響。圖中兩者都是行優(yōu)先的內(nèi)存排列，區(qū)別在于左側(cè)小方塊內(nèi)部是不連續(xù)的，右側(cè)小方塊內(nèi)部是連續(xù)的。圖中用幾個數(shù)字標(biāo)記了各個元素在整個內(nèi)存中的編號。

圖七：不同的局部內(nèi)存組織

想象一下在這兩者不同內(nèi)存組織方式的輸入輸出中訪存，每次向量化內(nèi)存加載仍是 4 個元素。對于一個局部計算使用到的小方塊，左側(cè)四次訪存的內(nèi)存都是不連續(xù)的，而右側(cè)則是連續(xù)的。當(dāng)數(shù)據(jù)規(guī)模稍大（一般情況肯定足夠大了），左側(cè)的連續(xù)四次向量化內(nèi)存加載都會發(fā)生高速緩存缺失（cache miss），而右側(cè)只會有一次缺失。

在常規(guī)的數(shù)據(jù)規(guī)模中，由于左側(cè)會發(fā)生太多的高速緩存缺失，又由于矩陣乘這樣的計算對數(shù)據(jù)的訪問具有很高的重復(fù)性，將它重排成右側(cè)的內(nèi)存布局減少高速緩存缺失，可顯著地改進(jìn)性能。另一方面，矩陣乘中兩個輸入矩陣往往有一個是固定的參數(shù)，在多次計算中保持不變。那么可以在計算開始前將其組織成特定的形狀，這種優(yōu)化甚至可以將性能提高 2x。

到這里為止，對 4×4 計算已經(jīng)有了足夠的優(yōu)化，可以開始考慮視野更廣一些的全局優(yōu)化。圖八是一個關(guān)于全局優(yōu)化的小示例。

圖八：矩陣乘的全局優(yōu)化一瞥

圖中字母標(biāo)記的是全局性的工作順序，即輸出數(shù)據(jù)中外層循環(huán)迭代方式。左側(cè)小圖是常規(guī)的行優(yōu)先遍歷方式，中間小圖是列有限的遍歷方式。這兩者的區(qū)別是 𝑀 和 𝑁 兩個維度的循環(huán)哪個在最外層。

上文已經(jīng)對 𝑀 和 𝑁 兩個維度分別進(jìn)行了一次拆分，這里可以繼續(xù)這種拆分。右側(cè)的圖例中是將 𝑀 和 𝑁 兩個維度分別拆分為 𝑋,2,4 三部分，將外層拆分都交換到外層循環(huán)。下面是相應(yīng)的偽代碼。 

for (int mo = 0; mo < M; mo += 8) {  
  for (int no = 0; no < N; no += 8) {  
    for (int mi = 0; mi < 2;mi ++) {  
      for (int ni = 0; ni < 2; ni++) {  
        int m = mo + mi * 4;  
        int n = no + ni * 4;  
        C[m + 0..3][n + 0..3] = 0;  
        C[m + 0..3][n + 0..3] = 0;  
        C[m + 0..3][n + 0..3] = 0;  
        C[m + 0..3][n + 0..3] = 0;  
        for (int k = 0; k < K; k += 4) {  
          C[m + 0..3][n + 0..3] += A[m + 0..3][k + 0] * B[k + 0][n + 0..3];  
          C[m + 0..3][n + 0..3] += A[m + 0..3][k + 1] * B[k + 1][n + 0..3];  
          C[m + 0..3][n + 0..3] += A[m + 0..3][k + 2] * B[k + 2][n + 0..3]; 
          C[m + 0..3][n + 0..3] += A[m + 0..3][k + 3] * B[k + 3][n + 0..3];  
        }  
      }  
    }  
  }  
} 

經(jīng)過這樣的調(diào)度，從整體計算來看，可看作是將 4×4 計算拓展成了 8×8 ，其實是同一種思路。

QNNPACK 的矩陣乘優(yōu)化

QNNPACK (Quantized Neural Network PACKage) 是 Facebook 開源的專門用于量化神經(jīng)網(wǎng)絡(luò)的計算加速庫。QNNPACK 和 NNPACK (Neural Network PACKage) 的作者都是 Marat Dukhan 。到目前為止，QNNPACK 仍然是已公開的，用于移動端（手機(jī)）的，性能最優(yōu)的量化神經(jīng)網(wǎng)絡(luò)加速庫。

QNNPACK 開源時附帶了一份技術(shù)報告性質(zhì)的博客。本節(jié)將結(jié)合上節(jié)的內(nèi)容簡要地從博客原作中抽取一些關(guān)于 GEMM 的內(nèi)容。

量化神經(jīng)網(wǎng)絡(luò)

神經(jīng)網(wǎng)絡(luò)計算一般都是以單精度浮點（Floating-point 32, FP32）為基礎(chǔ)。而網(wǎng)絡(luò)算法的發(fā)展使得神經(jīng)網(wǎng)絡(luò)對計算和內(nèi)存的要求越來越大，以至于移動設(shè)備根本無法承受。為了提升計算速度，量化（Quantization）被引入到神經(jīng)網(wǎng)絡(luò)中，主流的方法是將神經(jīng)網(wǎng)絡(luò)算法中的權(quán)重參數(shù)和計算都從 FP32 轉(zhuǎn)換為 INT8 。

兩種數(shù)值表示方法的方程如上。如果對量化技術(shù)的基本原理感興趣，可以參考 Neural Network Quantization Introduction 。

應(yīng)用量化技術(shù)后，計算方面顯現(xiàn)了若干個新的問題。首先是 NNPACK 這樣用于 FP32 的計算加速庫無法用于 INT8 ，這導(dǎo)致我們需要新的加速計算方法。再者是輸入輸出都轉(zhuǎn)化成 INT8 后，內(nèi)存帶寬需求直接下降為 1/4 。隨之而來的內(nèi)存容量需求變化出現(xiàn)了一些新的優(yōu)化機(jī)會。而 QNNPACK 充分利用了這些優(yōu)化方法，并結(jié)合神經(jīng)網(wǎng)絡(luò)領(lǐng)域的特點，大幅改進(jìn)了計算性能。

另一方面，Gemmlowp 是 Google 開源的低精度 GEMM 加速庫。在加速之外，Gemmlowp 的特別之處是提供了一套用定點計算模擬浮點計算的機(jī)制。例如  這樣浮點計算也可通過 Gemmlowp 在僅支持定點計算的處理器上運行。和 QNNPACK 不同，Gemmlowp 似乎目的在于支持 GEMM 而非單純神經(jīng)網(wǎng)絡(luò)，因此在神經(jīng)網(wǎng)絡(luò)方面的性能目前落后于 QNNPACK 。

計算劃分與削減維度

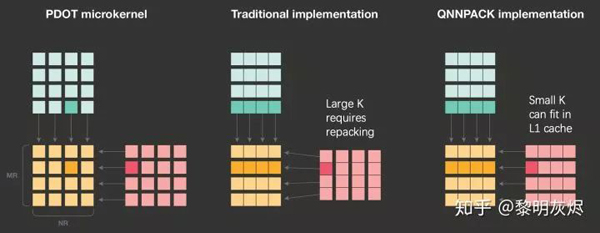
和上節(jié)所述類似，QNNPACK 的計算也是基于對輸出的劃分，拆分成如圖九的 𝑀𝑅×𝑁𝑅MR×NR 小塊。這里需要注意的一點是，原文圖例中對 𝐵B 的標(biāo)記有筆誤，𝐵B 的列高度應(yīng)該是 𝐾K 而非 𝑁N。（我們向 QNNPACK 報告了這一問題，目前尚未得到修正。）

圖九：QNNPACK 矩陣乘劃分示例

QNNPACK 實現(xiàn)了 4×8 的和 8×8 兩種計算核（micro kernel），分別用于支持 armv7 和 arm64 指令集的處理器。這兩種計算核在原理上區(qū)別不大，后者主要利用了更多的寄存器和雙發(fā)射（Dual Issue）以提高計算的并行度。

拆分后 𝑀𝑅×𝑁𝑅 計算塊使用的內(nèi)存為 𝑀𝑅∗𝑁𝑅+𝑀𝑅∗𝐾+𝑁𝑅∗𝐾。由于常規(guī)的神經(jīng)網(wǎng)絡(luò)計算 𝐾<1024 ， 那么這里的內(nèi)存消耗一般不超過 16KB，可以容納在一級高速緩存（L1 Cache）中。QNNPACK 的這一發(fā)現(xiàn)是其矩陣乘優(yōu)化的基礎(chǔ)。

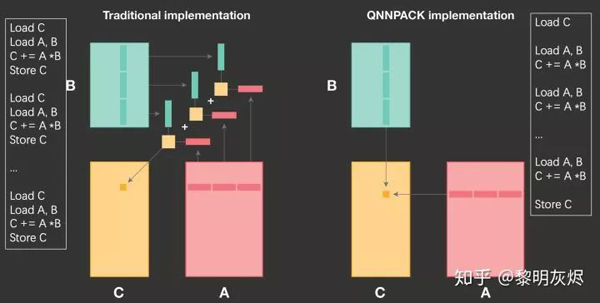
如圖十所示，在計算 𝑀𝑅×𝑁𝑅 小塊時，傳統(tǒng)的方法（即上一節(jié)的方法）是在 𝐾 維度上拆分，在一次計算核的處理中，僅計算 𝐾 維的局部。那么在每次計算核的處理中，都會發(fā)生對輸出的加載和存儲——要將本次計算產(chǎn)生的部分和累加到輸出中。

圖十：QNNPACK 和傳統(tǒng)方法計算削減維度的對比

而 QNNPACK 的做法是將整個 𝐾K 維全部在計算核中處理完，這樣就幾乎完全消除了輸出部分和的訪存。兩種的差異的細(xì)節(jié)可以參考圖十兩側(cè)的偽代碼。這里所說的「將整個 𝐾 維全部」并不是指 𝐾 維不拆分——在實際計算中 𝐾K 維還是會以 8 為基礎(chǔ)拆分——而是指拆分后不和其他維度交換（interchange）。

內(nèi)存組織的特點

上節(jié)中曾提到，對內(nèi)存的重新組織（Repacking）可以改進(jìn)高速緩存命中率，從而提高性能。但是這種重新組織也是有開銷的。

計算核中最小的計算單元處理的是兩個 4×4 矩陣相乘。傳統(tǒng)的方法由于 𝐾 可能很大，需要對輸入內(nèi)存進(jìn)行重新組織，防止相鄰的訪存引起高速緩存沖突，如圖十一。

圖十一：QNNPACK 和傳統(tǒng)矩陣乘對局部計算的處理

而在量化神經(jīng)網(wǎng)絡(luò)中，由于 𝐾K 比較小，計算核處理中使用到的內(nèi)存完全可以容納在一級高速緩存中，即使不重新組織內(nèi)存，高速緩存的重用率也足夠高。

參考圖七左側(cè)部分，QNNPACK 計算核一次會使用 8 行輸入（假定圖中繪制以 8 為基礎(chǔ)分塊）。盡管對第一個 8×8 矩陣塊的向量化加載可能全部是高速緩存缺失（Cache miss），第二個 8×8 則全部命中——因為它們已經(jīng)作為同在一個高速緩存行的內(nèi)容隨第一個矩陣塊加載到了高速緩存中。其他矩陣塊也是類似情況。

采用了這些基于神經(jīng)網(wǎng)絡(luò)領(lǐng)域先驗知識的優(yōu)化方法后，QNNPACK 擊敗了所有神經(jīng)網(wǎng)絡(luò)量化領(lǐng)域的用于移動端加速庫。不過，QNNPACK 的拆分著眼于削減維度，沒有在輸出維度上做全局調(diào)度。我們在 QNNPACK 基礎(chǔ)上實現(xiàn)了 𝑀 和 𝑁 維度的外層循環(huán)拆分調(diào)度，簡單的實驗獲得了相對于 QNNPACK 1.1x 的性能表現(xiàn)。

卷積與矩陣乘

卷積（Convolution）是神經(jīng)網(wǎng)絡(luò)的核心計算。而卷積的變種極為豐富，本身計算又比較復(fù)雜，因此其優(yōu)化算法也多種多樣，包括 im2col、Winograd 等等。本節(jié)重點關(guān)注卷積和矩陣乘的關(guān)系。

im2col 計算方法

作為早期的深度學(xué)習(xí)框架，Caffe 中卷積的實現(xiàn)采用的是基于 im2col 的方法，至今仍是卷積重要的優(yōu)化方法之一。

im2col 是計算機(jī)視覺領(lǐng)域中將圖片的不同通道（channel）轉(zhuǎn)換成矩陣的列（column）的計算過程。Caffe 在計算卷積時，首先用 im2col 將輸入的三維數(shù)據(jù)轉(zhuǎn)換成二維矩陣，使得卷積計算可表示成兩個二維矩陣相乘，從而充分利用已經(jīng)優(yōu)化好的 GEMM 庫來為各個平臺加速卷積計算。

圖十二是卷積的 im2col 過程的示例。隨著卷積過濾器在輸入上滑動，將被使用的那部分輸入展開成一行大小為 𝐼𝐶×𝐾𝐻×𝐾𝑊 的向量。在滑動結(jié)束后，則得到特征矩陣 (𝐻×𝑊)×(𝐼𝐶×𝐾𝐻×𝐾𝑊) 。將過濾器展開成 (𝑂𝐶)×(𝐼𝐶×𝐾𝐻×𝐾𝑊) 的矩陣，那么卷積即可表示成這兩個矩陣相乘的結(jié)果（特征矩陣要進(jìn)行轉(zhuǎn)置操作）。

圖十二：im2col 過程

im2col 計算卷積使用 GEMM 的代價是額外的內(nèi)存開銷，輸入會使用額外的 𝐾𝐻×𝐾𝑊 倍內(nèi)存。當(dāng)卷積核尺寸是 1×1 時，由于不需要重排輸入，GEMM 可以直接在原始輸入上運行，并且不需要使用額外的內(nèi)存。

內(nèi)存布局與卷積性能

神經(jīng)網(wǎng)絡(luò)中卷積的內(nèi)存布局主要有 NCHW 和 NHWC 兩種。最后重點分析一下 im2col 1×1 卷積性能和內(nèi)存布局的關(guān)系。

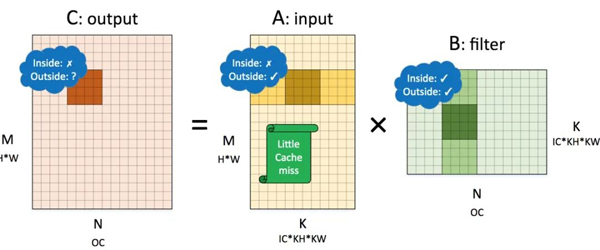
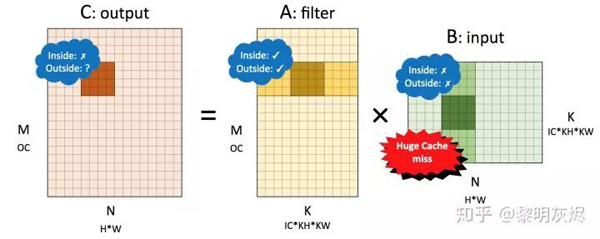
對于不需要額外調(diào)整輸入的 1×1 卷積，將 NCHW 內(nèi)存布局的卷積對應(yīng)到矩陣乘 𝐶=𝐴𝐵 時，𝐴 是卷積核（filter），𝐵 是輸入（input）。各個矩陣的維度如圖十二所示。

圖十二：NCHW 內(nèi)存布局卷積轉(zhuǎn)換成的矩陣乘

對該矩陣施行劃分后，將計算核的訪存局部性表現(xiàn)標(biāo)記在圖十二中。其中 Inside 表示小塊矩陣乘內(nèi)部的局部性，Outside 表示在削減維度方向的局部性。

對輸出而言，小塊內(nèi)向量化訪存局部性較差，外部表現(xiàn)取決于全局計算方向——行優(yōu)先則局部性較好，列優(yōu)先則較差。由于卷積核可以事先重排內(nèi)存，因此視其局部性都較好。輸入則小塊內(nèi)外都較差，因為削減維度是列優(yōu)先的，幾乎每次加載輸入都會發(fā)生高速緩存缺失。

圖十三是與之相對的 NHWC 內(nèi)存布局的示例。值得注意的是，NHWC 和 NCHW 中 𝐴、𝐵 矩陣所代表的張量發(fā)生了調(diào)換——𝑂𝑢𝑡𝑝𝑢𝑡=𝐼𝑛𝑝𝑢𝑡×𝐹𝑖𝑙𝑡𝑒𝑟。具體的拆分方式仍然一樣。

圖十三：NHWC 內(nèi)存布局卷積轉(zhuǎn)換成的矩陣乘

在 NHWC 中，輸出的局部性表現(xiàn)和 NCHW 一樣。同樣的，卷積核也視作局部性表現(xiàn)較好。對于輸入，小方塊的內(nèi)部局部性表現(xiàn)不是很好，因為幾次向量加載的地址不連續(xù)；而外部局部性表現(xiàn)則較好，因為在削減維度滑動使用的內(nèi)存是連續(xù)的——這一點在「處理內(nèi)存布局」小節(jié)中已有闡述。

可以看到，對于 1×1如果采用 im2col 方法計算，且不對輸入輸出進(jìn)行額外的內(nèi)存重排，那么 NHWC 的訪存特征是顯著優(yōu)于 NCHW 的。

總結(jié)

至此，本文介紹了 GEMM 優(yōu)化的基本方法概念，在神經(jīng)網(wǎng)絡(luò)領(lǐng)域中 QNNPACK 基于量化對 GEMM 的優(yōu)化，和 im2col 方法對卷積計算及其內(nèi)存布局的意義。GEMM 優(yōu)化實質(zhì)上是個非常重要，且和特定領(lǐng)域綁定很強(qiáng)的話題，更進(jìn)一步的內(nèi)容需要進(jìn)入到特定領(lǐng)域深入研究。如果對 GEMM 各種優(yōu)化技巧所帶來的性能收益感興趣，可以參考 How to optimize gemm。如果對 GEMM 優(yōu)化和體系結(jié)構(gòu)結(jié)合的理論感興趣，可以參考 Anatomy of High-Performance Matrix Multiplication 。