1. 摘要

排序模型在廣告、推薦和搜索系統(tǒng)中起到了至關(guān)重要的作用。在排序模塊中，點擊率預估技術(shù)又是重中之重。目前工業(yè)界的點擊率預估技術(shù)大多采用深度學習算法，基于數(shù)據(jù)驅(qū)動來訓練深度神經(jīng)網(wǎng)絡，然而數(shù)據(jù)驅(qū)動帶來的相應問題是推薦系統(tǒng)中的新進項目會存在冷啟動問題。

探索與利用（Exploration-Exploitation，E&E）方法通常用于處理大規(guī)模在線推薦系統(tǒng)中的數(shù)據(jù)循環(huán)問題。過去的研究通常認為模型預估不確定度高意味著潛在收益也較高，因此大部分研究文獻聚焦到對不確定度的估計上。對于采用流式訓練的在線推薦系統(tǒng)而言，探索策略會對訓練樣本的收集產(chǎn)生較大影響，進而影響模型的進一步學習。然而，當前大多數(shù)探索策略并不能很好的建模被探索的樣本如何對后續(xù)模型學習產(chǎn)生影響。因此，我們設計了一個擬探索（Pseudo-Exploration） 模塊來模擬樣本被成功探索并展現(xiàn)后對推薦模型后續(xù)學習的影響。

擬探索過程通過在模型輸入中添加對抗擾動來實現(xiàn)，我們同時也給出了該過程相應的理論分析以及證明。基于此，我們將該方法命名為基于對抗梯度的探索策略（ A dversarial G radient driven E xploration，以下簡稱 AGE ）。為了提高探索的效率，我們還提出了一個動態(tài)門控單元用來過濾低價值樣本，避免將資源浪費在低價值的探索上。為了驗證AGE算法的有效性，我們不僅在公開學術(shù)數(shù)據(jù)集上進行了大量的實驗，也將AGE模型部署到了阿里媽媽展示廣告平臺上并取得了良好的線上收益。該工作已被KDD 2022 Research Track收錄為Full Paper，歡迎閱讀交流。

論文： Adversarial Gradient Driven Exploration for Deep Click-Through Rate Prediction

下載： https://arxiv.org/abs/2112.11136

2. 背景

在廣告系統(tǒng)中，點擊率（CTR）預估模型通常采用流式方式加以訓練，而流式數(shù)據(jù)的來源又是由部署在線上的CTR模型產(chǎn)出，這就產(chǎn)生了所謂的 數(shù)據(jù)循環(huán) 問題。冷啟動與長尾廣告由于沒有充分展現(xiàn)，CTR模型缺乏對這部分廣告的訓練數(shù)據(jù)，這也導致模型對這部分廣告的估計可能存在較大誤差，會使得這些廣告更加難以展現(xiàn)，進而難以完成冷啟動過程。具體而言，圖一給出了廣告真實點擊率與展現(xiàn)數(shù)量之間的關(guān)系：我們系統(tǒng)中，一個新廣告的展現(xiàn)平均需要達到約一萬次，其點擊率才能達到收斂態(tài)。這給許多在線系統(tǒng)帶來了一個常見的難題，即如何在保證用戶體驗的前提下，為這些廣告做好冷啟動。

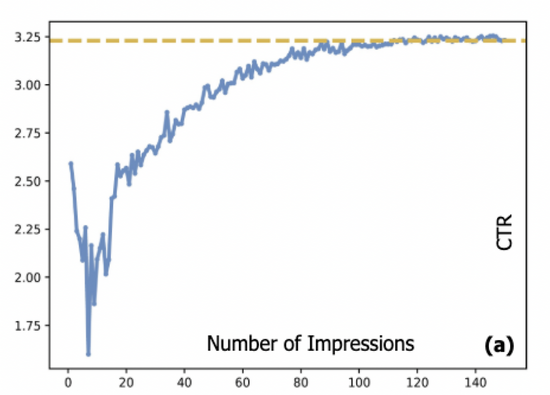
圖一：廣告CTR和展現(xiàn)次數(shù)之間的關(guān)系

探索和利用（E&E）算法通常被用來解決上述問題。在推薦或廣告系統(tǒng)中，常見的方法（如Contextual Multi-Armed Bandits，上下文多臂老虎機）一般會將該問題按照如下方式加以建模。在每步中，系統(tǒng)會基于策略P選擇一個操作（即為用戶推薦一個項目_ _）。為了最大化累積獎勵（通常使用總點擊量來衡量），系統(tǒng)需要權(quán)衡當前是偏重探索，還是偏重利用。先前的研究通常認為，高不確定性是潛在回報的衡量指標。一方面，策略P需要優(yōu)先選擇當前效用較大的項目以最大化本輪收益；另一方面，算法也需要選擇不確定度較大的操作以實現(xiàn)探索。如果用來表示權(quán)衡探索和利用的策略，那么系統(tǒng)對項目最終打分可以用如下公式表示：

不確定性估計已成為許多E&E算法的核心模塊。不確定性可能源于數(shù)據(jù)的可變性、測量噪聲和模型不穩(wěn)定性（例如：參數(shù)的隨機性），典型的估計方法包括蒙特卡洛MC-Dropout、貝葉斯神經(jīng)網(wǎng)絡、預測不確定性的高斯過程，以及基于梯度范數(shù)（模型權(quán)重）的不確定性建模等。在此基礎上，有兩種典型的探索策略：基于UCB的方法通常采用潛在回報的上限作為最終打分[1,2]，而基于湯普森采樣的方法是通過從估計的概率分布中抽樣來完成 [3]。

3. 方法介紹

我們認為，上述方法并未考慮一個完整的探索閉環(huán)。對于數(shù)據(jù)驅(qū)動的在線系統(tǒng)而言，探索的最終收益來自于從探索過程中獲取的反饋數(shù)據(jù)，以及反饋數(shù)據(jù)對于模型的訓練與更新。而模型預估的不確定度本身并不能完全反映整個反饋閉環(huán)。為此，我們引入了一個擬探索模塊，用于模擬完成探索動作后反饋數(shù)據(jù)對于模型的影響，并以此來衡量探索的有效性。分析發(fā)現(xiàn)，探索的有效性不僅取決于模型的預估不確定度，還取決于“對抗擾動”的大小。所謂對抗擾動，指的是在模型的輸入上加入的固定模長的擾動中使得模型輸出變化最大的擾動向量。在論文中，我們也證明了，模型利用被探索的數(shù)據(jù)進行一次訓練后，模型輸出變化的期望等價于在輸入向量中加入模長為不確定度、擾動向量為對抗梯度的增量向量。我們驗證了按照這種方式進行建模，可以閉環(huán)地估計出被探索樣本對模型的后續(xù)影響，從而估計出被探索樣本的真實價值。

我們將這種方法稱為 基于對抗梯度的探索（Adversarial Gradient driven Exploration） ，簡稱AGE。AGE模型由擬探索模塊（Pseudo-Exploration Module）與動態(tài)門控閾值單元（Dynamic Gating Unit）兩部分組成，其整體結(jié)構(gòu)如圖二所示。

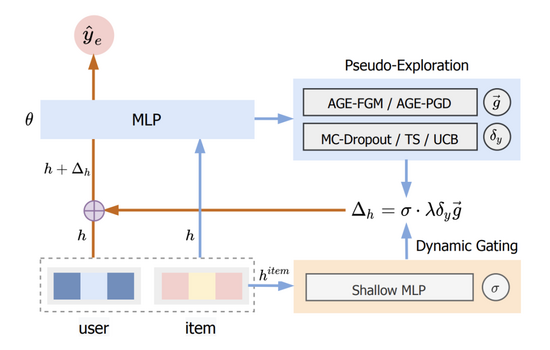
圖二：AGE結(jié)構(gòu)圖

其中部分的詳細介紹詳見3.1節(jié)，部分的詳見3.3節(jié)。

3.1 擬探索模塊（Pseudo-Exploration Module）

3.1.1 模塊簡介

擬探索模塊的主要目的是定量模擬模型使用探索樣本加以訓練后，對該樣本打分的變化，從而估計探索對于模型的閉環(huán)影響。經(jīng)過推導，我們發(fā)現(xiàn)可以通過公式(2)來完成上述過程，其中代表了探索后模型對該樣本的打分，我們將其用于最終的排序。

上式表示我們不需要對原有模型參數(shù)進行任何操作，只需要在輸入的表征中加上對抗梯度，預估不確定度以及手工設定的超參數(shù)的乘積，即可完成對探索后模型預估分的模擬。 其中參數(shù) 與 的計算方法，我們在下一節(jié)中介紹。本節(jié)后續(xù)我們將介紹擬探索模塊中公式(2)的詳細推導過程。

3.1.2 詳細推導

對于每條數(shù)據(jù)樣本而言，模型的訓練將會影響兩部分參數(shù)：該樣本對應的表征（包含商品、用戶embedding等）與模型參數(shù)。因為模型參數(shù)在訓練中的目標是適應所有樣本而不是單條樣本，所以我們可以認為訓練單條樣本主要會對樣本對應的表征產(chǎn)生影響，而模型參數(shù)本身只需要微小的調(diào)整。因此，在后續(xù)研究中，我們將忽略的調(diào)整，而僅關(guān)注樣本對應的表征的變化。假設包含表征的樣本真實label為，訓練時，我們需要尋找到的更新量，以最小化損失函數(shù)。基于此，我們定義：

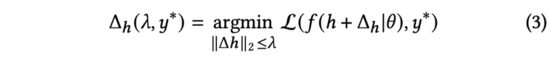
其中代表訓練中使用的損失函數(shù)，而在CTR預估任務中一般使用交叉熵損失函數(shù)。同時，我們用來約束表征的最大變化。為了簡化書寫，后續(xù)我們將上述公式右側(cè)寫為。

依據(jù)拉格朗日中值定理，在的二范數(shù)接近0的情況下，我們可以將上述損失函數(shù)公式(3)推導為：

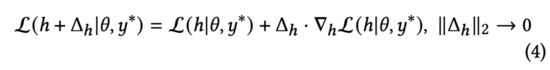
我們觀察公式(4)，易發(fā)現(xiàn)該損失函數(shù)在與兩個向量有相反的方向時，獲得最小值。在公式(3)中，我們約束對抗擾動。因此，通過求解公式(3)，我們得到：

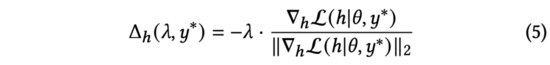
實踐中，我們用來替代公式(5)中的歸一化梯度。通過求導鏈式法則，可以展開為和兩部分。進一步計算，得到：

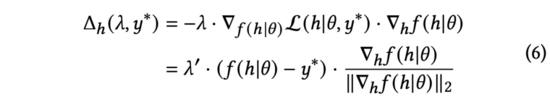
在上式中，我們將重新縮放到以保持等式的成立。盡管含義不同，但它們都是手動調(diào)節(jié)的超參數(shù)，故我們可以直接以完成替換。我們進一步簡化公式(6)為：

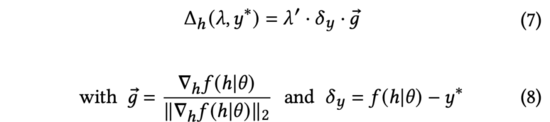
上式中，歸一化梯度表示模型輸出相對于輸入表征的導數(shù)方向。由于真實的用戶反饋在探索時無法得到，我們將使用預估不確定度來衡量預測得分與真實用戶反饋之間的差值。

公式(7)中，我們找到了在的約束下可以最大化改變模型預測輸出的解析解（推導與公式(3)到公式(5)相同）。進一步，我們也發(fā)現(xiàn)上述對輸入表征添加的過程與對抗擾動（見公式(9)）的形式相同。

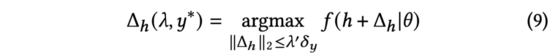
因此，我們利用對抗梯度來的替代公式(7)中的，并將我們的方法命名為基于對抗性梯度的探索算法。

公式(9)表明，AGE最有效的探索方式為給表征輸入加入對抗擾動，以擾動后模型的輸出結(jié)果為排序因子：以對抗梯度為輸入表征的擾動向量方向，以及以預測不確定性度的擾動力度。于是，在得到和后，我們可以用下述公式來計算探索后的模型預測分數(shù)，該公式即為前述公式(2)。

3.2 實現(xiàn)細節(jié)

在AGE中，我們采用MC-Dropout的方法估計不確定度。具體說來，MC-Dropout為深度模型中的每個神經(jīng)元賦予隨機Mask權(quán)重，具體做法如下公式(11)所示。該方法的一個好處是，我們可以在不改變模型原始結(jié)構(gòu)的基礎上直接獲取不確定性。在實際操作中，可以通過UCB的思想計算dropout的方差來表示不確定度，或者參考湯普森隨機采樣的方式通過計算采樣與均值的差異來計算不確定度，也即公式（12）和公式（13）。

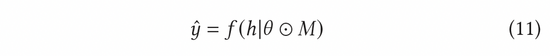
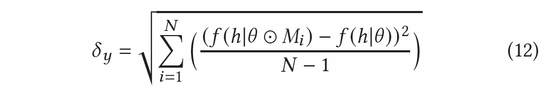
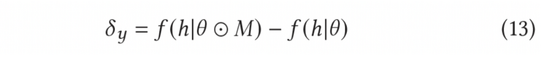
歸一化對抗梯度可以根據(jù)公式(8)中的快速梯度法（FGM）來計算獲得。為了更加精確地計算出對抗梯度，我們還可以進一步利用近端梯度下降（PGD）方法，多步迭代更新梯度，如公式（14）所示。

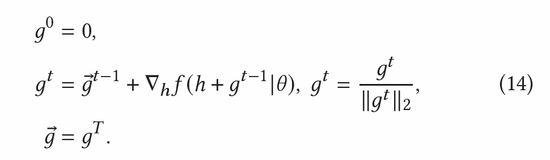
3.3 動態(tài)門控閾值單元（Dynamic Gating Unit）

在實踐中，我們發(fā)現(xiàn)并非所有廣告都值得探索。在一般的Top-K廣告系統(tǒng)中，能夠為最終用戶展現(xiàn)的廣告數(shù)量是相對較少。因此，本身點擊率低的廣告（比如廣告本身質(zhì)量較低），即使模型對這部分廣告的預估存在很高的不確定性，但考慮廣告系統(tǒng)的業(yè)務屬性，其探索價值仍然是很低的。雖然我們可以通過探索獲得了這些廣告的大量數(shù)據(jù)，使得這些廣告被模型充分訓練而估計的更加準確；但因為這些廣告的本身過低的點擊率會使得即使充分探索后，這些廣告依然無法自行獲取流量，這樣的探索無疑是低效的。在本文中，我們嘗試了一種簡單的啟發(fā)式方法來提高探索的效率——如果模型對該廣告的預估分數(shù)高于該廣告在所有人群中的平均點擊率，我們將進行探索；否則，探索將不會發(fā)生。

為了計算廣告的平均點擊率，我們引入了動態(tài)門控閾值單元（DGU）模塊。DGU僅使用廣告?zhèn)忍卣髯鳛檩斎雭眍A估廣告的平均點擊率。當模型的預估點擊率低于DGU模塊預估的廣告平均點擊率時，不予探索，反之則進行正常的探索。該過程如下式所示：

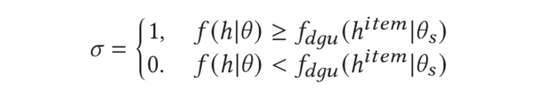
最終，我們將代入公式(10)中，獲得如下AGE探索模型最終完整的計算方式。

4. 實驗評測

4.1 離線實驗

我們對比了三大類基線方法，包括基于隨機采樣的探索方法，基于深度模型的探索方法，以及基于梯度的探索方法，結(jié)果如表1所示。觀察可得，基于湯普森采樣（TS）方法構(gòu)建的基線模型均優(yōu)于基于UCB的模型，證明TS是一種更好的衡量模型不確定度的算法。此外，我們可以觀察到AGE算法優(yōu)于所有的基線方法，這也證明了AGE方法的有效性。具體而言，AGE-TS和AGE-UCB的表現(xiàn)均優(yōu)于最好基線UR-gradient-TS和UR-gradient-UCB [4]，提升數(shù)值分別為5.41%和15.3%。而AGE-TS方法相比于不進行探索的基準方法提高了整整28.0%的點擊量。值得注意的是，基于AGE的UCB和TS算法AGE-UCB和AGE-TS取得了相似的效果，基于gradient的UCB和TS算法并非如此，這也證明了AGE可以彌補UCB方法的不穩(wěn)定性。

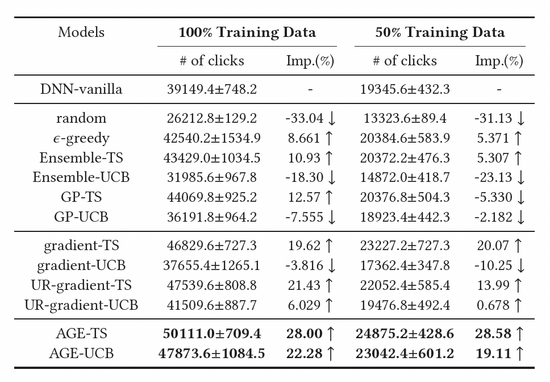
表1：離線實驗結(jié)果

我們也進行了大量的消融實驗來證明了各個模塊的有效性。如表2所示，閾值單元、對抗梯度、不確定度單元，三者均不可或缺。為了進一步確定DGU的效果，我們嘗試了不同的固定閾值參數(shù)，最后也發(fā)現(xiàn)其效果也不及DGU的動態(tài)閾值。

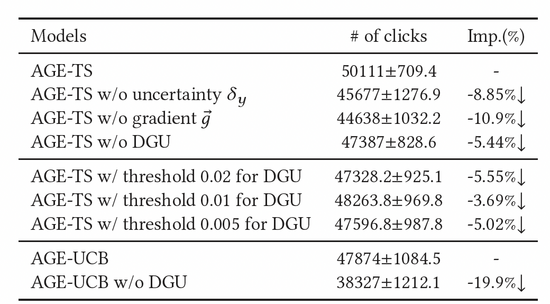
表2：消融實驗結(jié)果

4.2 在線實驗

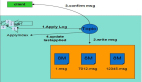
我們也將AGE模型部署到阿里媽媽展示廣告系統(tǒng)中，為了準確評估模型的探索價值，我們設計了基于公平桶的評測方法。如圖三所示，我們首先設置桶C和桶D用于收集數(shù)據(jù)。在桶D中，我們部署AGE等探索算法，而在桶C中，我們采用不做探索的常規(guī)CTR模型。經(jīng)過一段時間之后，我們將桶C和桶D獲取的反饋數(shù)據(jù)分別應用于公平桶A和B上部署模型的訓練。最終，我們將比較公平桶A和B上的模型效果。在線實驗中，我們使用幾個標準指標進行評估，包括點擊率CTR、被探索廣告的展現(xiàn)數(shù)量PV和預測CTR與真實CTR之比PCOC。此外，我們還引入了一個用于衡量廣告主的滿意度的業(yè)務指標（AFR）。

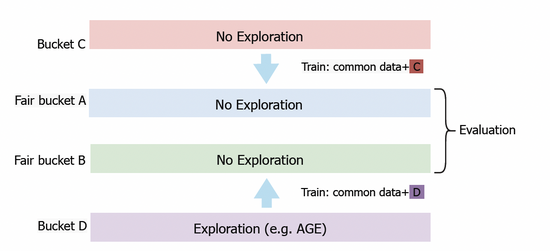
圖三：公平桶實驗方案

如表3所示，上述指標都得到了有效的提升。其中，AGE明顯優(yōu)于所有其他方法：CTR和PV分別比基線模型高6.4%和3.0%。同時AGE模型的使用還提升了模型的預測精度，即預估準度PCOC更接近1。更重要的是，AFR指標也有5.5%的提升，這表明我們的探索方法可以有效提升廣告主的體驗。

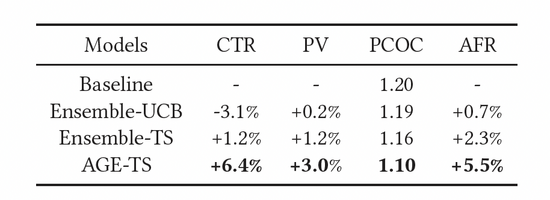
表3：在線實驗結(jié)果

5. 總結(jié)

與大多數(shù)專注于估計潛在回報的探索&利用方法不同，我們的方法AGE從在線學習的數(shù)據(jù)驅(qū)動的角度重新構(gòu)建了這一問題。除了可以估計當前模型預測的不確定度外，AGE算法借助擬探索模塊，更進一步地考慮探索樣本對模型訓練的后續(xù)影響。我們在學術(shù)研究數(shù)據(jù)集和生產(chǎn)鏈路上都進行了A/B測試實驗，相關(guān)結(jié)果均證實了AGE方法的有效性。今后我們會將AGE部署于更多的應用場景中。