技術(shù)面試不發(fā)愁!從幾個小技巧中探析數(shù)據(jù)結(jié)構(gòu)的樂趣
本文轉(zhuǎn)載自公眾號“讀芯術(shù)”(ID:AI_Discovery)
如果你即將要面臨大型科技公司的技術(shù)面試,那么數(shù)據(jù)結(jié)構(gòu)和算法技巧方面的問題一定不能忘記準(zhǔn)備。
本文就將介紹一些適合在面試使用的優(yōu)化代碼的小技巧。但在學(xué)習(xí)技巧之前,你得確保自己已經(jīng)了解了簡單的數(shù)據(jù)結(jié)構(gòu),比如樹、堆、圖和哈希映射。
注意,你要理解而不是僅僅記住它們。
技巧1:針對“第K個最小/最大元素”問題的最小/最大堆
問題:給定一個數(shù)字列表,使用堆數(shù)據(jù)結(jié)構(gòu)找到第三小的元素:
- [4,20,16,10,0,47,…]
當(dāng)以“查找列表中第K個最小元素”的形式提出問題時,由于問題語句中的“最小”一詞,自然會傾向于使用最小堆提出解決方案。這兒有一個簡單的解決方案:
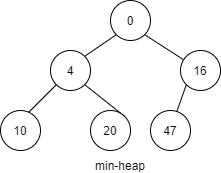
構(gòu)建給定列表的最小堆并調(diào)用extractMin() k次。這個解決方案的時間復(fù)雜度是O(n + kLogn),消耗了O(n)的額外內(nèi)存。
想要優(yōu)化內(nèi)存和時間復(fù)雜度,這兒有一個更好的解決方案:

- 從數(shù)組的前k個元素構(gòu)建最大堆
- 對于每個剩余的元素,將該元素與最大堆的根進行比較。如果它小于根,則用元素替換根并調(diào)用heapify()。
- 完成了第二步,堆的根將是第k個最小的元素。
時間復(fù)雜度:O(k +(n-k)Logk)
- 對于第K個最小的問題使用最大堆。
- 對于第K個最大的問題使用最小堆。
注意:對于這個問題有不同的解決方案,可以使用快速選擇算法、中位數(shù)等。選擇堆是因為它們更容易理解和可視化。
技巧2:使用索引映射
索引映射是在技術(shù)面試中多次使用的一種技術(shù),它以使用更多內(nèi)存為代價來節(jié)省搜索時間。
問題:用O(1)搜索時間實現(xiàn)最小堆數(shù)據(jù)結(jié)構(gòu)。
從簡單開始。只關(guān)注“搜索”部分,最小堆已經(jīng)實現(xiàn)了。

這是一個最小堆,它被表示為如下數(shù)組:
- [0, 4, 16, 10, 20, 47]
想找到給定節(jié)點的下標(biāo),比如說10。
對數(shù)組進行線性搜索,直到找到元素10,這將花費O(n)時間。但需要O(1)時間。也許是因為想要更新這個節(jié)點的值,正在執(zhí)行大量的更新,所以不想花時間去尋找元素。
很明顯,除非犧牲一些資源,否則不可能神奇地?fù)碛蠴(1)搜索時間。我們可以在哈希映射中保留每個節(jié)點的索引。無論何時更新堆,都需要更新這個散列映射上的索引。
對于上面的堆[0,4,16,10,20,47],索引映射為:
- {
- 0:0,
- 4:1,
- 16:2
- 10:3,
- 20:4
- 47:5
- }
現(xiàn)在我們可以求出節(jié)點10在O(1)時間內(nèi)的位置。如果更改堆中元素的順序,還將更新它們在索引映射數(shù)據(jù)結(jié)構(gòu)中的相對索引。
注意:可以使用其他的數(shù)據(jù)結(jié)構(gòu),例如索引映射的樹。
追問:能對指針/引用使用同樣的技術(shù)嗎?
技巧3:在O(1)時間內(nèi)從無序數(shù)組中刪除一個元素
問題:在O(1)時間內(nèi)移除[10,4,56,0,8,1]中的元素“4”。
從數(shù)組中刪除一個特定的元素時,所有后續(xù)的元素都向左移動,這將花費O(n)個時間。這很完美,而且是最常用的技術(shù),它保留了數(shù)組的順序。
但如果你不在意元素的順序,有一個更簡單的方法可以實現(xiàn)O(1)時間內(nèi)“刪除”:用數(shù)組的最后一個元素替換要刪除的元素。然后將數(shù)組大小減小1。
對于上面這個例子,刪除“4”就可以寫成:
- [10, 1, 56, 0, 8, 1] #用最后一個元素“1”替換“4”
- [10, 1, 56, 0, 8] #減少數(shù)組大小1。
追問:如果在意順序呢?可以將其保存在不同的數(shù)據(jù)結(jié)構(gòu)中嗎?
技巧4:了解二分查找的基本原理
二分查找不僅僅是為了在一個有序數(shù)組中找到一個元素,它有著更強大的力量。一旦理解了它的基本原理,就會被能用它解決的問題的能力所折服。
問題:
農(nóng)民約翰新建了一個有N個畜欄的倉房。給定一個大小為N的整數(shù)數(shù)組A,其中數(shù)組中的每個元素表示畜欄的位置,整數(shù)B表示奶牛的數(shù)量。他的奶牛不喜歡這個倉房的布局,這使它們在倉庫中變得很有攻擊性。為了防止奶牛互相傷害,約翰想把奶牛分配到畜欄里。
圖源:unsplash
約翰想使它們之間的最小距離盡可能大。那么這個最小距離的最大值是多少?我們能用二分查找法解決這個問題嗎?
當(dāng)然可以。閱讀這篇關(guān)于topcoder的文章,你將會明白該怎樣具體操作:
mailto:https://www.topcoder.com/community/competitive-programming/tutorials/binary-search
技巧5:位操作
位操作是優(yōu)化代碼(主要是內(nèi)存)的一種有用技術(shù),可以用于各種問題,你可以使用移位、和/或/異或/非操作。
以下是你必須了解的比特操作:
- x ^ x = 0
- x ^ 0 = x
- x | 0 = x
- x & 1 = xGet i th bit on num: (num & (1 << i)) != 0
- Set i th bit on num: num |= 1 << i
問題:給定一個整數(shù)數(shù)組,除了一個元素外,其他元素都出現(xiàn)兩次。找到這個元素。
- Sample input: [1, , 8, 1, 8]
- Output: 0
你當(dāng)然可以使用哈希表或其他技術(shù)來解決這個問題,但我有一個更簡單的方法。我們給到的是x ^ 0 =x和x ^ x =0。如果對數(shù)組的所有元素進行XOR操作,重復(fù)的元素會相互抵消(x ^ x = 0),最后,會得到不重復(fù)的元素:
- arr = [1, 0, 8, 1, 8]
- result = 0for num in arr:
- result ^= numreturn result
這將只花費O(n)時間和O(1)內(nèi)存。
圖源:unsplash
技巧的意義體現(xiàn)在實際操作之中,快去試試用它們解答面試問題吧,你會大有收獲的。