面試官:換人!他連動態(tài)規(guī)劃的一個(gè)模型三個(gè)特征都不懂
前言
之前我們簡單總結(jié)了一下動態(tài)規(guī)劃的解題套路,不少人反饋受益頗豐(如果是動態(tài)規(guī)劃初學(xué)者,強(qiáng)烈建議看看!)不過有位讀者說雖然動態(tài)規(guī)劃的解題套路是看懂了,不過一些動態(tài)規(guī)劃的主要特征,如無后效性沒有提到,所以今天我們就簡單以一道題再來溫習(xí)一下動態(tài)規(guī)劃的解題套路及其主要特征。
什么樣的問題適合用動態(tài)規(guī)劃實(shí)現(xiàn)呢,我們在一文學(xué)會動態(tài)規(guī)劃解題技巧中曾經(jīng)提到,只要問題符合「遞歸+重復(fù)」,則基本斷定可以用動態(tài)規(guī)劃來解題。簡單來說能用動態(tài)規(guī)劃解決的問題符合「一個(gè)模型三個(gè)特征」
一個(gè)模型: 多階段決策最優(yōu)解模型,多階段意味著問題可以分解為多個(gè)階段進(jìn)行求解,每個(gè)階段通常都有一個(gè)最優(yōu)解,每個(gè)階段的最優(yōu)解通過遞推公式可以求得下個(gè)階段的最優(yōu)解,求得了每個(gè)階段的最優(yōu)解,自然而然全局最優(yōu)解也就解決了
三個(gè)特征
- 最優(yōu)子結(jié)構(gòu):上文一個(gè)模型中所述每個(gè)階段的最優(yōu)解即最優(yōu)子結(jié)構(gòu)
- 無后效性:當(dāng)前階段的最優(yōu)解只與它上個(gè)階段的最優(yōu)解有關(guān),它不 Care 上個(gè)階段的最優(yōu)解是怎么得來的,之后階段的決策(最優(yōu)解)也不會影響之前階段問題的求解
- 重復(fù)子問題: 如果問題采用自頂向下的方式解決,通常都會有重復(fù)子問題的,即我們所說的「遞歸+重復(fù)」,此時(shí)我們可以采用自下而上的套路來求解問題
如果大家對上文中的「一個(gè)模型三個(gè)特征」沒感覺也沒關(guān)系,我們可以套用如下動態(tài)規(guī)劃解題模板
- 判斷是否可用遞歸來解,可以的話進(jìn)入步驟 2
- 分析在遞歸的過程中是否存在大量的重復(fù)子問題
- 采用備忘錄的方式來存子問題的解以避免大量的重復(fù)計(jì)算(剪枝)
- 改用自底向上的方式來遞推,即動態(tài)規(guī)劃
接下來我們先通過一道比較有意思的習(xí)題來套用以上解題模板來解題,然后再來解釋一下動態(tài)規(guī)劃的「一個(gè)模型三個(gè)特征」
問題定義
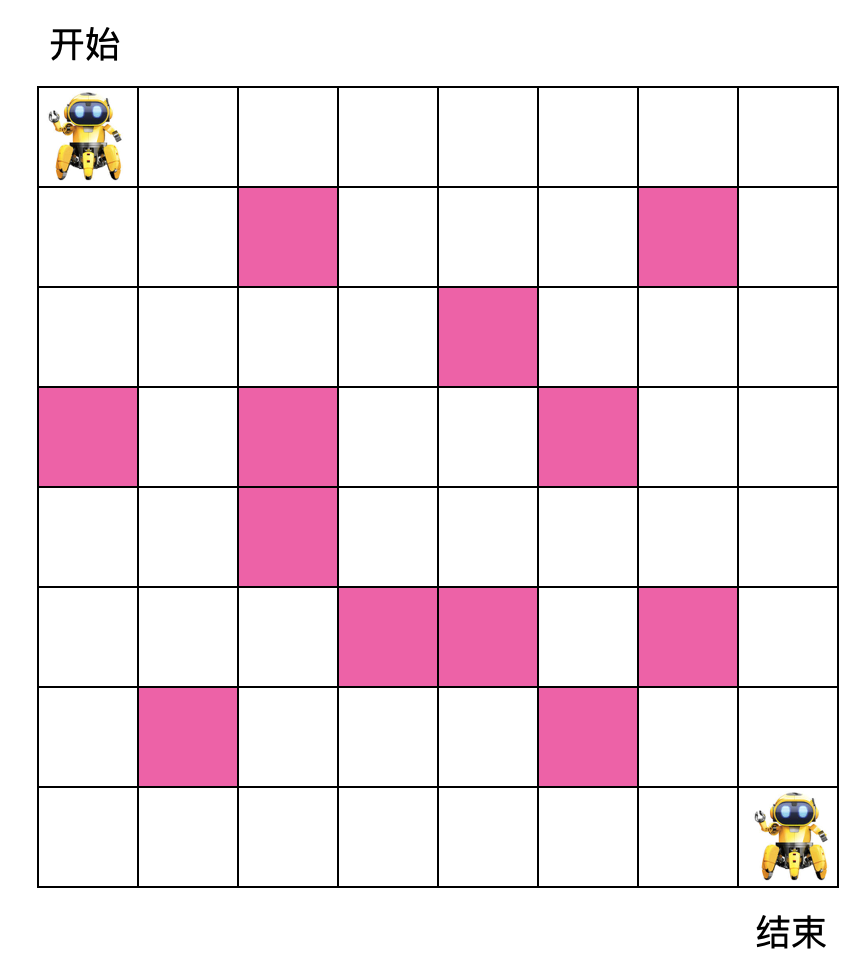
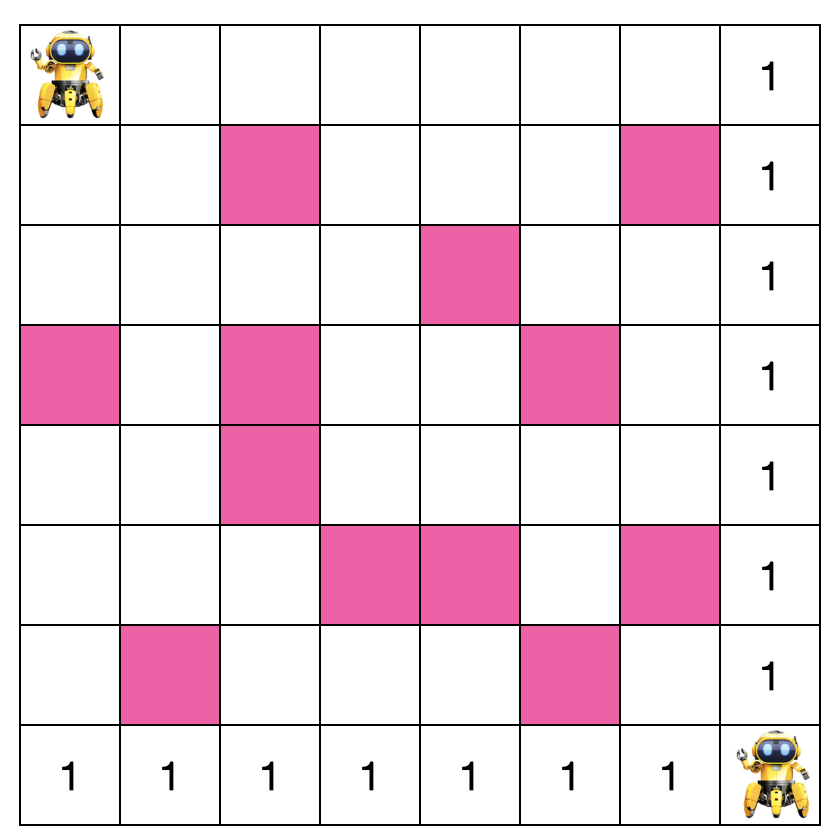
有如下 8 x 8 格子,機(jī)器人需要從開始位置走到結(jié)束位置,每次只能朝右或朝下走,粉色格子為障礙物,機(jī)器人不能穿過,問機(jī)器人從開始位置走到結(jié)束位置最多共有多少種走法?
這題如果用動態(tài)規(guī)劃可能一時(shí)半會兒看不出來,那我們就用窮舉法來看看怎么解,所謂窮舉法就是把機(jī)器人所有的路徑全部算出來,然后再相加
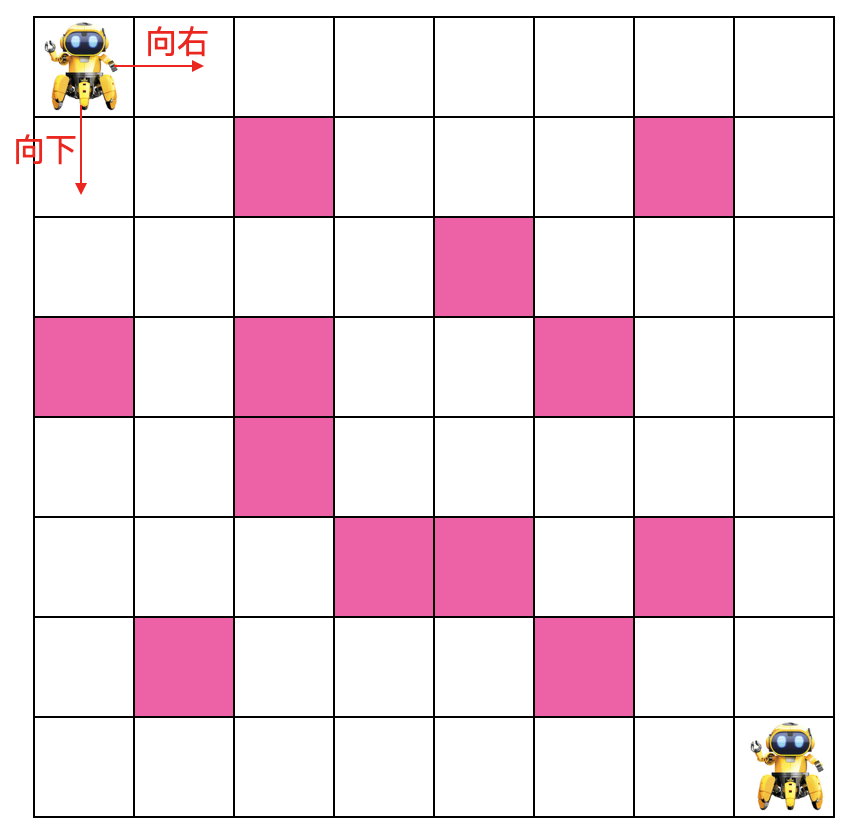
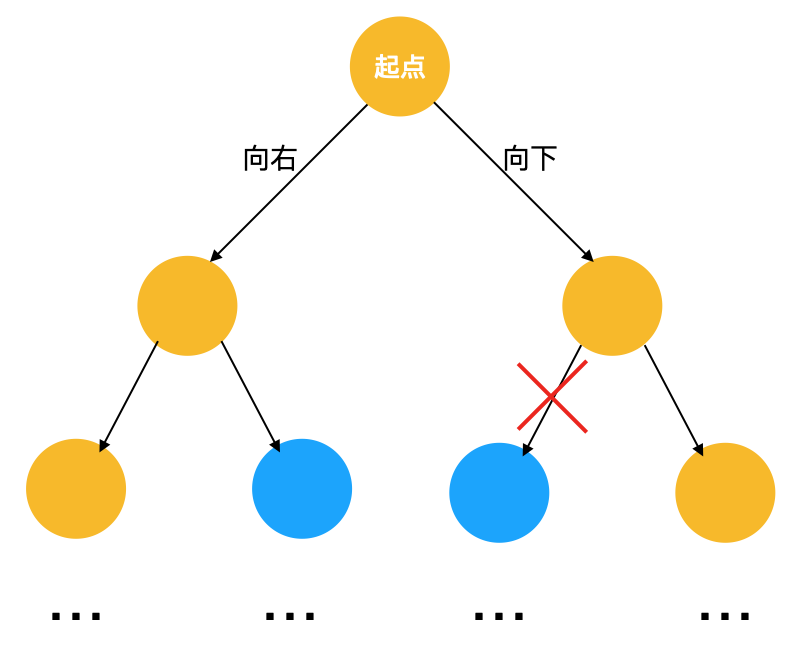
用窮舉法怎么做呢,對于機(jī)器人起始位置來說,它可以選擇向下或向右,所以它到終點(diǎn)的路徑數(shù)為其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)之和,偽代碼如下
- paths(start, end) = paths(start下方格子, end) + paths(start右邊格子, end)
對于每個(gè)格子來說,它也可以選擇向左或向右,由于可以得出對于每個(gè)選中的格子,它都符合以下遞推公式:
- paths(機(jī)器人所在格子, end) = paths(機(jī)器人所在格子下方格子, end) + paths(機(jī)器人所在格子右方格子, end)
表示成代碼如下:
- private int countPaths(boolean[][] grid, int row, int col) {
- if(isObstacle(grid, row, col)) return 0;
- if (isAtEnd(grid, row, col)) return 1;
- return countPaths(grid, row+1, col) + countPath(grid, row, col+1)
- }
看出規(guī)律了嗎,這其實(shí)是一個(gè)遞歸,那么如果用遞歸會有什么問題呢?
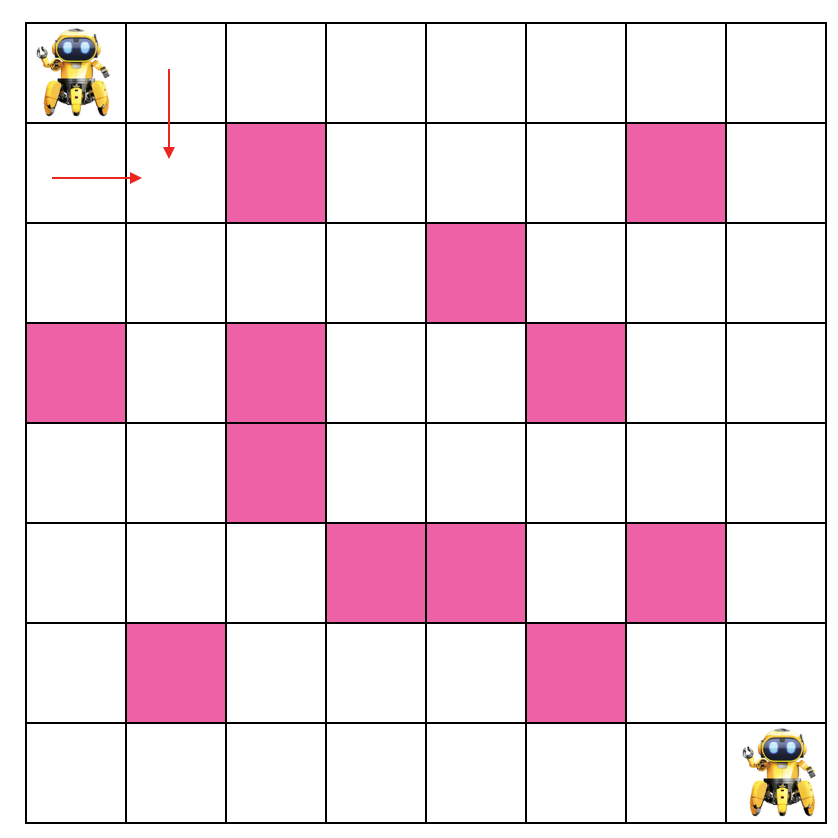
以上圖起始點(diǎn)出發(fā)為例,如果選擇了向右或向下,則右或下格子也可以選擇向右或向下,如果右格子選擇向下,下格子選擇向右,則這兩條路徑都經(jīng)過了相同的格子,這兩條路徑相交了!也就是出現(xiàn)了重復(fù)子問題!
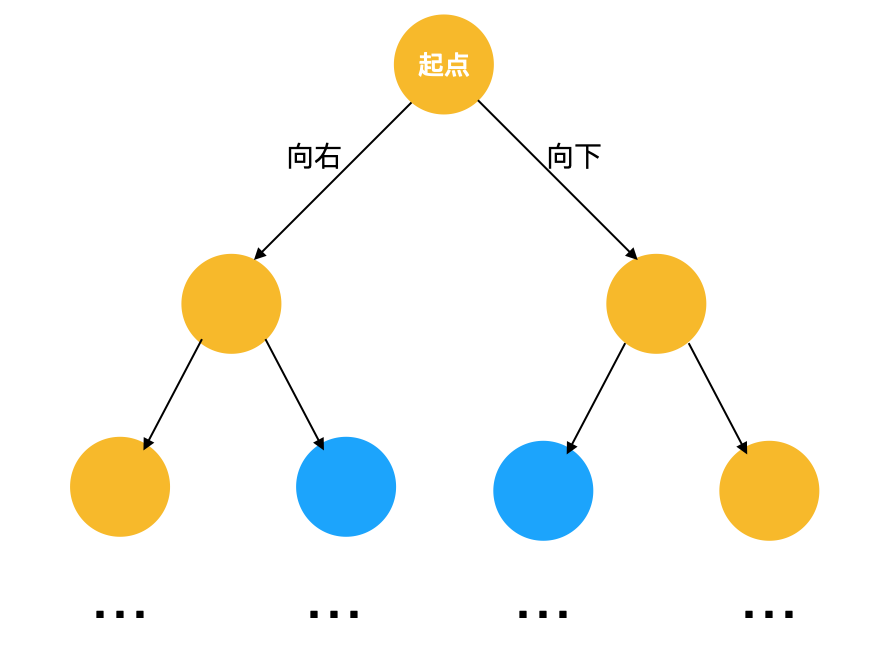
每次機(jī)器人可以選擇向右或向下走,如果我們把它抽象成一顆二叉樹,則結(jié)構(gòu)如下 :
注:藍(lán)色代表相同的方塊
由于是一顆二叉樹,時(shí)間復(fù)雜度顯然是 O(2^n),指數(shù)級別!原因當(dāng)然是由于解題中存在大量的重復(fù)子問題(圖中藍(lán)色代表相同方塊,即重復(fù)子問題),為了減少重復(fù)子問題,我們需要用備忘錄來保存中間的結(jié)果 (即減枝),這樣能讓時(shí)間復(fù)雜度大幅度減少,如下
經(jīng)過「遞歸+備忘錄」后其實(shí)時(shí)間復(fù)雜度和動態(tài)規(guī)劃已經(jīng)差不多了,不過我們之前一直強(qiáng)調(diào)盡量不要用遞歸的方式解題,因?yàn)檫f歸層級過深,很可能導(dǎo)致棧溢出。
所以接下來我們改用動態(tài)規(guī)劃的方式看看該如何解決。
遞歸是采用自頂向下的方式來解決問題,對應(yīng)到本題,就是從起點(diǎn)出發(fā),推導(dǎo)出到終點(diǎn)的所有路徑和,而動態(tài)規(guī)劃則是自下而上,即從終點(diǎn)出發(fā)推導(dǎo)出到起點(diǎn)的所有路徑和。對于最右邊和最底邊的格子來說,由于它們只能向下或向右走,所以分別在它們的位置上標(biāo) 1,代表從這些格子出發(fā)只有一種路徑,如下圖示:
最右和最下邊的格子的路徑數(shù)都填上了,其它格子就簡單了,顯然對于其它格子來說,
- paths(格子, end) = paths(下邊的格子, end) + paths(右邊的格子, end)
注:如果格子為障礙物,則其到終點(diǎn)的路徑數(shù)為 0
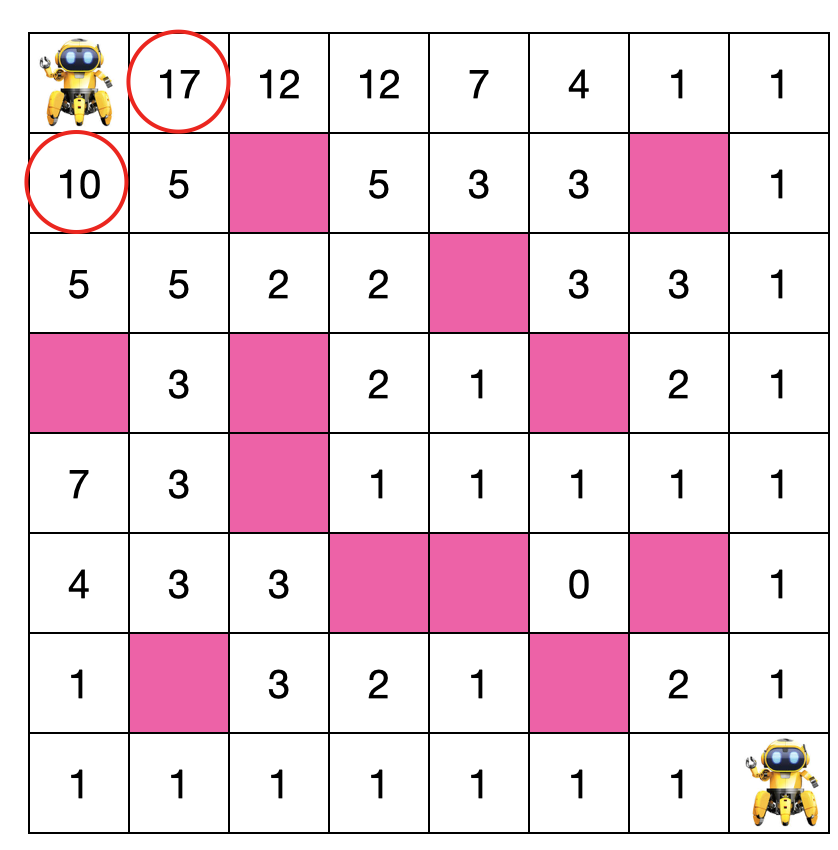
也就是說每個(gè)格子到終點(diǎn)的路徑和等于其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)之和,這樣從右到左,從下到上根據(jù)以上遞推公式依次填上每個(gè)格子的路徑數(shù)即可,如下
顯然從起點(diǎn)到終點(diǎn)的路徑和為 10 + 17 = 27。時(shí)間復(fù)雜度是多少呢,從下到上,從右到左,兩層循環(huán),顯然是 O(n^2),比起最開始用遞歸的 O(2^n) 大幅度提升了。
知道解題思路,用代碼實(shí)現(xiàn)相信不是什么大問題,我們以一個(gè)二維數(shù)組 grid[row][column] 來表示圖中的格子, 如果格子為障礙物,則其元素值初始化為 -1,其它格子元素初始化為 0,這樣我們只要做個(gè)兩層循環(huán)即可求得最終的解,代碼如下,注釋很詳盡,相信大家應(yīng)該能看懂
- public class Solution {
- /**
- * 初始化格子, -1 代表格子為障礙物
- */
- private static final int GRIDS[][] = {
- {0,0,0,0,0,0,0,0},
- {0,0,-1,0,0,0,-1,0},
- {0,0,0,0,-1,0,0,0},
- {-1,0,-1,0,0,-1,0,0},
- {0,0,-1,0,0,0,0,0},
- {0,0,0,-1,-1,0,-1,0},
- {0,-1,0,0,0,-1,0,0},
- {0,0,0,0,0,0,0,0}
- };
- static private int sumOfPaths() {
- // 格子為 8 x 8
- int N = 8;
- /**
- * 初始化最右邊的格子
- */
- for (int j = 0; j < N; j++) {
- GRIDS[N-1][j] = 1;
- }
- /**
- * 初始化最底部的格子
- */
- for (int i = 0; i < N; i++) {
- GRIDS[i][N-1] = 1;
- }
- /**
- * 從右到左,從下到上填滿每個(gè)格子的值,由于最右和最底部的格子都初始化了,
- * 所以從倒數(shù)第二行,倒數(shù)第二列開始遍歷
- */
- for (int i = N - 2; i >= 0; i--) {
- for (int j = N - 2; j >= 0; j--) {
- // 說明是障礙物,無需計(jì)算
- if (GRIDS[i][j] == -1) {
- continue;
- }
- /**
- * 每個(gè)要計(jì)算的格子到終點(diǎn)的路徑和等于其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)之和
- * 如果右邊或下邊的格子為障礙物,則其到終點(diǎn)的路徑數(shù)設(shè)置為 0
- */
- int rightPath = GRIDS[i+1][j] == -1 ? 0 : GRIDS[i+1][j];
- int bottomPath = GRIDS[i][j+1] == -1 ? 0 : GRIDS[i][j+1];
- GRIDS[i][j] = rightPath + bottomPath;
- }
- }
- /**
- * 遍歷完之后起點(diǎn)格子對應(yīng)的值即為最終所求的解
- */
- return GRIDS[0][0];
- }
- public static void main(String[] args) {
- int result = Solution.sumOfPaths();
- System.out.println("result = " + result);
- }
- }
可以看到,采用自底向上的動態(tài)規(guī)劃解法整體思路還是比較清晰且高效的。
問題解決了,現(xiàn)在我們回頭來看下動態(tài)規(guī)劃的一個(gè)模型和三個(gè)特征該如何理解
一個(gè)模型: 即多階段決策最優(yōu)解模型,首先來看多階段,起始位置走向終點(diǎn),第一階段可以看作是從起點(diǎn)向右或向下走,第一階段選中格子后,第二階段就要從第一階段選中的格子往右或往下走。。。,可以看到它的問題解確實(shí)是由多階段的最優(yōu)組成的。
三個(gè)特征
1、最優(yōu)子結(jié)構(gòu)
上文我們說對于每個(gè)格子,它到終點(diǎn)的路徑數(shù)為其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)之和
- paths(格子, end) = paths(下邊的格子, end) + paths(右邊的格子, end)
即對于每個(gè)格子來說,只要算出它的最優(yōu)子結(jié)構(gòu)(其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)),則此格子到終點(diǎn)的路徑和得出的就是最優(yōu)解,進(jìn)而可知上文中計(jì)算的 GRID[0][0] 也是全局最優(yōu)解。
2、無后效性
每個(gè)格子到終點(diǎn)的路徑數(shù)只與其右邊格子到終點(diǎn)的路徑數(shù)與其下邊格子到終點(diǎn)的路徑數(shù)有關(guān),它不 care 這兩者的路徑數(shù)是怎么得出的,也就是當(dāng)前階段的解只與它上一層階段的解有關(guān),它并不關(guān)心這些解是怎么算出來的,同時(shí)當(dāng)前階段的解算完后,它并不會對之前的階段的解產(chǎn)生影響,這就是無后效性的含義。
3、 重復(fù)子問題
如果用遞歸的方式來做,我們之前分析過了,顯然存在重復(fù)子問題。
綜上,此題符合動態(tài)規(guī)劃的「一個(gè)模型三個(gè)特征」,所以可以用動態(tài)規(guī)劃來解題
總結(jié)本文用一道比較常見的習(xí)題來幫助大家重新溫習(xí)了一下動態(tài)規(guī)劃的特點(diǎn):一個(gè)模型三個(gè)特征,相信大家對這些概念應(yīng)該有比較深刻的認(rèn)識了,其實(shí)忘記這些概念,使用前文所述動態(tài)規(guī)劃解題四步曲基本可以套路大多數(shù)動態(tài)規(guī)劃的問題,不過了解這些概念能進(jìn)一步地加深我們對動態(tài)規(guī)劃的理想,知其然,知其所以然也很重要。
本文轉(zhuǎn)載自微信公眾號「碼海」,可以通過以下二維碼關(guān)注。轉(zhuǎn)載本文請聯(lián)系碼海公眾號。