什么叫回溯算法

對于回溯算法的定義，百度百科上是這樣描述的：回溯算法實際上一個類似枚舉的搜索嘗試過程，主要是在搜索嘗試過程中尋找問題的解，當發現已不滿足求解條件時，就“回溯”返回，嘗試別的路徑。回溯法是一種選優搜索法，按選優條件向前搜索，以達到目標。但當探索到某一步時，發現原先選擇并不優或達不到目標，就退回一步重新選擇，這種走不通就退回再走的技術為回溯法，而滿足回溯條件的某個狀態的點稱為“回溯點”。許多復雜的，規模較大的問題都可以使用回溯法，有“通用解題方法”的美稱。

看明白沒，回溯算法其實就是一個不斷探索嘗試的過程，探索成功了也就成功了，探索失敗了就在退一步，繼續嘗試……，

組合總和

組合總和算是一道比較經典的回溯算法題，其中有一道題是這樣的。

找出所有相加之和為 n 的 k 個數的組合。組合中只允許含有 1 - 9 的正整數，并且每種組合中不存在重復的數字。

說明：

• 所有數字都是正整數。
• 解集不能包含重復的組合。

示例 1:

• 輸入: k = 3, n = 7
• 輸出: [[1,2,4]]

示例 2:

• 輸入: k = 3, n = 9
• 輸出: [[1,2,6], [1,3,5], [2,3,4]]

這題說的很明白，就是從1-9中選出k個數字，他們的和等于n，并且這k個數字不能有重復的。所以第一次選擇的時候可以從這9個數字中任選一個，沿著這個分支走下去，第二次選擇的時候還可以從這9個數字中任選一個，但因為不能有重復的，所以要排除第一次選擇的，第二次選擇的時候只能從剩下的8個數字中選一個……。這個選擇的過程就比較明朗了，我們可以把它看做一棵9叉樹，除葉子結點外每個節點都有9個子節點，也就是下面這樣

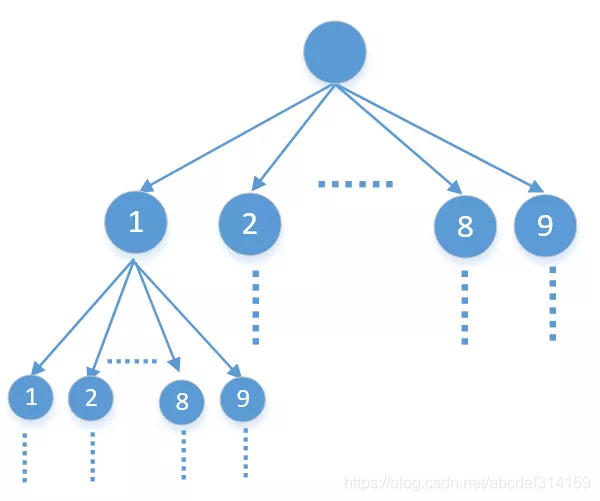
從9個數字中任選一個，就是沿著他的任一個分支一直走下去，其實就是DFS(如果不懂DFS的可以看下373，數據結構-6,樹)，二叉樹的DFS代碼是下面這樣的

public static void treeDFS(TreeNode root) { 
    if (root == null) 
        return; 
    System.out.println(root.val); 
    treeDFS(root.left);    treeDFS(root.right);} 

這里可以仿照二叉樹的DFS來寫一下9叉樹，9叉樹的DFS就是通過遞歸遍歷他的9個子節點，代碼如下

public static void treeDFS(TreeNode root) { 
    //遞歸必須要有終止條件 
    if (root == null) 
        return; 
    System.out.println(root.val);    //通過循環，分別遍歷9個子樹 
    for (int i = 1; i <= 9; i++) { 
        //2，一些操作，可有可無，視情況而定 
        treeDFS("第i個子節點"); 
        //3，一些操作，可有可無，視情況而定 
    }} 

DFS其實就相當于遍歷他的所有分支，就是列出他所有的可能結果，只要判斷結果等于n就是我們要找的，那么這棵9叉樹最多有多少層呢，因為有k個數字，所以最多只能有k層。來看下代碼

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //終止條件，如果滿足這個條件，再往下找也沒什么意義了 
    if (list.size() == k || n <= 0) { 
        //如果找到一組合適的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通過循環，分別遍歷9個子樹 
    for (int i = start; i <= 9; i++) { 
        //選擇當前值 
        list.add(i); 
        //遞歸 
        dfs(res, list, k, i + 1, n - i); 
        //撤銷選擇 
        list.remove(list.size() - 1); 
    } 
} 

代碼相對來說還是比較簡單的，我們來分析下(如果看懂了可以直接跳過)。

1. 代碼dfs中最開始的地方是終止條件的判斷，之前在426，什么是遞歸，通過這篇文章，讓你徹底搞懂遞歸中講過，遞歸必須要有終止條件。
2. 下面的for循環分別遍歷他的9個子節點，注意這里的i是從start開始的，所以有可能還沒有9個子樹，前面說過，如果從9個數字中選擇一個之后，第2次就只能從剩下的8個選擇了，第3次就只能從剩下的7個中選擇了……
3. 在第20行dsf中的start是i+1，這里要說一下為什么是i+1。比如我選擇了3，下次就應該從4開始選擇，如果不加1，下次還從3開始就出現了數字重復，明顯與題中的要求不符
4. for循環的i為什么不能每次都從1開始，如果每次都從1開始就會出現結果重復，比如選擇了[1，2]，下次可能就會選擇[2，1]。
5. 如果對回溯算法不懂的，可能最不容易理解的就是最后一行，為什么要撤銷選擇。如果經常看我公眾號的同學可能知道，也就是我經常提到的分支污染問題，因為list是引用傳遞，當從一個分支跳到另一個分支的時候，如果不把前一個分支的數據給移除掉，那么list就會把前一個分支的數據帶到下一個分支去，造成結果錯誤(下面會講)。那么除了把前一個分支的數據給移除以外還有一種方式就是每個分支都創建一個list，這樣每個分支都是一個新的list，都不互相干擾，也就是下面圖中這樣

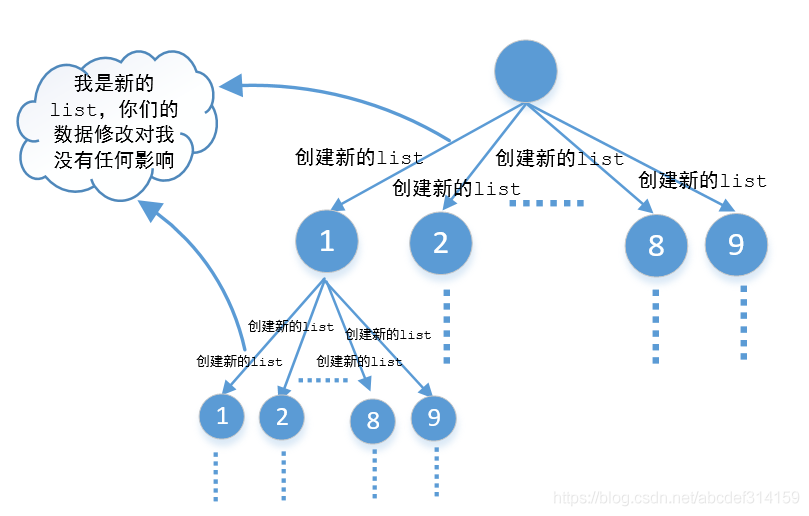
代碼如下

public List<List<Integer>> combinationSum3(int k, int n) { 
    List<List<Integer>> res = new ArrayList<>(); 
    dfs(res, new ArrayList<>(), k, 1, n); 
    return res; 
}private void dfs(List<List<Integer>> res, List<Integer> list, int k, int start, int n) { 
    //終止條件，如果滿足這個條件，再往下找也沒什么意義了 
    if (list.size() == k || n <= 0) { 
        //如果找到一組合適的就把他加入到集合list中 
        if (list.size() == k && n == 0) 
            res.add(new ArrayList<>(list)); 
        return; 
    } 
    //通過循環，分別遍歷9個子樹 
    for (int i = start; i <= 9; i++) { 
        //創建一個新的list，和原來的list撇清關系，對當前list的修改并不會影響到之前的list 
        List<Integer> subList = new LinkedList<>(list); 
        subList.add(i); 
        //遞歸 
        dfs(res, subList, k, i + 1, n - i); 
        //注意這里沒有撤銷的操作，因為是在一個新的list中的修改，原來的list并沒有修改， 
        //所以不需要撤銷操作 
    } 
} 

我們看到最后并沒有撤銷的操作，這是因為每個分支都是一個新的list，你對當前分支的修改并不會影響到其他分支，所以并不需要撤銷操作。

注意：大家盡量不要寫這樣的代碼，這種方式雖然也能解決，但每個分支都會重新創建list，效率很差。

要搞懂最后一行代碼首先要明白什么是遞歸，遞歸分為遞和歸兩部分，遞就是往下傳遞，歸就是往回走。遞歸你從什么地方調用最終還會回到什么地方去，我們來畫個簡單的圖看一下

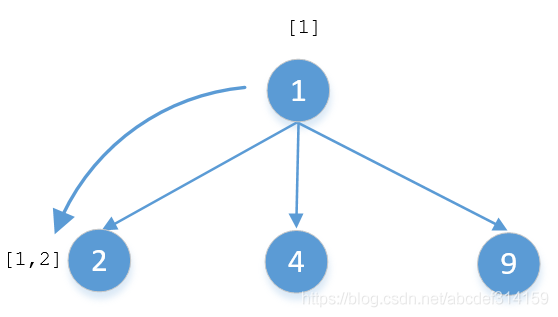
這是一棵非常簡單的3叉樹，假如要對他進行DFS遍歷，當沿著1→2這條路徑走下去的時候，list中應該是[1，2]。因為是遞歸調用最終還會回到節點1，如果不把2給移除掉，當沿著1→4這個分支走下去的時候就變成[1，2，4]，但實際上1→4這個分支的結果應該是[1，4]，這是因為我們把前一個分支的值給帶過來了。當1，2這兩個節點遍歷完之后最終還是返回節點1，在回到節點1的時候就應該把結點2的值給移除掉，讓list變為[1]，然后再沿著1→4這個分支走下去，結果就是[1，4]。

我們來總結一下回溯算法的代碼模板吧

private void backtrack("原始參數") { 
    //終止條件(遞歸必須要有終止條件) 
    if ("終止條件") { 
        //一些邏輯操作（可有可無，視情況而定） 
        return; 
    }    for (int i = "for循環開始的參數"; i < "for循環結束的參數"; i++) { 
        //一些邏輯操作（可有可無，視情況而定） 
        //做出選擇 
        //遞歸 
        backtrack("新的參數"); 
        //一些邏輯操作（可有可無，視情況而定） 
        //撤銷選擇 
    } 
} 

有了模板，回溯算法的代碼就非常容易寫了，下面就根據模板來寫幾個經典回溯案例的答案。

八皇后問題

八皇后問題也是一道非常經典的回溯算法題，前面也有對八皇后問題的專門介紹，有不明白的可以先看下394，經典的八皇后問題和N皇后問題。他就是不斷的嘗試，如果當前位置能放皇后就放，一直到最后一行如果也能放就表示成功了，如果某一個位置不能放，就回到上一步重新嘗試。比如我們先在第1行第1列放一個皇后，如下圖所示

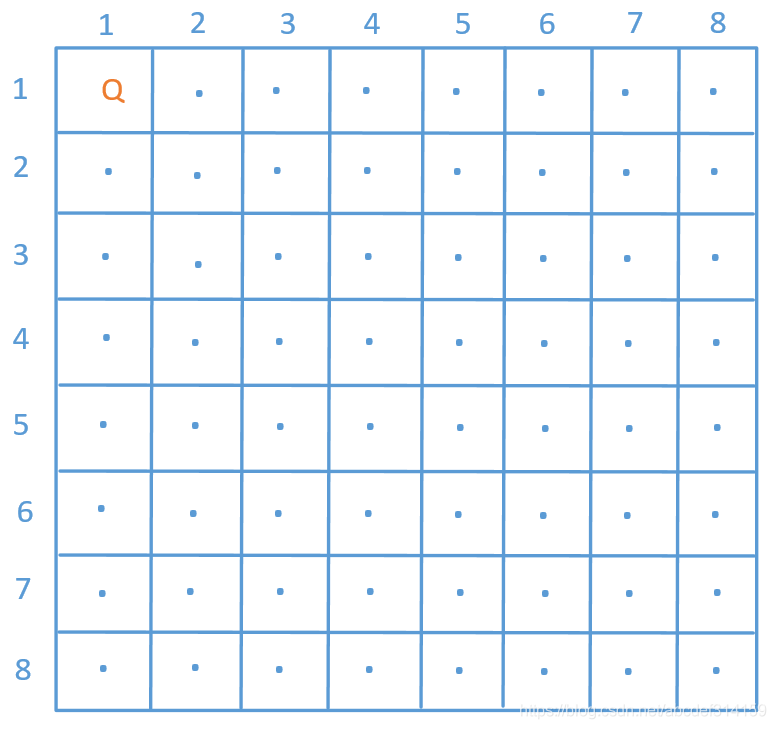
然后第2行從第1列開始在不沖突的位置再放一個皇后，然后第3行……一直這樣放下去，如果能放到第8行還不沖突說明成功了，如果沒到第8行的時候出現了沖突就回到上一步繼續查找合適的位置……來看下代碼

//row表示的是第幾行 
public void solve(char[][] chess, int row) { 
    //終止條件，row是從0開始的，最后一行都可以放，說明成功了    if (row == chess.length) {        //自己寫的一個公共方法，打印二維數組的，        //主要用于測試數據用的        Util.printTwoCharArrays(chess);        System.out.println();        return;    }    for (int col = 0; col < chess.length; col++) { 
        //驗證當前位置是否可以放皇后 
        if (valid(chess, row, col)) { 
            //如果在當前位置放一個皇后不沖突， 
            //就在當前位置放一個皇后 
            chess[row][col] = 'Q'; 
            //遞歸，在下一行繼續…… 
            solve(chess, row + 1); 
            //撤銷當前位置的皇后 
            chess[row][col] = '.'; 
        } 
    } 
} 

全排列問題

給定一個沒有重復數字的序列，返回其所有可能的全排列。

• 示例:
• 輸入: [1,2,3]
• 輸出:

[  
[1,2,3],  
[1,3,2],  
[2,1,3],  
[2,3,1],  
[3,1,2],  
[3,2,1]  
] 

這道題我們可以把它當做一棵3叉樹，所以每一步都會有3種選擇，具體過程就不在分析了，直接根據上面的模板來寫下代碼

public List<List<Integer>> permute(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    backtrack(list, new ArrayList<>(), nums); 
    return list; 
}private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums) { 
    //終止條件 
    if (tempList.size() == nums.length) { 
        //說明找到一一組組合 
        list.add(new ArrayList<>(tempList)); 
        return; 
    } 
    for (int i = 0; i < nums.length; i++) { 
        //因為不能有重復的，所以有重復的就不能選 
        if (tempList.contains(nums[i])) 
            continue; 
        //選擇當前值 
        tempList.add(nums[i]); 
        //遞歸 
        backtrack(list, tempList, nums); 
        //撤銷選擇 
        tempList.remove(tempList.size() - 1); 
    } 
} 

是不是感覺很簡單。

子集問題

給定一組不含重復元素的整數數組 nums，返回該數組所有可能的子集(冪集)。

• 說明：解集不能包含重復的子集。
• 示例:
• 輸入: nums = [1,2,3]
• 輸出:

輸入: nums = [1,2,3] 
輸出: 
[ 
[3], 
[1], 
[2], 
[1,2,3], 
[1,3], 
[2,3], 
[1,2], 
[] 
] 

我們還是根據模板來修改吧

public List<List<Integer>> subsets(int[] nums) { 
    List<List<Integer>> list = new ArrayList<>(); 
    //先排序 
    Arrays.sort(nums); 
    backtrack(list, new ArrayList<>(), nums, 0); 
    return list; 
} 
private void backtrack(List<List<Integer>> list, List<Integer> tempList, int[] nums, int start) { 
    //注意這里沒有寫終止條件，不是說遞歸一定要有終止條件的嗎，這里怎么沒寫，其實這里的終止條件 
    //隱含在for循環中了，當然我們也可以寫if(start>nums.length) rerurn;只不過這里省略了。 
    list.add(new ArrayList<>(tempList)); 
    for (int i = start; i < nums.length; i++) { 
        //做出選擇 
        tempList.add(nums[i]); 
        //遞歸 
        backtrack(list, tempList, nums, i + 1); 
        //撤銷選擇 
        tempList.remove(tempList.size() - 1); 
    } 
} 

所以類似這種題基本上也就是這個套路，就是先做出選擇，然后遞歸，最后再撤銷選擇。在講第一道示例的時候提到過撤銷的原因是防止把前一個分支的結果帶到下一個分支造成結果錯誤。不過他們不同的是，一個是終止條件的判斷，還一個就是for循環的起始值，這些都要具體問題具體分析。下面再來看最后一到題解數獨。

解數獨

數獨大家都玩過吧，他的規則是這樣的

一個數獨的解法需遵循如下規則：

• 數字 1-9 在每一行只能出現一次。
• 數字 1-9 在每一列只能出現一次。
• 數字 1-9 在每一個以粗實線分隔的 3x3 宮內只能出現一次。

過程就不在分析了，直接看代碼，代碼中也有詳細的注釋，這篇講的是回溯算法，這里主要看一下backTrace方法即可，其他的可以先不用看

//回溯算法 
public static boolean solveSudoku(char[][] board) { 
    return backTrace(board, 0, 0); 
}//注意這里的參數，row表示第幾行，col表示第幾列。private static boolean backTrace(char[][] board, int row, int col) { 
    //注意row是從0開始的，當row等于board.length的時候表示數獨的 
    //最后一行全部讀遍歷完了，說明數獨中的值是有效的，直接返回true 
    if (row == board.length) 
        return true; 
    //如果當前行的最后一列也遍歷完了，就從下一行的第一列開始。這里的遍歷    //順序是從第1行的第1列一直到最后一列，然后第二行的第一列一直到最后 
    //一列，然后第三行的……    if (col == board.length) 
        return backTrace(board, row + 1, 0); 
    //如果當前位置已經有數字了，就不能再填了，直接到這一行的下一列    if (board[row][col] != '.') 
        return backTrace(board, row, col + 1); 
    //如果上面條件都不滿足，我們就從1到9中選擇一個合適的數字填入到數獨中 
    for (char i = '1'; i <= '9'; i++) { 
        //判斷當前位置[row，col]是否可以放數字i，如果不能放再判斷下        //一個能不能放，直到找到能放的為止，如果從1-9都不能放，就會下面 
        //直接return false 
        if (!isValid(board, row, col, i)) 
            continue;        //如果能放數字i，就把數字i放進去        board[row][col] = i;        //如果成功就直接返回，不需要再嘗試了        if (backTrace(board, row, col)) 
            return true; 
        //否則就撤銷重新選擇        board[row][col] = '.'; 
    }    //如果當前位置[row，col]不能放任何數字，直接返回false 
    return false; 
}//驗證當前位置[row，col]是否可以存放字符cprivate static boolean isValid(char[][] board, int row, int col, char c) { 
    for (int i = 0; i < 9; i++) { 
        if (board[i][col] != '.' && board[i][col] == c) 
            return false; 
        if (board[row][i] != '.' && board[row][i] == c) 
            return false; 
        if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] != '.' && 
                board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) 
            return false; 
    }    return true; 
} 

總結

回溯算法要和遞歸結合起來就很好理解了，遞歸分為兩部分，第一部分是先往下傳遞，第二部分到達終止條件的時候然后再反彈往回走，我們來看一下階乘的遞歸

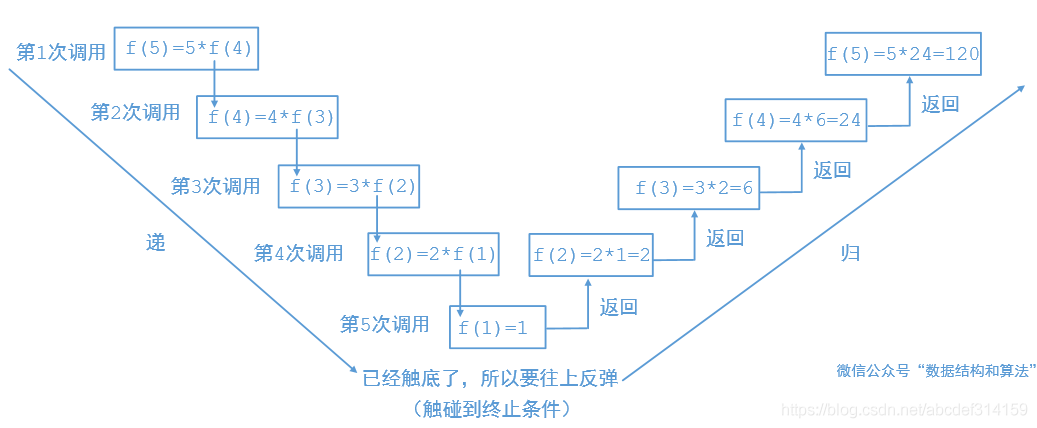
其實回溯算法就是在往下傳遞的時候把某個值給改變，然后往回反彈的時候再把原來的值復原即可。比如八皇后的時候我們先假設一個位置可以放皇后，如果走不通就把當前位置給撤銷，放其他的位置。如果是組合之類的問題，往下傳遞的時候我們把當前值加入到list中，然后往回反彈的時候在把它從list中給移除掉即可。