JDK 竟然是這樣實現棧的?
本文轉載自微信公眾號「Java中文社群」,作者磊哥 。轉載本文請聯系Java中文社群公眾號。
這正式開始之前,先給大家再解釋一下「堆棧」一詞的含義,因為之前有讀者對這個詞有一定的疑惑。
Stack 翻譯為中文是堆棧的意思,但為了能和 Heap(堆)區分開,因此我們一般將 Stack 簡稱為棧。因此當“堆棧”連在一起時有可能表示的是 Stack,而當“堆、棧”中間有分號時,則表示 Heap(堆)和 Stack(棧),如下圖所示:
JDK 棧的實現
聊會正題,接下來我們來看 JDK 中是如何實現棧的?
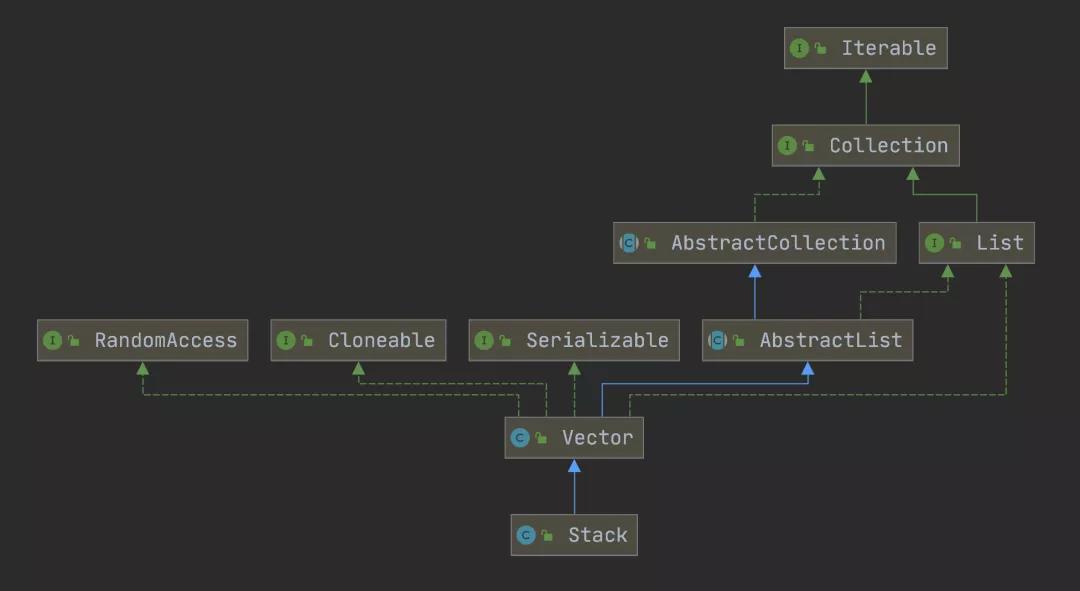
在 JDK 中,棧的實現類是 Stack,它的繼承關系如下圖所示:
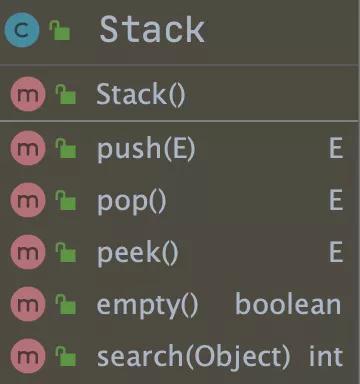
Stack 包含的方法如下圖所示:
其中最重要的方法有:
- push:入棧方法(添加數據);
- pop:出棧并返回當前元素(移除數據);
- peek:查詢棧頂元素。
Stack 實現源碼如下:
- public class Stack<E> extends Vector<E> {
- /**
- * 創建一個空棧
- */
- public Stack() {
- }
- /**
- * 入棧方法,調用的是 Vector#addElement 的添加方法
- */
- public E push(E item) {
- addElement(item);
- return item;
- }
- /**
- * 出棧并返回當前元素,調用的是 Vector#removeElementAt 的移除元素方法
- */
- public synchronized E pop() {
- E obj; // 返回當前要移除的棧頂元素信息
- int len = size();
- obj = peek(); // 查詢當前棧頂元素
- removeElementAt(len - 1); // 移除棧頂元素
- return obj;
- }
- /**
- * 查詢棧頂元素,調用 Vector#elementAt 的查詢方法
- */
- public synchronized E peek() {
- int len = size(); // 查詢當前棧的長度
- if (len == 0) // 如果為空棧,直接拋出異常
- throw new EmptyStackException();
- return elementAt(len - 1); // 查詢棧頂元素的信息
- }
- /**
- * 判斷棧是否為空
- */
- public boolean empty() {
- return size() == 0;
- }
- // 忽略其他方法...
- }
從上述源碼可以看出, Stack 中的核心方法中都調用了父類 Vector 類中的方法,Vector 類的核心源碼:
- public class Vector<E>
- extends AbstractList<E>
- implements List<E>, RandomAccess, Cloneable, java.io.Serializable
- {
- protected Object[] elementData; // 存儲數據的容器
- protected int elementCount; // 存儲數據的容量值
- /**
- * 添加數據
- */
- public synchronized void addElement(E obj) {
- modCount++; // 統計容器被更改的參數
- ensureCapacityHelper(elementCount + 1); // 確認容器大小,如果容量超出則進行擴容
- elementData[elementCount++] = obj; // 將數據存儲到數組
- }
- /**
- * 移除元素(根據下標移除)
- */
- public synchronized void removeElementAt(int index) {
- modCount++; // 統計容器被更改的參數
- // 數據正確性效驗
- if (index >= elementCount) {
- throw new ArrayIndexOutOfBoundsException(index + " >= " +
- elementCount);
- }
- else if (index < 0) {
- throw new ArrayIndexOutOfBoundsException(index);
- }
- int j = elementCount - index - 1;
- if (j > 0) { // 刪除的不是最后一個元素
- // 把刪除元素之后的所有元素往前移動
- System.arraycopy(elementData, index + 1, elementData, index, j);
- }
- elementCount--; // 數組容量 -1
- elementData[elementCount] = null; // 將末尾的元素賦值為 null(刪除尾部元素)
- }
- /**
- * 查詢元素(根據下標)
- */
- public synchronized E elementAt(int index) {
- // 安全性驗證
- if (index >= elementCount) {
- throw new ArrayIndexOutOfBoundsException(index + " >= " + elementCount);
- }
- // 根據下標返回數組中的元素
- return elementData(index);
- }
- // 忽略其他方法...
- }
對于上述源碼中,可以最不好理解的就是 System#arraycopy 這個方法,它的作用其實就是將刪除的元素(非末尾元素)的后續元素依次往前移動的,比如以下代碼:
- Object[] elementData = {"Java", "Hello", "world", "JDK", "JRE"};
- int index = 3;
- int j = elementData.length - index - 1;
- System.arraycopy(elementData, index + 1, elementData, index, j);
- // System.arraycopy(elementData, 4, elementData, 3, 1);
- System.out.println(Arrays.toString(elementData));
它的運行結果是:
- [Java, Hello, world, JRE, JRE]
也就是說當我們要刪除下標為 3 的元素時,需要把 3 以后的元素往前移動,所以數組的值就從 {"Java", "Hello", "world", "JDK", "JRE"} 變為了 [Java, Hello, world, JRE, JRE],最后我們只需要把尾部元素刪除掉,就可以實現數組中刪除非末尾元素的功能了。
小結
通過以上源碼可以得知,JDK 中的棧(Stack)也是通過物理結構數組實現的,我們通過操作物理數組來實現邏輯結構棧的功能。
棧的應用
經過前面的學習我們對棧已經有了一定的了解了,那棧在我們的平常工作中有哪些應用呢?接下里我們一起來看。
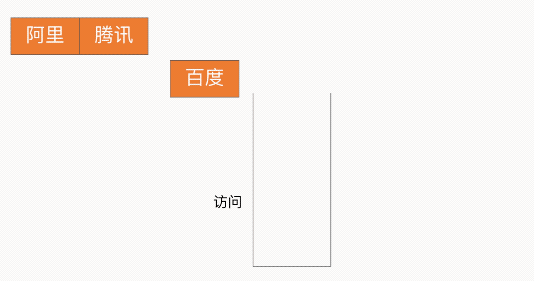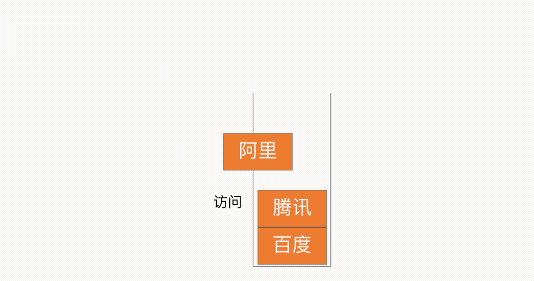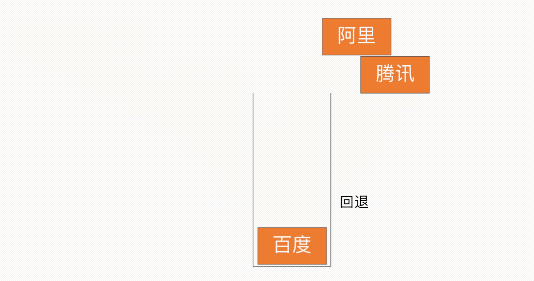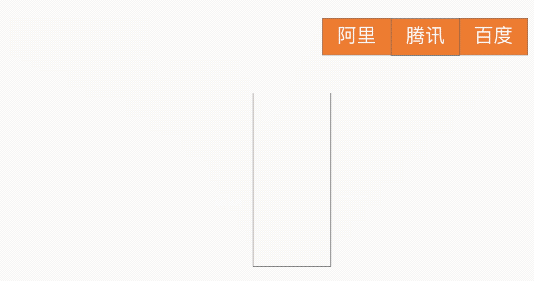
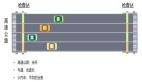
瀏覽器回退
棧的特性為 LIFO(Last In First Out,LIFO)后進先出,因此借助此特性就可以實現瀏覽器的回退功能,如下圖所示:
函數調用棧
棧在程序中最經典的一個應用就是函數調用棧了(或叫方法調用棧),比如操作系統給每個線程分配了一塊獨立的內存空間,這塊內存被組織成“棧”這種結構, 用來存儲函數調用時的臨時變量。每進入一個函數,就會將臨時變量作為一個棧幀入棧,當被調用函數執行完成,返回之后,將這個函數對應的棧幀出棧。為了讓你更好地理解,我們一塊來看下這段代碼的執行過程。
- int main() {
- int a = 1;
- int ret = 0;
- int res = 0;
- ret = add(3, 5);
- res = a + ret;
- System.out.println(res);
- reuturn 0;
- }
- int add(int x, int y) {
- int sum = 0;
- sum = x + y;
- return sum;
- }
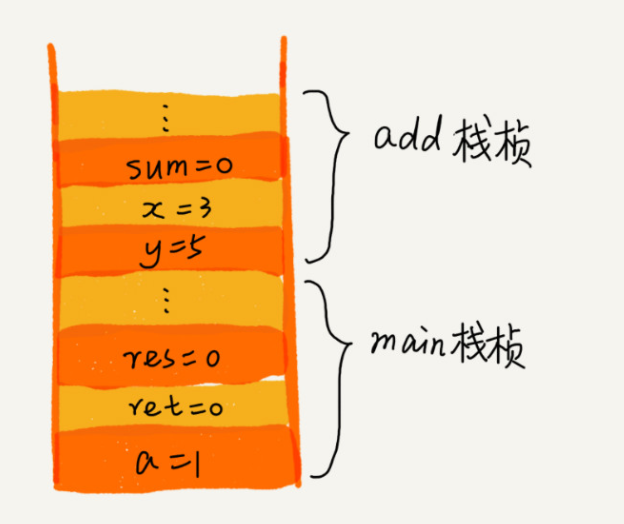
從代碼中我們可以看出, main() 函數調用了 add() 函數,獲取計算結果,并且與臨時變量 a 相加,最后打印 res 的值。為了讓你清晰地看到這個過程對應的函數棧里出棧、入棧的操作,我畫了一張圖。圖中顯示的是,在執行到 add() 函數時,函數調用棧的情況。
棧的復雜度
復雜度分為兩個維度:
- 時間維度:是指執行當前算法所消耗的時間,我們通常用「時間復雜度」來描述;
- 空間維度:是指執行當前算法需要占用多少內存空間,我們通常用「空間復雜度」來描述。
這兩種復雜度都是用大 O 表示法來表示的,比如以下代碼:
- int[] arr = {1, 2, 3, 4};
- for (int i = 0; i < arr.length; i++) {
- System.out.println(i);
- }
用大 O 表示法來表示的話,它的時間復雜度就是 O(n),而如下代碼的時間復雜度卻為 O(1):
- int[] arr = {1, 2, 3, 4};
- System.out.println(arr[0]); // 通過下標獲取元素
因此如果使用大 O 表示法來表示棧的復雜度的話,結果如下所示:
引用 & 鳴謝
https://time.geekbang.org/column/article/41222