高斯進程已經存在了一段時間，但它只是在過去5-10年，有一個大的復蘇，其興趣。部分原因是求解的計算復雜：由于他們的模型需要矩陣反轉，復雜性是 O(n3)，很難更快地獲得。正因為如此，它一直難以解決一段時間，因為計算能力一直如此薄弱，但在過去的幾年里，有這么多的研究和資金背后的ML，它變得更加可能。

高斯過程最酷的特征之一是它們非常非常相似的神經網絡。事實上，眾所周知，高斯進程(GP)相當于單層完全連接的神經網絡，其參數比其參數更具有 i.i.d. 。

我想說清楚這一點：下面的證據很簡單，但它具有深遠的影響。中央極限定理可以統一明顯復雜的現象，在這種情況下，性能最好的模型可以被視為機器學習模型的子集，該模型的領域尚未完全成熟。

是的，對GP的研究一直經受住考驗，但只是在過去幾年中，研究人員才開發出能夠對非線性模式(如跳躍)進行特征化的深高斯過程，而DNN的這種模式是做成的(特別是能夠對XOR邏輯進行建模)。因此，從這一點，我們可以看到，有這么多收獲。

我一直想研究一下這個證據， 下面很簡單。以下文章由李等人在谷歌腦的報紙上取，因此我要感謝他們讓本文如此方便。

有點符號

注意：您不能對"媒體"上的所有內容進行下標，因此，如果您看到下劃線(M_l)，則假設這意味著 M 與 l 作為下標。所以一個M_i + 米

考慮使用隱藏寬度層(對于層 L)N_l L 層完全連接的神經網絡。讓 x ∈ Rdɪ輸入到網絡，讓 z l 表示其輸出(在層 L)。l'th 層中激活的 i'th 組件表示為 xli 和 zli。l'th 層的權重和偏置參數具有 iid 的零值和偏置參數，并假定它們具有零均值和 σ 2_w/N_l。

神經網絡

現在我們知道神經網絡輸出 (zli) 的 i'th 組件的計算方式如下：

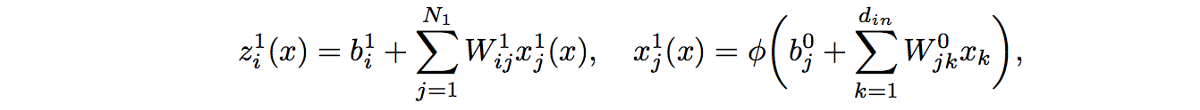
我們顯示了對輸入 x 的依賴性。由于權重和偏置參數假定為 iid，因此 xli 和 xli' 的 pos 激活函數對于 j=/j' 是獨立的。

現在，由于 zli(x) 是 iid 項的總和，它遵循中央限制定理，因此在無限寬度 (N1-> ∞) 的限制中，zli(x) 也因此高斯分布。

高斯進程

同樣，從多維CLT，我們可以推斷比任何有限集合的變量z將是聯合多變量高斯，這恰好是我們高斯過程的確切定義。

因此，我們可以得出結論，zli(x)=GP(μ 1，K1)是一個高斯過程，均值為μ 1，K1為協方差，它們本身與 i 無關。由于參數的均值為零，因此μ 1=0，但 K1(x，x') 如下所示：

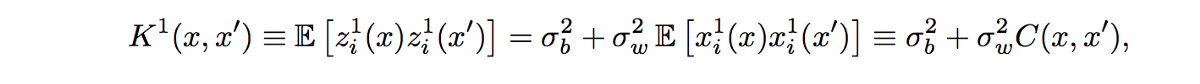
其中，通過針對W0和b0的分布進行整合獲得這種協方差。請注意，由于 i=/=j 的任何兩個 zli 和 zlj 都是共同的高斯，并且零協方差，因此盡管使用了隱藏層產生的相同功能，它們仍保證是獨立的。

一些證據是簡單和合乎邏輯的，中央極限定理的魔力是，它統一了高斯分布下的一切。高斯分布是偉大的，因為邊緣化和調節變量(或維度)導致高斯分布和功能形式是相當簡單的，所以事情可以濃縮成封閉形式的解決方案(所以很少需要優化技術)。

讓我知道你是怎么找到我的邏輯， 問問題， 如果你有任何問題， 請讓我知道， 如果我錯過了什么!

隨時了解我的最新文章!