資料來源：getwallpapers.com

深度學習是機器學習中重要分支之一。它的目的是教會計算機做那些對于人類來說相當自然的事情。深度學習也是無人駕駛汽車背后的一項關鍵性技術，可以幫無人車識別停車標志、區分行人與路燈柱。它是手機、平板、電視和免提揚聲器等設備實現語音控制的關鍵。深度學習近期以其前所未有的成果獲得了廣泛關注。

在深度學習中，計算機模型直接從圖像、文本或聲音中學習直接如何執行分類任務。深度學習模型可以達到最高的準確度，有時甚至超過了人類的水平。我們通常使用大量標記的數據和包含許多層的神經網絡體系結構來訓練模型。

資源

 

深度學習的模型可應用到各種復雜任務中：

1. 人工神經網絡（ANN）進行回歸和分類

2. 用于計算機視覺的卷積神經網絡（CNN）

3. 遞歸神經網絡（RNN）用于時間序列分析

4. 自組織地圖以進行特征提取

5. 推薦系統的深玻爾茲曼機

6. 推薦系統的自動編碼器

在本文中，我們將盡可能的介紹人工神經網絡（ANN）的所有相關內容。

“人工神經網絡（ANN）是一種信息處理范例，它受到生物神經系統（大腦）信息處理方式的啟發。由大量高度互連的處理元件（神經元）組成，這些元件協同工作以解決特定問題。”

主要內容：

1. 神經元

2. 激活功能

3. 激活功能的類型

4. 神經網絡如何工作

5. 神經網絡如何學習（反向傳播）

6. 梯度下降

7. 隨機梯度下降

8. 隨機梯度下降訓練神經網絡

神經元

神經元（也稱為神經細胞）是大腦和神經系統的基本單元，通過樹突接收來自外部世界的刺激信息，對該信息進行處理后，通過軸突輸出給其他細胞。

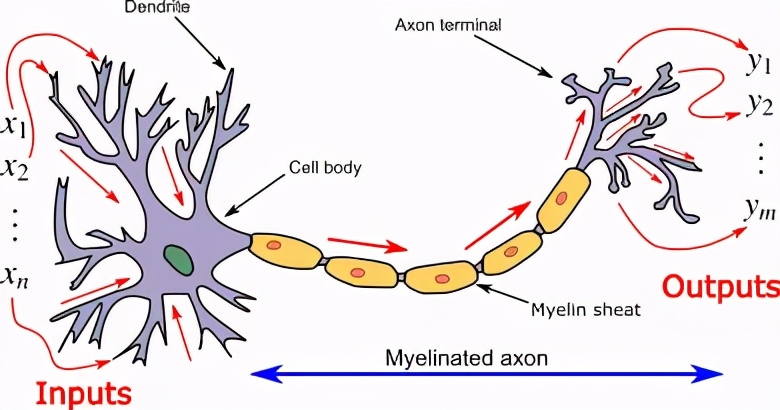
生物神經元

 

細胞體（Soma）：神經元細胞的主要部分，包含細胞核，進行必要的生化反應。

樹突：神經元周圍類似頭發的管狀結構。主要負責接受輸入信號。

軸突：這是一種細長的管狀結構，類似于傳輸線。

突觸：神經元以復雜的空間排列相互連接。軸突末端再次分支，是一種高度復雜、高度專一的結構，我們稱之為突觸。兩個神經元之間的聯系就發生在這些突觸處。

樹突接收其他神經元信息輸入。細胞體處理這些傳入信息，得到相應的輸出結果，該結果通過軸突和突觸發送到其他神經元。

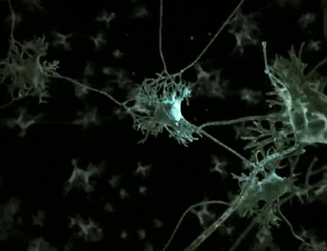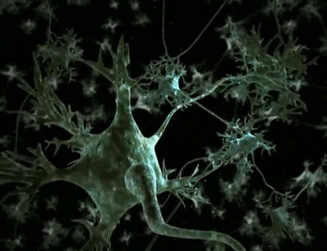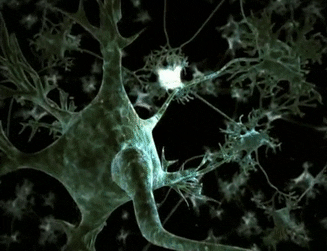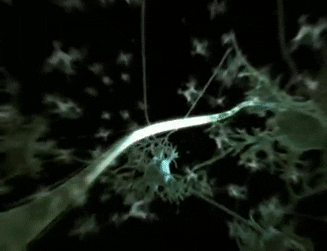
電信號流過神經元。

 

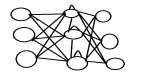
下圖代表了受生物神經元啟發的ANN一般模型。它也被稱為感知器。

單層神經網絡一般稱為感知器，給定輸入它將計算得到輸出。

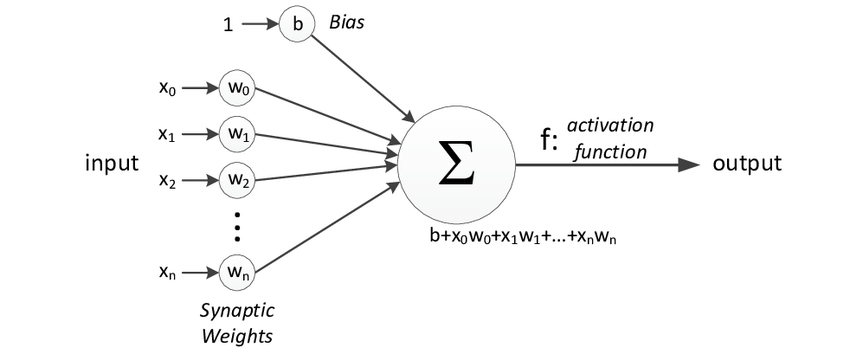
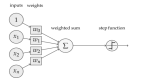
感知器

在上圖中，x0, x1, x2, x3...x(n)代表該網絡的輸入（獨立變量），每一個輸入在經過所謂的樹突時都要乘以相應的權重。該權重表示為w0, w1, w2, w3….w(n)，它顯示特定節點的強度。b是偏差值。偏差值可以向上或向下移動激活函數。

最簡單的情況，將這些乘積相加并輸入傳遞函數（激活函數）得到結果，然后將該結果作為輸出發送。

激活函數

激活函數對于ANN學習和理解真正復雜的東西很重要。它們的主要目的是將ANN中節點的輸入信號轉換為輸出信號，此輸出信號將作為下一層的輸入。

激活函數通過計算加權總和偏差值來決定是否激活該神經元。目的是引入非線性。

如果我們不應用激活函數，那么輸出信號將僅僅是線性函數（一階多項式）。線性函數很容易求解，功耗也相對較小，但是它們的復雜性受到一定的限制。因此沒有激活函數，我們的模型就無法進行學習，也無法對復雜的數據進行建模，例如圖像，視頻，音頻，語音等。

為什么我們需要非線性函數？

非線性函數是一種具有曲率的函數。現在我們需要神經網絡能夠進行學習，能夠表示將輸入映射到輸出的任意復雜函數。因此神經網絡也被認為是 “通用函數逼近器”。

激活函數的類型：

1. 閾值激活函數—（二進制階躍函數）

二進制階躍函數是基于閾值的激活函數。如果輸入值高于某個閾值，則神經元被激活并將完全相同的信號發送到下一層；低于某個閾值則不被激活。

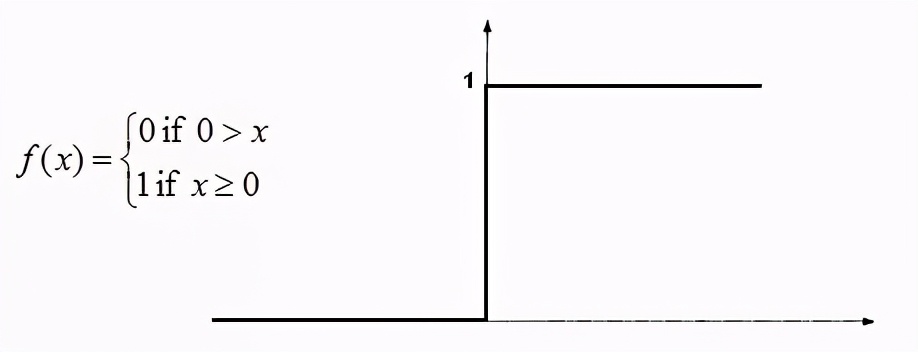
二進制函數

 

此函數的問題是創建一個二進制分類器（1或0），但是如果我們要連接多個這樣的神經元以引入更多類，如Class1、Class2、Class3等。在這種情況下，所有神經元都將給出1 ，我們將無法進行判斷。

2. Sigmoid激活函數-（邏輯函數）

Sigmoid函數是一種數學函數，具有特征性的“ S”形曲線或S型曲線，范圍在0到1之間，因此它用于需要預測概率為輸出。

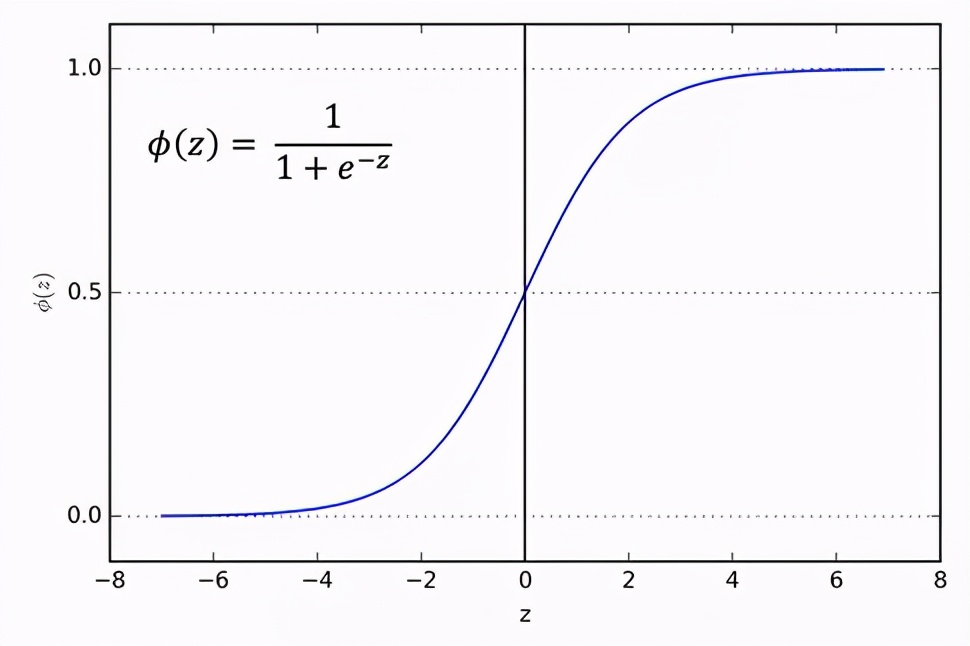
Sigmoid曲線

 

Sigmoid函數是可微的，這意味著我們可以求解任意2個點的曲線斜率。Sigmoid激活函數的缺點是，如果提供較大的負輸入，則可能導致神經網絡在訓練時卡住。

3. 雙曲正切函數—（tanh）

類似于Sigmoid，但性能更好。它本質上是非線性的，因此我們可以對各層進行疊加。該函數的范圍是（-1,1）。

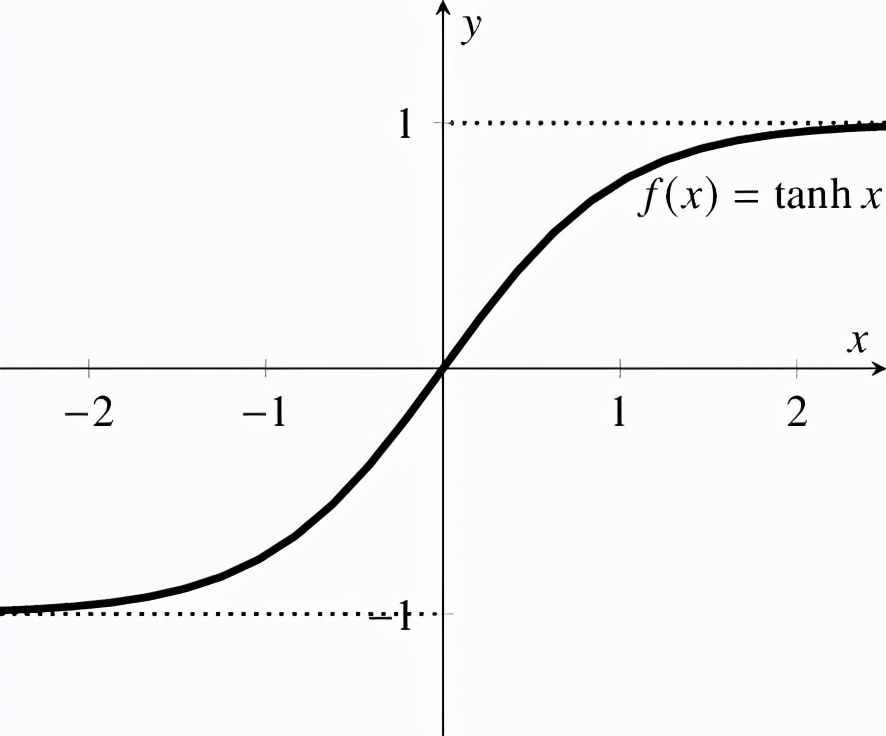
雙曲正切函數

此功能的主要優點是，負輸入映射為負輸出，而只有零值輸入會被映射為接近零輸出。因此，在訓練過程中卡頓的可能性較小。

4. 整流線性單元-（ReLu）

ReLu是CNN和ANN中最常用的激活函數，范圍從零到無窮大。[0，∞]

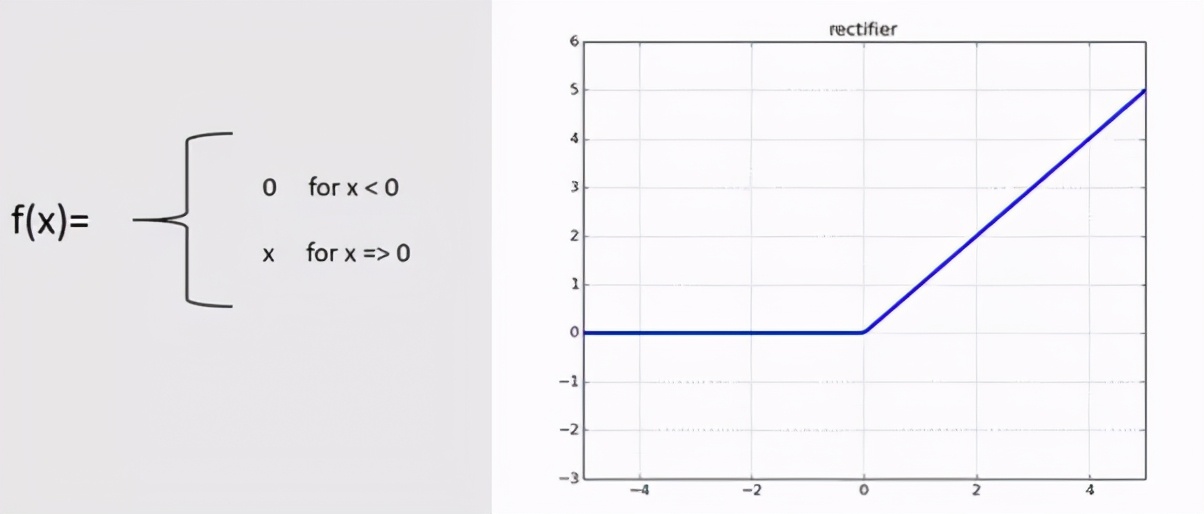
ReLu

如果x為正，則給出輸出為“ x”；如果x為負，否則輸出為0。ReLu看起來是線性函數的問題，但本質上是非線性的，并且ReLu的組合也是非線性的。實際上，它是一個很好的近似器，可以通過組合Relu來近似大部分函數。

它一般應用于神經網絡的隱藏層。對于輸出層而言，分類問題通常使用softmax函數，回歸問題使用線性函數。

這里存在的一個問題是，某些梯度在訓練過程中可能會消失。這會導致權重更新，任何數據點都無法激活該神經元。ReLu基本導致了神經元的死亡。

為了解決這一問題，引入了Leaky ReLu。Leaky ReLu引入了一個小斜率來保證不出現上述問題。Leaky ReLu范圍從-∞到+∞。

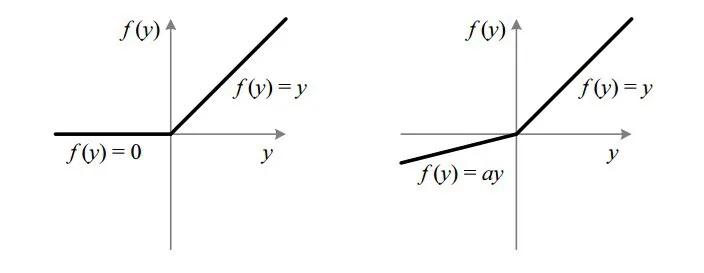
ReLu vs Leaky ReLu

 

Leaky增加了ReLu函數的輸出范圍。通常，a = 0.01。當a不為0.01時，則稱為隨機ReLu。

神經網絡如何工作？

讓我們以房地產價格為例，首先，我們將不同的因素匯總到一行數據中： Area, Bedrooms, Distance to city and Age.

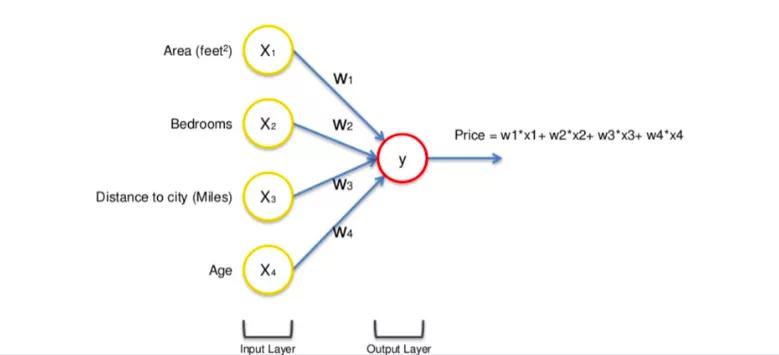
輸入值通過加權的突觸直接到達輸出層。四個輸入值均會被分析并輸入到激活函數中，產生輸出結果。

這很簡單，但是通過在輸入和輸出層之間添加一個隱藏層可以擴大神經網絡的功能并提高其準確性。

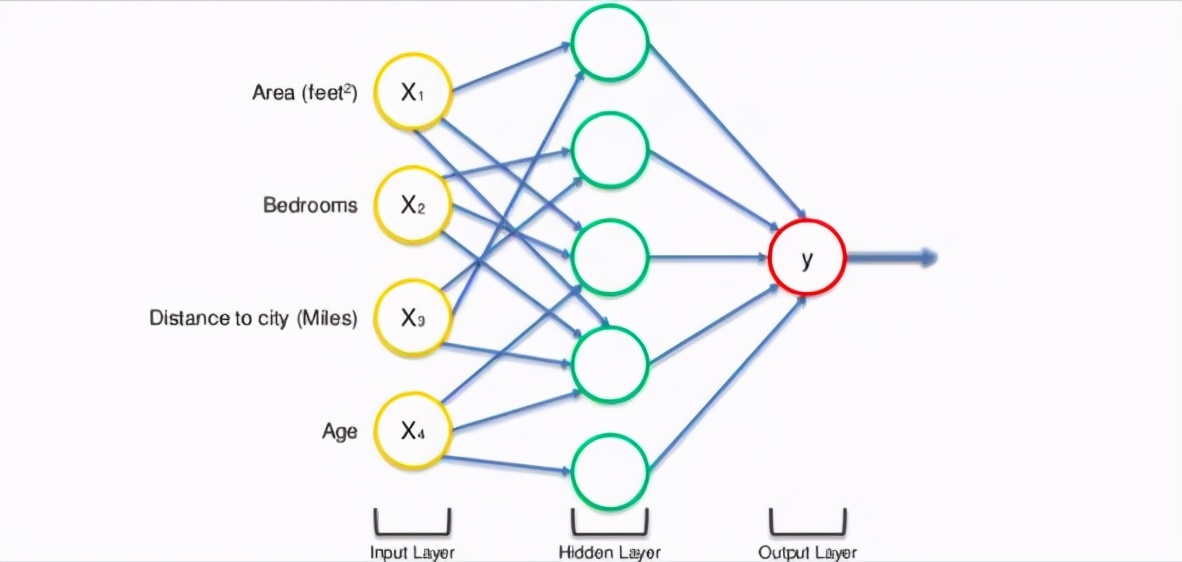
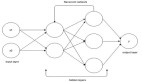
具有隱藏層的神經網絡（僅顯示非0值）

現在在上圖中，所有4個變量都通過突觸連接到神經元。但是，并非所有的突觸都被加權。權值包括0值和非0值。在這里，非零值表示重要性，0值表示輸入被丟棄。

讓我們以第一個神經元的Area和Distance to City為非零的示例為例，這意味著它們對第一個神經元重要。另外兩個變量，Bedrooms而Age權值為0，因此不通過第一神經元。

您可能想知道為什么第一個神經元只考慮四個變量中的兩個。距離城市越遠房子變得越便宜，這在房地產市場上很普遍。因此，這個神經元所做的事情可能是尋找離市區較近的房屋。

神經元很多，每個神經元用這些變量的不同組合進行相似的計算。一旦滿足標準，神經元就會使用激活函數進行計算。

下一個神經元加權的突觸可能是Distance to the city和Bedrooms。因此神經元以非常靈活的方式工作，全面的搜索以查找特定的事物。

神經網絡如何學習？

讓我們先來做一個類比。神經網絡的學習與我們正常的學習方式密切相關，我們首先完成一定的工作，并得到教練的糾正，下一次以更好的方式來完成這個工作。類似地，神經網絡需要培訓者，來描述該網絡對輸入做出的反應。用實際值和預測值之間的差異，計算一個誤差值（也稱為成本函數），并將其發送回系統。

成本函數：實際值與輸出值之間平方差的一半。

對于網絡的每一層，都會分析成本函數，并用其調整下一個輸入的閾值和權重。我們的目標是使成本函數最小化。成本函數越低，實際值就越接近于預測值。這樣隨著網絡的不斷學習，每次運行的誤差都減小。

我們通過整個神經網絡反饋結果數據。將輸入變量連接到神經元的加權突觸是我們唯一可以控制的事情，因此只要實際值和預測值之間存在差異，我們就需要調整權重。一旦稍微調整它們并再次運行神經網絡，便會產生一個新的成本函數，我們希望它可以比上一個小。重復此過程，直到將成本函數降低到盡可能小的水平為止。

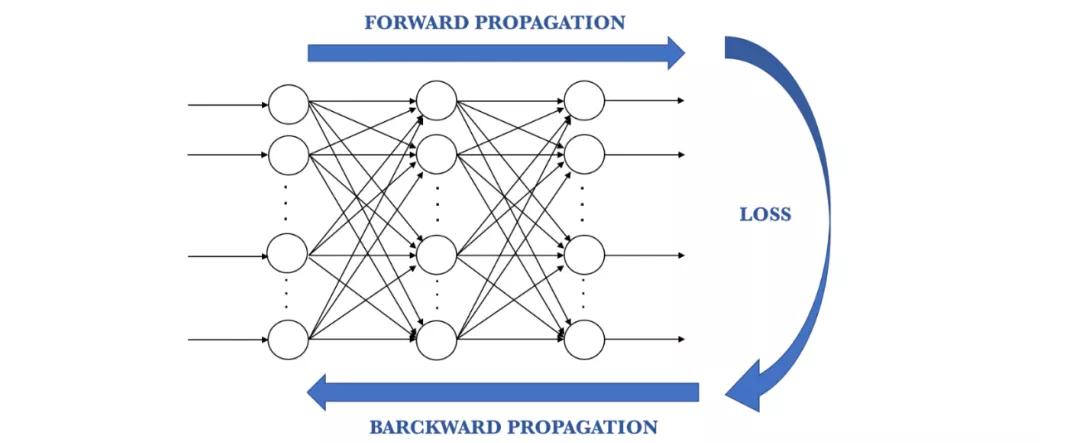
上述過程稱為反向傳播，并通過網絡連續進行，直到將誤差值保持在最小值為止。

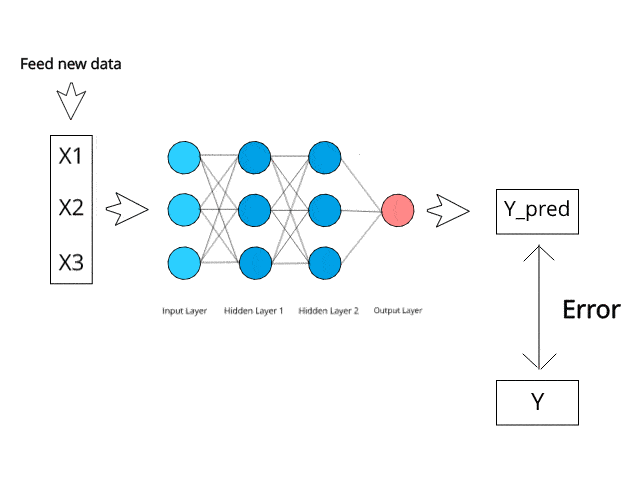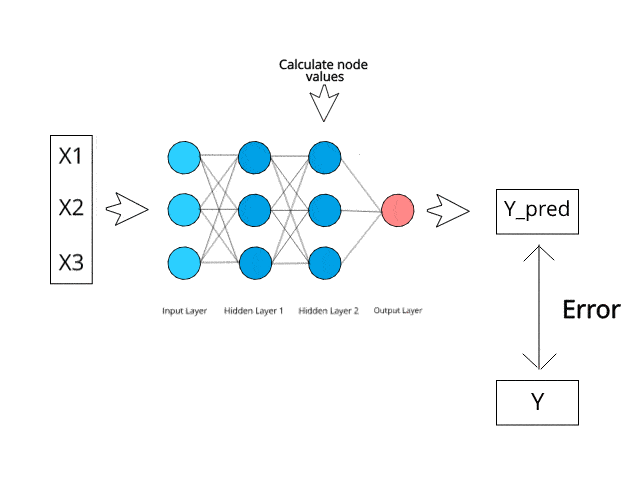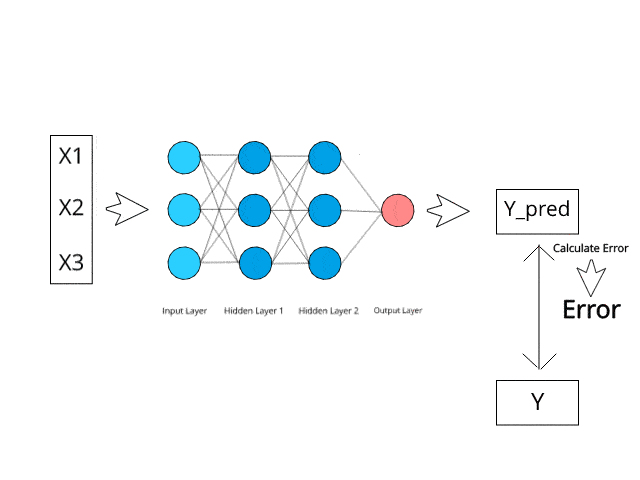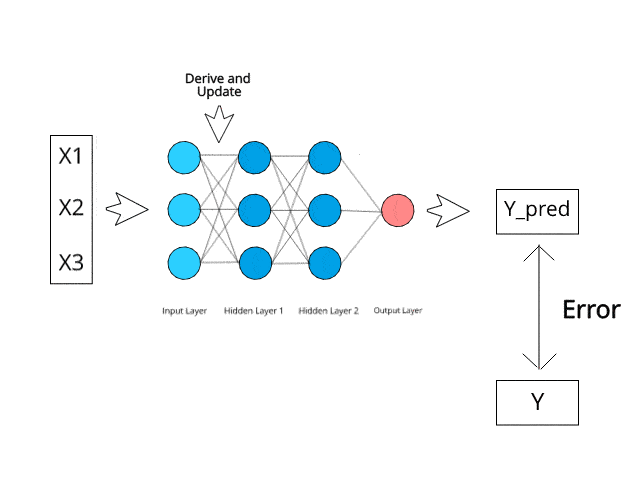
反向傳播

調整權重的方法有兩種：
1.蠻力方法
2.批梯度下降

蠻力法

適合單層前饋網絡。在這里，我們需要考慮許多可能的權重。在這種方法中，我們想要舍棄除U形曲線底部權值以外的所有其他權重。最佳權值可以使用簡單的消除技術找到。如果我們只需要優化一個權重，那么這種方法很有效。但如果是具有許多權重的復雜神經網絡，該方法將因維數太高而無法實現。

分批梯度下降

它是一階迭代優化算法，在訓練具有不同權重模型的過程中找到最小成本值（損失）。

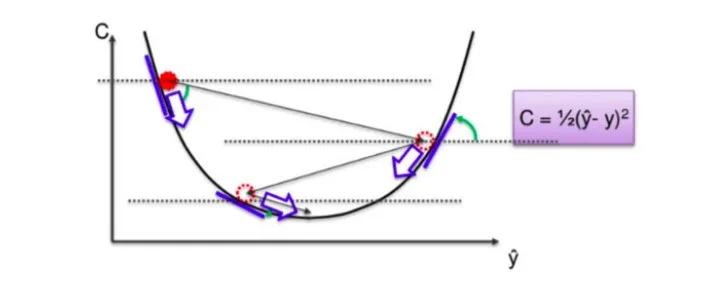
梯度下降

在“梯度下降”過程中，我們不會一次都查看每個權重并剔除錯誤的權重，而是查看函數斜率。

如果斜率→負值，則表示您沿著曲線下降。
如果斜率→正，則不執行任何操作

這樣，可以消除大量不正確的權重。

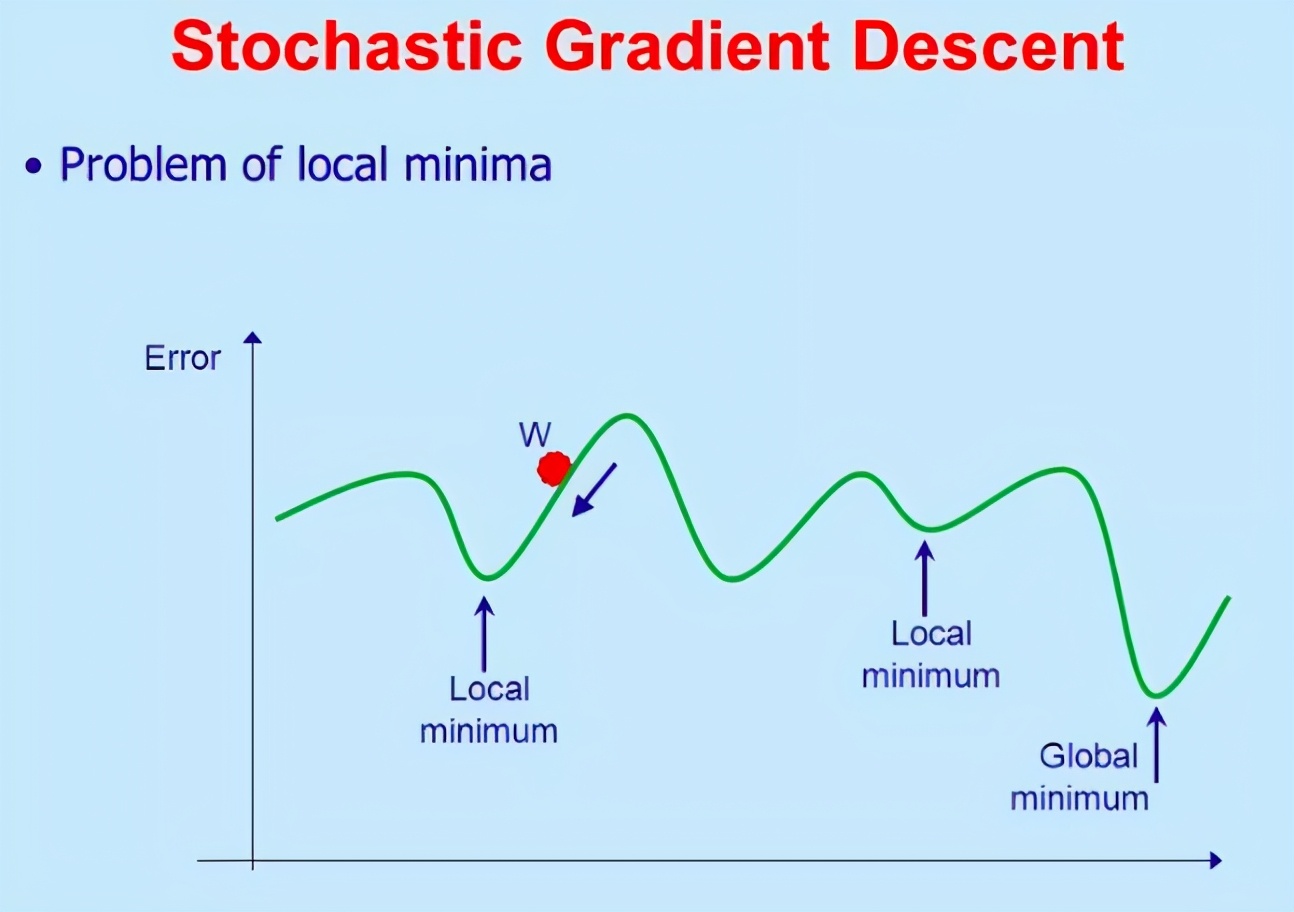
隨機梯度下降（SGD）

如上圖所示，當我們具有凸曲線時，漸變下降效果很好。但是，如果我們沒有凸曲線，則漸變下降將失敗。

“ 隨機 ” 一詞是指與隨機概率相關的系統或過程。因此，在隨機梯度下降中，隨機選擇一些樣本，而不是每次迭代的整個數據集。

隨機梯度下降

在SGD中，我們一次獲取一行數據，通過神經網絡運行該數據，然后調整權重。對于第二行，我們運行它，然后比較Cost函數，然后再次調整權重。

SGD幫助我們避免了局部極小值的問題。它比Gradient Descent快得多，因為它一次運行每一行，并且不必將整個數據加載到內存中即可進行計算。

要注意的一件事是，由于SGD通常比典型的Gradient Descent噪聲更大，因此由于其下降的隨機性，通常需要更多的迭代次數才能達到最小值。盡管與典型的Gradient Descent相比，它需要更多的迭代次數才能達到最小值，但在計算消耗上仍比典型的Gradient Descent少得多。因此，在大多數情況下，SGD優于分批梯度下降。

利用隨機梯度下降訓練神經網絡

步驟1→將權重隨機初始化為接近0但不為0的小數。

步驟2→在輸入層中輸入數據集的第一個觀測值，每個要素放在一個節點中。

步驟3→ 正向傳播：從左到右，神經元按順序被激活，直到獲得預測值。每個神經元的影響都受權重的限制。

步驟4→將預測結果與實際結果進行比較，并測量的誤差（成本函數）。

步驟5→ 反向傳播：從右到左，誤差反向傳播。根據它們對錯誤造成的影響來更新權重。學習率決定了我們更新權重的程度。

步驟6→重復步驟1至5，并在每次比較后更新權重（強化學習）

步驟7→當整個訓練集通過ANN時，就完成了。

結論

資料來源：techcrunch.com

神經網絡是一個全新的新概念，它還有很大潛力。可以應用于各種不同的概念中，并在測試階段通過特定的反向傳播和糾錯機制進行學習。這些多層系統也許可以有一天僅靠學習來減少發生錯誤的可能性，而無需人工糾正。