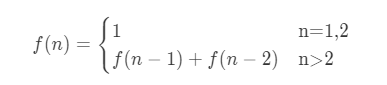如何掌握動態規劃算法的套路?
動態規劃(Dynamic Programming),簡稱DP,這個名字給人的感覺是一種非常高大上非常復雜的算法,很多同學看到這個名字可能就會望而卻步,在面試的時候也非常害怕被問到動態規劃的題目。實際上,它并不是不是一種確定的算法,它是一種最優化的方法求解問題的思想或方法。它是由美國數學家貝爾曼(Bellman)在研究多階段決策過程的優化問題時提出。不過,與之對應的還有一些與時間無關的靜態規劃,如:線性規劃、非線性規劃等。在運籌學中,動態規劃是的非常重要的內容,在各個行業領域都有著廣泛的應用。我們如何理解動態規劃?
如果一個問題的最優解可以通過其子問題的最優解經過推導得到,那么,我們就可以先求出其子問題的最優解,根據子問題的解得出原問題的最優解。如果子問題有較多的重復出現,為了減少重復計算,降低時間復雜度,則可以自底向上從最終子問題向原問題逐步求解并先將子問題存儲起來,在求解大的子問題時可以直接從表中查詢子問題的解,這就是動態規劃的基本思想。
簡單來來理解就是將一個大問題簡化成若干子問題,并存入一個表中,再根據數據表中子問題的解求出大問題的解。這種算法看上去是不是很熟悉?其實,動態規劃和分治算法類似,我們也常常將其和分治算法進行比較。它們都需要將其分解成若干子問題并求解子問題。不同的是分治算法是自頂向下求解各子問題,然后合并子問題的解從而得到原問題的解;而動態規劃是將子問題拆解之后,自底向上求解子問題的解并將存儲結果存儲起來,在求解大的子問題時直接查詢子問題的解,算法效率也將大大的提高。
理論描述太過生硬和枯燥,我們直接來看一個例子。
斐波那契數列
斐波那契數列
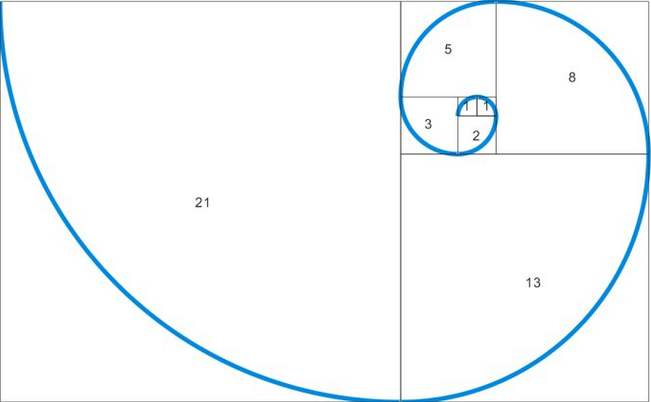
斐波那契數列是一個非常神奇的數列,它由意大利數學家萊昂納-斐波那契提出,其特征是數列某一項的值是前兩項的和,也可以稱作黃金分割數列。
萊昂納多·斐波那契
我們可以用下面的通項公式來表示斐波那契數列。
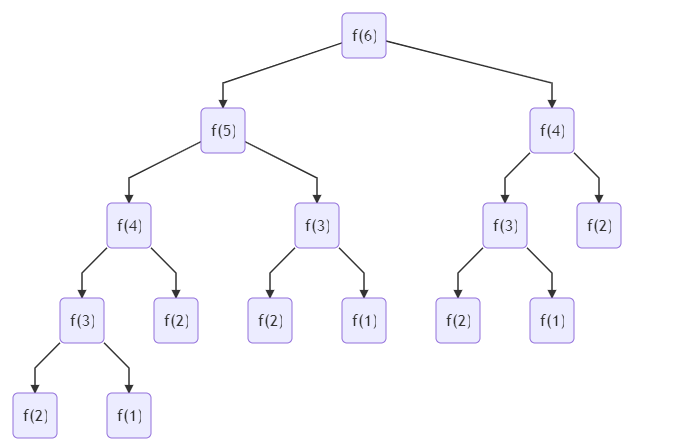
從斐波那契數列的公式中可知,數列的第n(n>2)項的值f(n)等于f(n)+f(n-1),如果要求得f(n)值就需要先求得f(n-1)和f(n-2)的值,為了便于分析,我們當假設n=6,我們可以按照下圖進行分解,一步步分解成小的值。
斐波那契
看了上面的圖,想必大家腦海中一種想到了程序的實現,我們可以直接通過遞歸的方法就可以求出n項的值,程序很容易,如下所示。
- int fib(int n)
- {
- if(n==1 || n==2) return 1;
- return fib(n-1) + fib(n-2);
- }
但是,很明顯這種算法是指數時間復雜度O(2^n),其復雜度會隨著n的增加成指數增長,當n取到一定大時,將需要很長的時間,顯然這不是一種最優的算法。不過,仔細觀察上圖的各個分解項,我們會發現圖中有很多重復的子項,這就是上面這種遞歸算法復雜度較高的原因。那么,還能不能進行優化呢?答案是肯定的。
我們可以通過動態規劃的思想來優化上面這個算法,為了避免大量的重復計算,我們可以從最底層的子問題開始計算,并通過一個表來存儲這些子問題的值,當再次遇到這個值就不需要再重新計算。
如下面的程序,我們從最小的子問題n=1,2開始向上計算,并且定義了一個vector容器用來存儲被計算過的子問題的值,下次再計算大問題時直接調用容器里的值即可。
- int fib(int n)
- {
- vector<int> dp(n, 0);
- dp[0] = dp[1] = 1;
- for (int i = 2; i < n; i++)
- {
- dp[i] = dp[i - 1] + dp[i - 2];
- }
- return dp[n-1];
- }
很明顯上面的這種算法,大大降低了算法的時間復雜度,現在的時間復雜度就是O(n)了。不過,雖然時間復雜度降低了,這卻是犧牲了空間換取過來的。實際上我們還可以進一步去優化,從公式上我們分析可以看出,要求出某一項的值我們需要先求出其前兩項子問題的值,當我們自下而上求解子問題的過程中,我們直接保存連續兩項子問題的值即可。
- int fib(int n)
- {
- int dp[2]={1,1};
- for (int i = 2; i < n; i++)
- {
- int tmp = dp[0];
- dp[0] = dp[1];
- dp[1] = dp[1] + tmp;
- }
- return dp[1];
- }
最長上升子序列
嚴格意義上來說,上面的斐波那契數列也不完全算是動態規劃問題。因為從動態規劃的定義上來看,動態規劃問題一般滿足三個性質:
- 最優化原理:如果原問題的最優解所分解出的子問題的解也是最優的,我們就稱該問題具有最優子結構,原問題的最優解可以由子問題的最優解推導得出;
- 無后效性:某階段狀態一旦確定,這個狀態以后決策的影響,它只與當前狀態有關;
- 有重疊子問題:子問題可能會在下一階段決策中被重復多次用到。
根據動態規劃問題的這三個性質我們再看另外一個例子,最長上升子序列(Longest Increasing Subsequence)問題,簡稱LIS,這是一個非常經典的動態規劃問題。
有一個長度為n的數列a0, a1, ..., a(n-1),求出這個序列中最長的上升子序列的長度。所謂上升子序列指的是對于任意的i
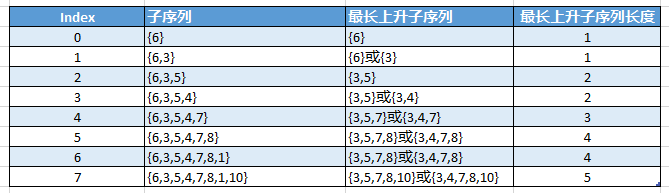
我們先將原問題進行分解,依次拆解成子問題,如下表:
子序列
我們的代碼可以按照下面來實現,其中,程序里我們用dp數組保存各個子序列以nums[i]結尾的最長子序列長度,max存儲最長子序列的長度。
- int maxLIS(std::vector<int>& nums)
- {
- int max = 1;
- std::vector<int> dp(nums.size(), 1);
- for(int i = 1;i< nums.size(); i++)
- {
- for(int j=0; j<i; j++)
- {
- if(nums[i]>nums[j])
- {
- dp[i] = dp[j] + 1;
- }
- max = std::max(dp[i], max);
- }
- }
- return max;
- }
通過上面的兩個例子,大家都學廢了嗎?常見的還有很多問題可以使用動態規劃的方法解決,比如,背包問題,硬幣找零,最短路徑等。動態規劃不是一種固定的算法,對應的問題也是多種多樣,但大家只要掌握了其基本的思想,就可以輕松的解出相應的問題,大家趕快去嘗試一下吧!
本文轉載自微信公眾號「Will的大食堂」,可以通過以下二維碼關注。轉載本文請聯系Will的大食堂公眾號。