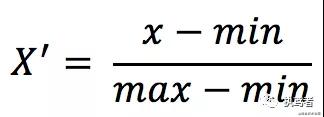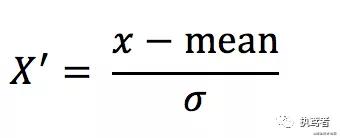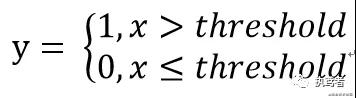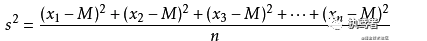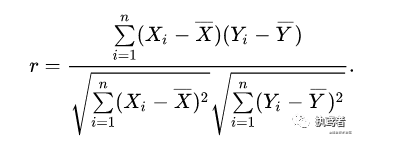[[374893]]

背景:

近年來機器學習的熱度不斷升高，前端領域也在不斷布局，從大的研究方向來看，有前端智能化、端智能；從框架這個角度來看，也有很多js版的框架，例如TensorFlow.js、Ml.js、Brain.js等。雖然當前來看其在前端落地的應用還不是很多，但是把握趨勢就是把握未來。本文將通過上下兩篇來對機器學習的內容進行闡述，這是第一篇，主要介紹一些基礎知識和特征工程；后續(xù)推出的一批主要利用闡述機器學習中的監(jiān)督學習算法和非監(jiān)督學習算法。

一、基礎

1.1 定義

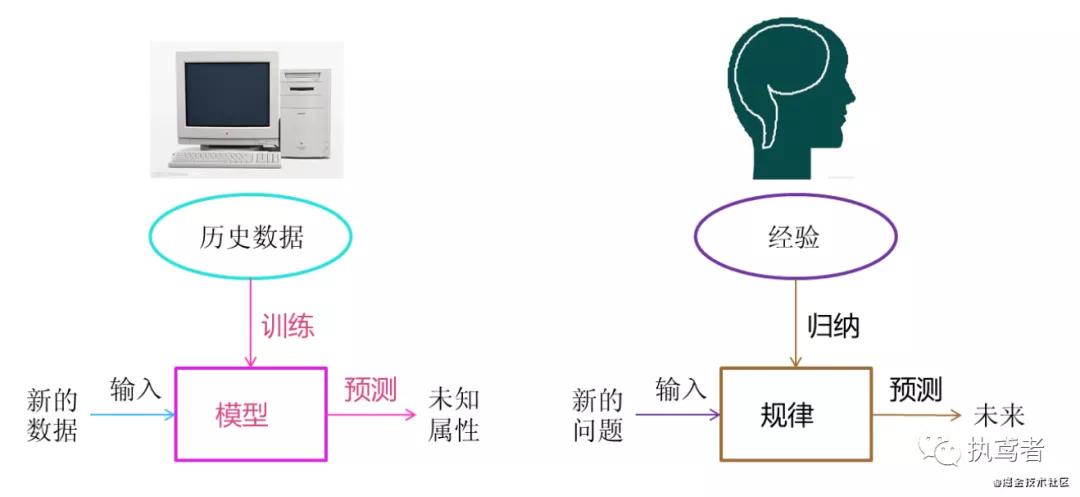
機器學習是從數(shù)據(jù)中自動分析獲得模型，并利用模型對未知數(shù)據(jù)進行預測。

 

1.2 算法分類

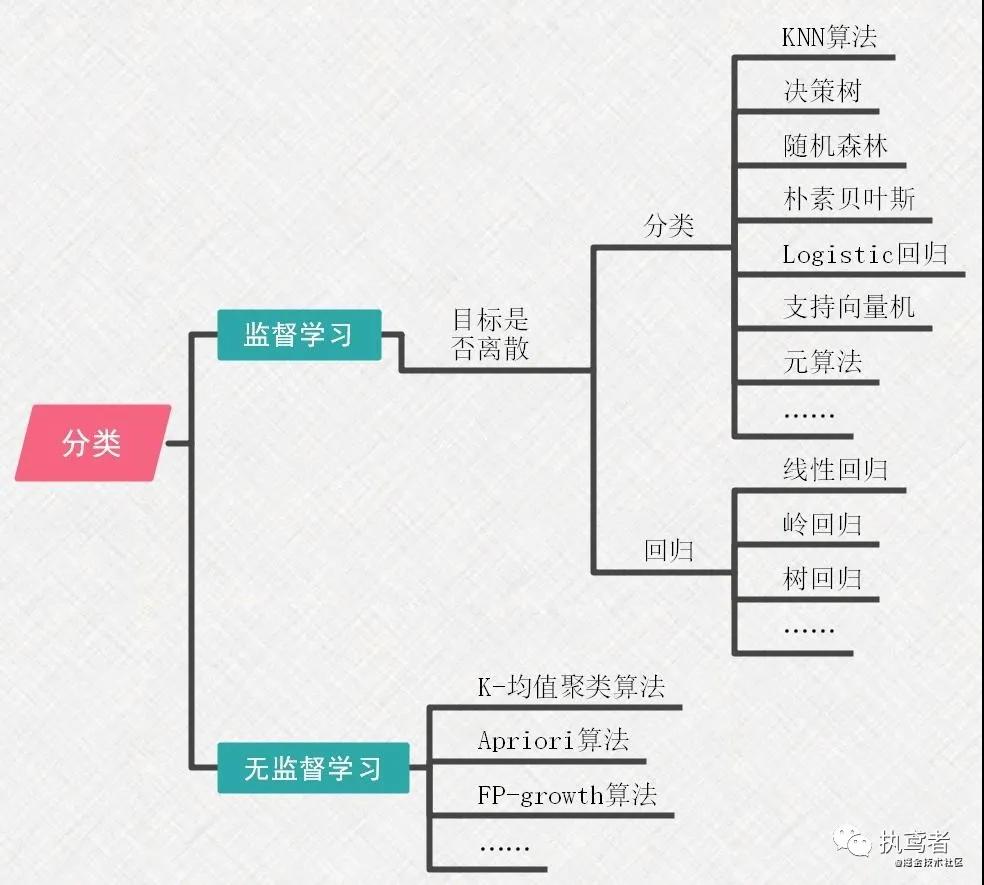
機器學習的前提是數(shù)據(jù)，根據(jù)數(shù)據(jù)中是否有目標可以劃分為：監(jiān)督學習算法和無監(jiān)督學習算法。

• 監(jiān)督學習算法——輸入數(shù)據(jù)是由輸入特征值和目標值所組成。
• 無監(jiān)督學習算法——輸入數(shù)據(jù)是由輸入特征值和目標值所組成

 

1.3 如何選擇合適算法

機器學習有這么多算法，面對一個問題時應該如何選擇合適的算法成為了不可避免的問題，下面就來敘述兩條選擇合適算法的黃金法則。

1.確定使用機器學習算法的目的。

• 將數(shù)據(jù)劃分為離散的組是唯一需求——聚類算法
• 除將數(shù)據(jù)劃分為離散的組，還需要估計數(shù)據(jù)與每個組的相似度——密度估計算法
• 目標變量為離散型——分類算法
• 目標變量為連續(xù)型——回歸算法
• 若想要預測目標變量的值——監(jiān)督學習算法
• 若無目標變量值——無監(jiān)督學習

2.需要分析或收集的數(shù)據(jù)是什么，了解其數(shù)據(jù)特征

• 特征值是離散型變量還是連續(xù)型變量
• 特征值中是否存在缺失的值
• 何種原因造成缺失值
• 數(shù)據(jù)中是否存在異常值
• 某個特征發(fā)生的頻率如何
• ……

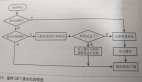
1.4 整體流程

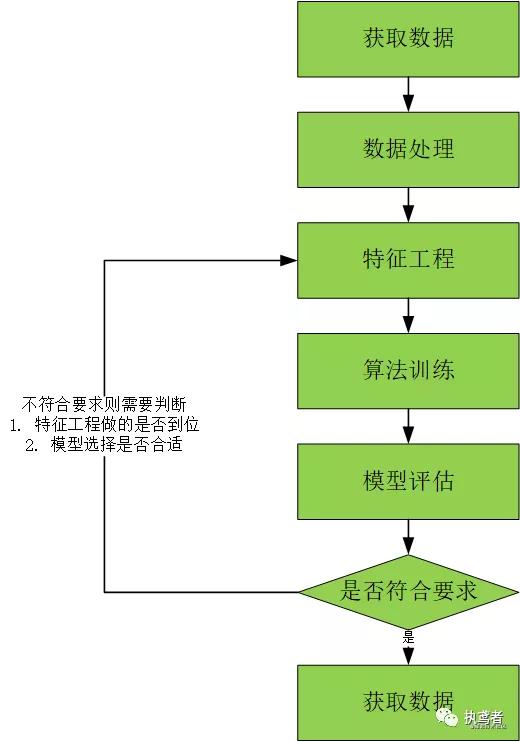
不管多么復雜的內容經過前人的總結最會有一套方法論供我們這樣的小白使用，下面就來闡述一下機器學習通用的流程。

 

獲取數(shù)據(jù)

獲取數(shù)據(jù)是機器學習的第一步，例如使用公開的數(shù)據(jù)源、爬蟲獲取數(shù)據(jù)源、日志中獲取數(shù)據(jù)、商業(yè)數(shù)據(jù)等。

數(shù)據(jù)處理

得到數(shù)據(jù)后并不一定符合使用需求，所以需要進行數(shù)據(jù)清洗、數(shù)據(jù)填充、數(shù)據(jù)格式轉換，達到減小訓練的數(shù)據(jù)量，加快算法的訓練時間的目的。

特征工程

特征工程是使用專業(yè)背景知識和技巧處理數(shù)據(jù)，使得特征能在機器學習算法上發(fā)揮更好的作用的過程,直接影響機器學習的效果，主要包含特征提取、特征預處理、特征降維。

算法訓練

將處理之后的數(shù)據(jù)輸入到合適的算法進行訓練。

模型評估

使用測試集來評估模型的性能.模型性能指標有很多，比如在分類模型中常用的有錯誤率，精準率，召回率，F(xiàn)1指標，ROC等。

應用

將機器學習算法轉換為應用程序執(zhí)行實際任務，從而檢驗該算法是否可以在實際工作中正常使用。

二、特征工程

業(yè)界流傳著一句話 “數(shù)據(jù)決定了機器學習的上限，而算法只是盡可能逼近這個上限”，這里的數(shù)據(jù)指的就是經過特征工程處理后的數(shù)據(jù)。特征工程是使用專業(yè)背景知識和技巧處理數(shù)據(jù)，使得特征能在機器學習算法上發(fā)揮更好的作用的過程，可見特征工程在機器學習中的重要地位。對于特征工程主要分為三步：特征抽取、特征預處理、特征降維。

注：特征工程是一個很深的學科，此處不展開闡述。

2.1 特征提取

特征提取指的就是將任意數(shù)據(jù)(如文本或圖像)轉換為可用于機器學習的數(shù)字特征，常用的主要包含：字典特征提取、文本特征提取、圖像特征提取。

2.2 特征預處理

通過特征提取，能得到未經處理的特征,該特征具有以下問題：

量綱不同：特征可能具有量綱，導致其特征的規(guī)格不一樣，容易影響(支配)目標結果，使得一些算法無法學習到其它的特征，需要進行無量綱化處理。

信息冗余：對于某些定量特征，其包含的有效信息為區(qū)間劃分，需要進行二值化處理。

定性特征不能直接使用：某些機器學習算法和模型只接受定量特征的輸入，則需要將定性特征轉換為定量特征，可通過啞編碼實現(xiàn)。

2.2.1 無量綱化

無量綱化使不同規(guī)格的數(shù)據(jù)轉換到同一規(guī)則，常用方法有歸一化和標準化

1.歸一化

• 定義

對原始數(shù)據(jù)進行線性變換，使得結果映射到[0,1]之間。

• 計算公式

 

• 特點

最大最小值容易受到異常點影響，穩(wěn)定性較差。

2.標準化

• 定義

將原始數(shù)據(jù)進行變換到均值為0、標準差為1的范圍內

• 計算公式

 

• 特點

較少的異常點對結果影響不大，穩(wěn)定性較好。

2.2.2 定量特征二值化

對于定量特征可進行二值化，通過選取一個合適的閾值，大于某閾值的為1，小余等于某閾值的為0。

 

2.2.3 定性特征啞編碼

大部分算法對于定性特征無法訓練模型，利用啞編碼(one-hot)可以將定性特征處理為定量特征用于模型訓練，其基本思想是：將離散特征的每一種值看成一種狀態(tài)，若該特征有N個值，則存在N種狀態(tài)，例如女孩子的頭發(fā)按照辮子的多少可以劃分為：無辮子、一個辮子、兩個辮子、多個辮子，則該特征有4種狀態(tài)，利用啞編碼可以表示為：

• 無辮子 ====》[1, 0, 0, 0]
• 一個辮子 ====》[0, 1, 0, 0]
• 兩個辮子 ====》[0, 0, 1, 0]
• 多個辮子 ====》[0, 0, 0, 1]

2.3 特征降維

在機器學習中對維度較高的數(shù)據(jù)進行處理時會極大消耗系統(tǒng)資源，甚至產生維度災難。在某些限定條件下，通過降維的方式可降低隨機變量的個數(shù)，用一個低維度向量來表示原始高維度的特征。常用的降維的方式有：特征選擇、PCA、LDA等。

2.3.1 特征選擇

數(shù)據(jù)預處理完畢之后需要選擇有意義的特征進行訓練，特征選擇從以下兩方面考慮：

特征是否發(fā)散：若某特征不發(fā)散(例如方差接近為0)，則認為該特征無差異。

特征與目標的相關性：優(yōu)先選擇與目標相關性較高的特征。

常用的特征選擇方式有：Filter(過濾法)、Wrapper(包裝法)、Embedded(集成法)。

2.3.1.1 Filter(過濾法)

先進行特征選擇，然后去訓練學習器，其特征選擇的過程與學習器無關。其主要思想是給每一維的特征賦予權重，權重代表該特征的重要性，然后設定閾值或者待選擇閾值的個數(shù)選擇特征。常用方法有方差選擇法(低方差特征過濾)、相關系數(shù)法等。

一、低方差特征過濾

方差指的是各變量值與其均值離差平方的平均數(shù)，是測算數(shù)值型數(shù)據(jù)離散程度的重要方法，方差越大則表征數(shù)據(jù)的離散程度越大，反之越小。對于數(shù)據(jù)中的特征值，方差小則表示特征大多樣本的值比較相近;方差大則表示特征很多樣本的值都有差別。低方差特征過濾正是基于該思想，通過設定方差閾值來去掉小于該閾值的特征。方差計算公式如下：

 

二、相關系數(shù)法

皮爾遜相關系數(shù)(r)定義為兩個變量之間的協(xié)方差和標準差的商，是反映變量之間相關關系密切程度的統(tǒng)計指標，其值r范圍為[-1, 1]，含義為：

• 當r > 0時表示兩變量正相關
• r < 0時，兩變量為負相關
• 當|r|=1時，表示兩變量為完全相關
• 當r=0時，表示兩變量間無相關關系
• 當0<|r|<1時，表示兩變量存在一定程度的相關。且|r|越接近1，兩變量間線性關系越密切;|r|越接近于0，表示兩變量的線性相關越弱

 

2.3.1.2 Wrapper(包裝法)

把要使用的分類器作為特征選擇的評價函數(shù)，對于特定的分類器選擇最優(yōu)的特征子集。其主要思想是將子集的選擇看作是一個搜索尋優(yōu)問題，生成不同的組合，對組合進行評價，再與其它的組合進行比較。常用方法有遞歸特征消除法。

• 遞歸特征消除的主要思想是反復的構建模型(如SVM或者回歸模型)然后選出最好的(或者最差的)的特征(可以根據(jù)系數(shù)來選)，把選出來的特征選擇出來，然后在剩余的特征上重復這個過程，直到所有特征都遍歷了。這個過程中特征被消除的次序就是特征的排序。因此，這是一種尋找最優(yōu)特征子集的貪心算法。

2.3.1.3 Embedded(集成法)

將特征選擇嵌入到模型訓練當中。其主要思想是通過使用某些機器學習的算法和模型進行訓練，得到各個特征的權值系數(shù)，根據(jù)系數(shù)從大到小選擇特征。常用方法有：基于懲罰項的特征選擇法(L1、L2)、決策樹的特征選擇法(信息熵、信息增益)。

注：該方法與算法強相關，所以在算法實現(xiàn)的時候進行闡述。

2.3.2 PCA(主成分分析法)

主成分分析(Principal components analysis，PCA)是一種分析、簡化數(shù)據(jù)集的技術。主成分分析經常用于減少數(shù)據(jù)集的維數(shù)，同時保持數(shù)據(jù)集中的對方差貢獻最大的特征(旨在找到數(shù)據(jù)中的主成分，并利用這些主成分表征原始數(shù)據(jù)，從而達到降維的目的)。這是通過保留低階主成分，忽略高階主成分做到的。

一、 優(yōu)缺點

1.優(yōu)點：

• 降低數(shù)據(jù)的復雜性，識別最重要的多個特征
• 僅需方差衡量信息量，不受數(shù)據(jù)集以外的因素影響
• 各主成分之間正交，可消除原始數(shù)據(jù)成分間的相互影響的因素
• 計算方法簡單，主要運算式特征值分解，易于實現(xiàn)

2.缺點：

可能損失有用信息(由于沒有考慮數(shù)據(jù)標簽，容易將不同類別數(shù)據(jù)完全混合在一起，很難區(qū)分)

• 二適用數(shù)據(jù)類型——數(shù)值型數(shù)據(jù)

2.3.3 LDA(線性判別分析法)

LDA是一種監(jiān)督學習的降維技術，它的數(shù)據(jù)集的每個樣本是有類別輸出的。PCA與此不同，PCA是不考慮樣本類別輸出的無監(jiān)督降維技術。LDA的思想是“最大化類間距離和最小化類內距離”(將數(shù)據(jù)在低維度上進行投影，投影后希望每一種類別數(shù)據(jù)的投影點盡可能的接近，而不同類別的數(shù)據(jù)的類別中心之間的距離盡可能的大)

1.優(yōu)點：

• 在降維過程中可以使用類別的先驗知識經驗
• LDA在樣本分類信息依賴均值而不是方差的時候，比PCA之類的算法較優(yōu)

2.缺點：

• LDA不適合對非高斯分布(非正態(tài)分布)樣本進行降維
• LDA降維后可降為[1, 2，……，k-1]維，其中k為類別數(shù)
• LDA在樣本分類信息依賴方差而不是均值的時候，降維效果不好
• LDA可能過度擬合數(shù)據(jù)

參考文獻

 

• 特征工程到底是什么
• LDA和PCA降維
• 機器學習實戰(zhàn)

本文轉載自微信公眾號「執(zhí)鳶者」，可以通過以下二維碼關注。轉載本文請聯(lián)系執(zhí)鳶者公眾號。