網絡安全攻防:密碼技術之公鑰密碼
對稱密碼可以實現對任意明文的高效加密,通常用于通信會話的加密,但隨著對稱加密應用越來越廣,會話密鑰的管理問題也隨之面臨挑戰。假設網絡中有n個實體需要兩兩通信,那么每個實體必須維護一把與其他任意一個實體之間的會話密鑰,總的會話密鑰數量為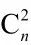 ,即達到O(n2)的量級,密鑰管理的復雜度明顯增加。另一方面,分組加密主要依賴于多輪復合的擴散和混淆運算,安全強度有待進一步增強。
,即達到O(n2)的量級,密鑰管理的復雜度明顯增加。另一方面,分組加密主要依賴于多輪復合的擴散和混淆運算,安全強度有待進一步增強。
公鑰密碼也稱非對稱密碼,即加密密鑰和解密密鑰不同,一個可被公開的密鑰被稱為公鑰,一個私人專用保管的密鑰被稱為私鑰。公鑰與私鑰在數學上是有緊密關系的,用公鑰加密的信息只能用對應的私鑰解密,反之亦然。由于公鑰算法不需要聯機密鑰服務器,密鑰分配變得簡單。一個人可以在與許多人交往時使用相同的密鑰對,而不必與每個人分別使用不同的密鑰。只要私鑰是保密的,就可以隨意分發其公鑰,用戶可以與任意數目的人員共享一個密鑰對,而不必為每個人單獨設立一個密鑰,顯著降低了密鑰管理復雜度,簡化了密鑰管理操作,有效提高了密碼學的可用性。
公鑰加密是一種干擾信息的方法,使用該方法的雙方擁有一對密鑰,其中一個可以公開分享,而另一個只有預定的目標接收方才知曉。任何人都可能使用私人的公開密鑰對信息進行加密。但是,只要預定接收方的解密密鑰被安全地保護起來,信息就無法被解密。一般而言,公鑰算法的設計依賴于經典的數論難題,即將攻擊者在沒有私鑰的情況下,破解一個公鑰加密系統,等效映射到求解數論難題。這樣,攻擊者若能在沒有私鑰的情況下破解公鑰加密,等效于其求解了公知的數論難題。這樣的模型假設也因此成為公鑰密碼安全的保障基石。
1976年,Whitfield Diffie和Martin Hellman 共同發表了學術論文《New Direction in Cryptography》,創建了公鑰加密體制。公鑰加密是重大的創新,從根本上改變了加密和解密的過程,也成為40年來信息安全應用領域的一項核心技術。2015年,Diffie和Hellman兩位密碼學家也因創立發明公鑰加密技術而獲得有著計算機領域諾貝爾美譽的圖靈獎。
1. Diffie-Hellman密鑰交換算法
下面以Alice和Bob為例介紹以Diffie和Hellman命名的DH密鑰交換原理。
(1)選定一個可公開的大質數p和底數g。
(2)Alice和Bob分別選定一個私有的素數a和b。
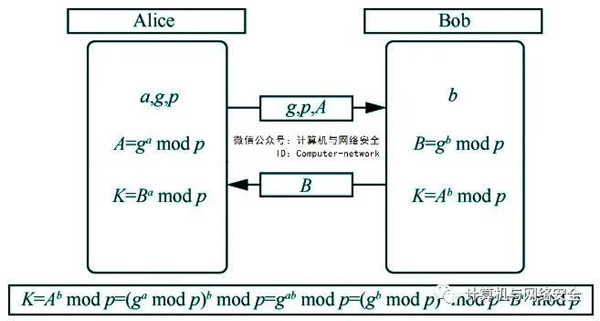
圖1給出了Alice和Bob通過公開交換g、p、A、B,最終各自計算獲得共享密鑰K=gab的基本過程。DH密鑰協商的目的是讓Alice和Bob安全獲得共享密鑰,任何第三方實體即使截獲雙方通信數據,也無法計算得到相同的密鑰。
圖1 DH密鑰交換原理
下面再看一個簡單的實例,來說明Alice和Bob協商計算會話密鑰K的過程。
1)Alice與Bob協定使用p=23,g=5。
2)Alice選擇一個秘密整數a=6,計算A=gamodp并發送給Bob:A=56mod 23=8。
3)Bob選擇一個秘密整數b=15,計算B=gbmodp并發送給Alice:B=515mod 23=19。
4)Alice計算K=Bamodp,即196mod 23=2。
5)Bob計算K=Abmodp,即815mod 23=2。
DH是一個公鑰算法,應用的數論難題是大數的離散對數求解難題,即已知g、a,計算A=ga是容易的,但反之,已知A和g,求解a是困難的。這樣,攻擊者即便截獲得到A和B,也無法計算得到a和b,因而也無法計算獲得K。
2. RSA公鑰算法
公開密鑰算法是在 1976年由當時在美國斯坦福大學的 Diffie和Hellman 兩人首先發明的,但是目前最流行的RSA算法則是1977年由MIT教授Ronald L.Rivest、Adi Shamir和Leonard M.Adleman共同發明的。RSA也是分別取自3名數學家人名的第一個字母。RSA算法依賴于大數因子分解難題,即給定兩個大素數p、q,計算它們的乘積n=pq是容易的,但反之,給定n,求解p和q是一個經典的數論難題。
(1)密鑰生成
①選擇兩個大素數:p和q。
②計算歐拉函數:φ(n)=(p−1)(q−1)。
③選擇一個正整數e,使gcd(e,φ(n))=1,即e和φ(n)互為素數。
④根據de=1(modφ(n)),利用Euclid算法計算出d。
⑤公鑰即為K=<e,n>。
⑥私鑰即為S=<d,p,q>。
(2)公鑰加密
①記明文信息為m(二進制),將m分成等長數據塊m1,m2,…,mi,塊長s,其中2s≤n。
②加密:ci≡mi^e(modn)
③解密:mi≡ci^d(modn)
一開始,RSA選用的n長度達到512 bit時,以當時的計算機運算能力,安全性已公認足夠強大。隨著并行計算水平的飛速發展以及量子計算等新型計算的出現,RSA的安全強度也開始受到威脅。目前,RSA選用的公鑰長度已達到了4 096 bit。
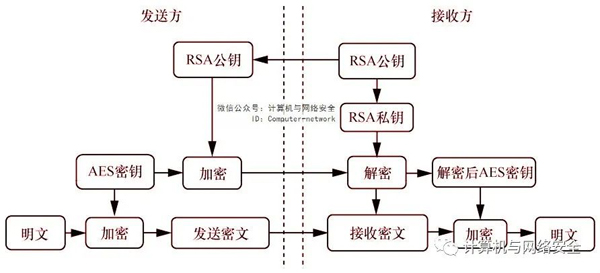
相比于對稱密碼,公鑰密碼具有實現難度大、安全強度大、計算耗費大等特點。因此,在日常應用時,RSA算法和AES算法混合使用,通常被稱作數字信封技術,如圖2所示。
圖2 數字信封技術
雖然安全強度大,但由于 RSA 公鑰加密需耗費較大資源,因此通常會話加密采用的是AES分組密碼,而AES會話密鑰則可通過RSA公鑰加密,AES密鑰的加密結果隨會話密文一起發送給接收方,這樣的技術就叫數字信封,可以確保僅有持有RSA私鑰的合法的接收方才能解開AES密鑰,從而獲得最終的會話明文。