[[384337]]

本文轉載自微信公眾號「小郎碼知答」，作者Simon郎。轉載本文請聯系小郎碼知答公眾號。    

背景

在我們這個日益追求高效的世界，我們對任何事情的等待都顯得十分的浮躁，網頁頁面刷新不出來，好煩，電腦打開運行程序慢，又是好煩!那怎么辦，技術的產生不就是我們所服務么，今天我們就聊一聊緩存這個技術，并使用我們熟知的數據結構--用鏈表實現LRU緩存淘汰算法。

在學習如何使用鏈表實現LRU緩存淘汰算法前，我們先提出幾個問題，大家好好思考下，問題如下：

• 什么是緩存，緩存的作用?
• 緩存的淘汰策略有哪些?
• 如何使用鏈表實現LRU緩存淘汰算法，有什么特點，如何優化?

好了，我們帶著上面的問題來學進行下面的學習。

1、什么是緩存，緩存的作用是什么?

緩存可以簡單的理解為保存數據的一個副本，以便于后續能夠快速的進行訪問。以計算機的使用場景為例，當cpu要訪問內存中的一條數據時，它會先在緩存里查找，如果能夠找到則直接使用，如果沒找到，則需要去內存里查找;

同樣的，在數據庫的訪問場景中，當項目系統需要查詢數據庫中的某條數據時，可以先讓請求查詢緩存，如果命中，就直接返回緩存的結果，如果沒有命中，就查詢數據庫， 并將查詢結果放入緩存，下次請求時查詢緩存命中，直接返回結果，就不用再次查詢數據庫。

通過以上兩個例子，我們發現無論在哪種場景下，都存在這樣一個順序：先緩存，后內存;先緩存，后數據庫。但是緩存的存在也占用了一部分內存空間，所以緩存是典型的以空間換時間，犧牲數據的實時性，卻滿足計算機運行的高效性。

仔細想一下，我們日常開發中遇到緩存的例子還挺多的。

• 操作系統的緩存

減少與磁盤的交互

• 數據庫緩存

減少對數據庫的查詢

• Web服務器緩存

減少對應用服務器的請求

• 客戶瀏覽器的緩存

減少對網站的訪問

2、緩存有哪些淘汰策略?

緩存的本質是以空間換時間，那么緩存的容量大小肯定是有限的，當緩存被占滿時，緩存中的那些數據應該被清理出去，那些數據應該被保留呢?這就需要緩存的淘汰策略來決定。

事實上，常用的緩存的淘汰策略有三種：先進先出算法(First in First out FIFO);淘汰一定時期內被訪問次數最少的頁面(Least Frequently Used LFU);淘汰最長時間未被使用的頁面(Least Recently Used LRU)

這些算法在不同層次的緩存上執行時具有不同的效率，需要結合具體的場景來選擇。

2.1 FIFO算法

FIFO算法即先進先出算法，常采用隊列實現。在緩存中，它的設計原則是：如果一個數據最先進入緩存中，則應該最早淘汰掉。

FIFO算法

新訪問的數據插入FIFO隊列的尾部，隊列中數據由隊到隊頭按順序順序移動

隊列滿時，刪除隊頭的數據

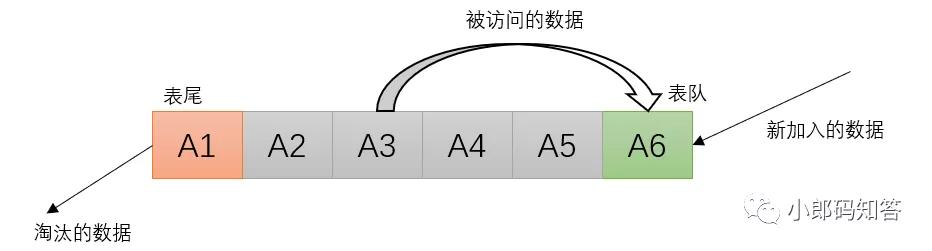
2.2 LRU算法

LRU算法是根據對數據的歷史訪問次數來進行淘汰數據的，通常使用鏈表來實現。在緩存中，它的設計原則是：如果數據最近被訪問過，那么將來它被訪問的幾率也很高。

LRU算法

• 新加入的數據插入到鏈表的頭部
• 每當緩存命中時(即緩存數據被訪問)，則將數據移到鏈表頭部
• 當來鏈表已滿的時候，將鏈表尾部的數據丟棄

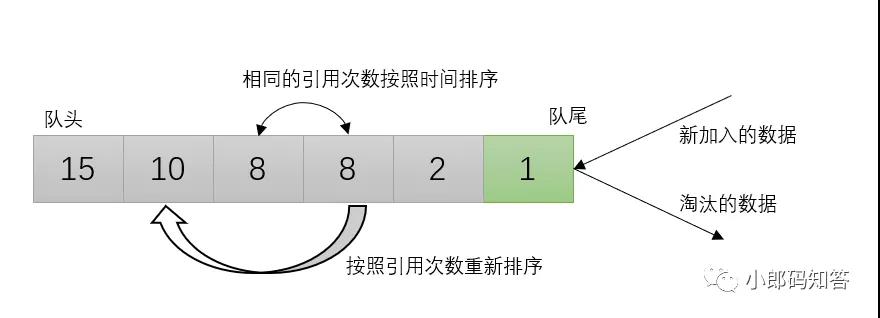
2.3 LFU算法

LFU算法是根據數據的歷史訪問頻率來淘汰數據，因此，LFU算法中的每個數據塊都有一個引用計數，所有數據塊按照引用計數排序，具有相同引用計數的數據塊則按照時間排序。在緩存中，它的設計原則是：如果數據被訪問多次，那么將來它的訪問頻率也會更高。

LFU算法

• 新加入數據插入到隊列尾部(引用計數為1;
• 隊列中的數據被訪問后，引用計數增加，隊列重新排序;
• 當需要淘汰數據時，將已經排序的列表最后的數據塊刪除。

3、如何使用鏈表實現緩存淘汰，有什么特點，如何優化?

在上面的文章中我們理解了緩存的概念及淘汰策略，其中LRU算法是筆試/面試中考察比較頻繁的，我秋招的時候，很多公司都讓我手寫了這個算法，為了避免大家采坑，下面，我們就手寫一個LRU緩存淘汰算法。

我們都知道鏈表的形式不止一種，我們應該選擇哪一種呢?

思考三分鐘........

好了，公布答案!

事實上，鏈表按照不同的連接結構可以劃分為單鏈表、循環鏈表和雙向鏈表。

• 單鏈表
  • 每個節點只包含一個指針，即后繼指針。
  • 單鏈表有兩個特殊的節點，即首節點和尾節點，用首節點地址表示整條鏈表，尾節點的后繼指針指向空地址null。
  • 性能特點：插入和刪除節點的時間復雜度為O(1)，查找的時間復雜度為O(n)。
• 循環鏈表
  • 除了尾節點的后繼指針指向首節點的地址外均與單鏈表一致。
  • 適用于存儲有循環特點的數據，比如約瑟夫問題。
• 雙向鏈表
  • 節點除了存儲數據外，還有兩個指針分別指向前一個節點地址(前驅指針prev)和下一個節點地址(后繼指針next)
  • 首節點的前驅指針prev和尾節點的后繼指針均指向空地址。

雙向鏈表相較于單鏈表的一大優勢在于：找到前驅節點的時間復雜度為O(1)，而單鏈表只能從頭節點慢慢往下找，所以仍然是O(n).而且，對于插入和刪除也是有優化的。

我們可能會有問題：單鏈表的插入刪除不是O(1)嗎?

是的，但是一般情況下，我們想要進行插入刪除操作，很多時候還是得先進行查找，再插入或者刪除，可見其實是先O(n),再O(1)。

因為我們需要刪除操作，刪除一個節點不僅要得到該節點本身的指針，也需要操作其它前驅節點的指針，而雙向鏈表能夠直接找到前驅，保證了操作時間復雜度為O(1)，因此使用雙向鏈表作為實現LRU緩存淘汰算法的結構會更高效。

算法思路

維護一個雙向鏈表，保存所有緩存的值，并且最老的值放在鏈表最后面。

當訪問的值在鏈表中時：將找到鏈表中值將其刪除，并重新在鏈表頭添加該值(保證鏈表中 數值的順序是從新到舊)

當訪問的值不在鏈表中時：當鏈表已滿：刪除鏈表最后一個值，將要添加的值放在鏈表頭 當鏈表未滿：直接在鏈表頭添加

3.1 LRU緩存淘汰算法

極客時間王爭的《數據結構與算法之美》給出了一個使用有序單鏈表實現LRU緩存淘汰算法，代碼如下：

public class LRUBaseLinkedList<T> { 
 
    /** 
     * 默認鏈表容量 
     */ 
    private final static Integer DEFAULT_CAPACITY = 10; 
 
    /** 
     * 頭結點 
     */ 
    private SNode<T> headNode; 
 
    /** 
     * 鏈表長度 
     */ 
    private Integer length; 
 
    /** 
     * 鏈表容量 
     */ 
    private Integer capacity; 
 
    public LRUBaseLinkedList() { 
        this.headNode = new SNode<>(); 
        this.capacity = DEFAULT_CAPACITY; 
        this.length = 0; 
    } 
 
    public LRUBaseLinkedList(Integer capacity) { 
        this.headNode = new SNode<>(); 
        this.capacity = capacity; 
        this.length = 0; 
    } 
 
    public void add(T data) { 
        SNode preNode = findPreNode(data); 
 
        // 鏈表中存在，刪除原數據，再插入到鏈表的頭部 
        if (preNode != null) { 
            deleteElemOptim(preNode); 
            intsertElemAtBegin(data); 
        } else { 
            if (length >= this.capacity) { 
                //刪除尾結點 
                deleteElemAtEnd(); 
            } 
            intsertElemAtBegin(data); 
        } 
    } 
 
    /** 
     * 刪除preNode結點下一個元素 
     * 
     * @param preNode 
     */ 
    private void deleteElemOptim(SNode preNode) { 
        SNode temp = preNode.getNext(); 
        preNode.setNext(temp.getNext()); 
        temp = null; 
        length--; 
    } 
 
    /** 
     * 鏈表頭部插入節點 
     * 
     * @param data 
     */ 
    private void intsertElemAtBegin(T data) { 
        SNode next = headNode.getNext(); 
        headNode.setNext(new SNode(data, next)); 
        length++; 
    } 
 
    /** 
     * 獲取查找到元素的前一個結點 
     * 
     * @param data 
     * @return 
     */ 
    private SNode findPreNode(T data) { 
        SNode node = headNode; 
        while (node.getNext() != null) { 
            if (data.equals(node.getNext().getElement())) { 
                return node; 
            } 
            node = node.getNext(); 
        } 
        return null; 
    } 
 
    /** 
     * 刪除尾結點 
     */ 
    private void deleteElemAtEnd() { 
        SNode ptr = headNode; 
        // 空鏈表直接返回 
        if (ptr.getNext() == null) { 
            return; 
        } 
 
        // 倒數第二個結點 
        while (ptr.getNext().getNext() != null) { 
            ptr = ptr.getNext(); 
        } 
 
        SNode tmp = ptr.getNext(); 
        ptr.setNext(null); 
        tmp = null; 
        length--; 
    } 
 
    private void printAll() { 
        SNode node = headNode.getNext(); 
        while (node != null) { 
            System.out.print(node.getElement() + ","); 
            node = node.getNext(); 
        } 
        System.out.println(); 
    } 
 
    public class SNode<T> { 
 
        private T element; 
 
        private SNode next; 
 
        public SNode(T element) { 
            this.element = element; 
        } 
 
        public SNode(T element, SNode next) { 
            this.element = element; 
            this.next = next; 
        } 
 
        public SNode() { 
            this.next = null; 
        } 
 
        public T getElement() { 
            return element; 
        } 
 
        public void setElement(T element) { 
            this.element = element; 
        } 
 
        public SNode getNext() { 
            return next; 
        } 
 
        public void setNext(SNode next) { 
            this.next = next; 
        } 
    } 
 
    public static void main(String[] args) { 
        LRUBaseLinkedList list = new LRUBaseLinkedList(); 
        Scanner sc = new Scanner(System.in); 
        while (true) { 
            list.add(sc.nextInt()); 
            list.printAll(); 
        } 
    } 
} 

這段代碼不管緩存有沒有滿，都需要遍歷一遍鏈表，所以這種基于鏈表的實現思路，緩存訪問的時間復雜度為 O(n)。

3.2使用哈希表優化LRU

事實上，這個思路還可以繼續優化，我們可以把單鏈表換成雙向鏈表，并引入散列表。

• 雙向鏈表支持查找前驅，保證操作的時間復雜度為O(1)
• 引入散列表記錄每個數據的位置，將緩存訪問的時間復雜度降到O(1)

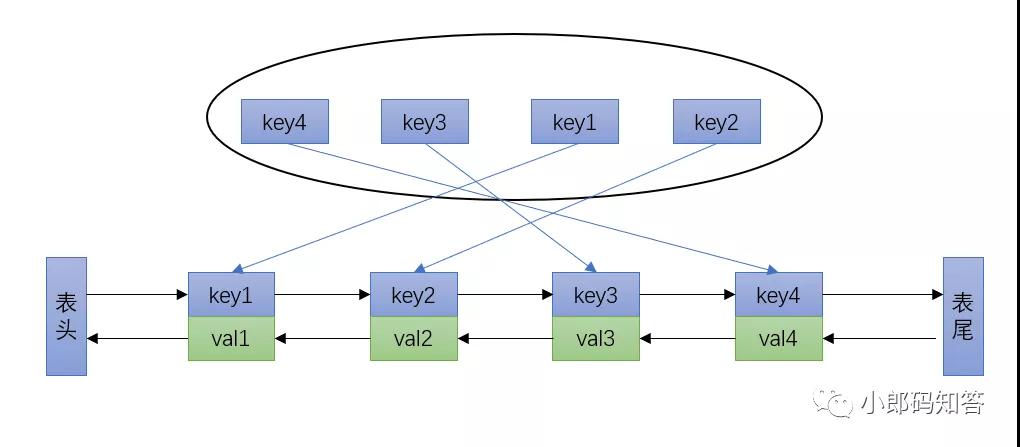
哈希表查找較快，但是數據無固定的順序;鏈表倒是有順序之分。插入、刪除較快，但是查找較慢。將它們結合，就可以形成一種新的數據結構--哈希鏈表(LinkedHashMap)

哈希表+雙向鏈表

力扣上146題-LRU緩存機制剛好可以拿來練手，題圖如下：

題目：

運用你所掌握的數據結構，設計和實現一個 LRU (最近最少使用) 緩存機制 。

• 實現 LRUCache 類：

LRUCache(int capacity) 以正整數作為容量 capacity 初始化 LRU 緩存

int get(int key) 如果關鍵字 key 存在于緩存中，則返回關鍵字的值，否則返回 -1 。

void put(int key, int value) 如果關鍵字已經存在，則變更其數據值;如果關鍵字不存在，則插入該組「關鍵字-值」。當緩存容量達到上限時，它應該在寫入新數據之前刪除最久未使用的數據值，從而為新的數據值留出空間。

思路：

我們的思路就是哈希表+雙向鏈表

• 哈希表用于滿足題目時間復雜度O(1)的要求，雙向鏈表用于存儲順序
• 哈希表鍵值類型：
• 雙向鏈表的節點中除了value外還需要包含key，因為在刪除最久未使用的數據時，需要通過鏈表來定位hashmap中應當刪除的鍵值對
• 一些操作：雙向鏈表中，在后面的節點表示被最近訪問
  • 新加入的節點放在鏈表末尾，addNodeToLast(node)
  • 若容量達到上限，去除最久未使用的數據，removeNode(head.next)
  • 若數據新被訪問過，比如被get了或被put了新值，把該節點挪到鏈表末尾，moveNodeToLast(node)
• 為了操作的方便，在雙向鏈表頭和尾分別定義一個head和tail節點。

代碼

class LRUCache { 
    private int capacity; 
    private HashMap<Integer, ListNode> hashmap;  
    private ListNode head; 
    private ListNode tail; 
 
    private class ListNode{ 
        int key; 
        int val; 
        ListNode prev; 
        ListNode next; 
        public ListNode(){   
        } 
        public ListNode(int key, int val){ 
            this.key = key; 
            this.val = val; 
        } 
    } 
 
    public LRUCache(int capacity) { 
        this.capacity = capacity; 
        hashmap = new HashMap<>(); 
        head = new ListNode(); 
        tail = new ListNode(); 
        head.next = tail; 
        tail.prev = head; 
    } 
 
    private void removeNode(ListNode node){ 
        node.prev.next = node.next; 
        node.next.prev = node.prev; 
    } 
 
    private void addNodeToLast(ListNode node){ 
        node.prev = tail.prev; 
        node.prev.next = node; 
        node.next = tail; 
        tail.prev= node; 
    } 
 
    private void moveNodeToLast(ListNode node){ 
        removeNode(node); 
        addNodeToLast(node); 
    } 
     
    public int get(int key) {    
        if(hashmap.containsKey(key)){ 
            ListNode node = hashmap.get(key); 
            moveNodeToLast(node); 
            return node.val; 
        }else{ 
            return -1; 
        } 
    } 
     
    public void put(int key, int value) { 
        if(hashmap.containsKey(key)){ 
            ListNode node = hashmap.get(key); 
            node.val = value; 
            moveNodeToLast(node); 
            return; 
        } 
        if(hashmap.size() == capacity){ 
            hashmap.remove(head.next.key); 
            removeNode(head.next); 
        } 
 
        ListNode node = new ListNode(key, value); 
        hashmap.put(key, node); 
        addNodeToLast(node); 
    } 
} 

巨人的肩旁：

[1]數據結構與算法之美-王爭

[2]力扣-LRU緩存機制(146題)

[3]https://blog.csdn.net/yangpl_tale/article/details/44998423

[4]https://leetcode-cn.com/problems/lru-cache/solution/146-lru-huan-cun-ji-zhi-ha-xi-biao-shuan-l3um/