[[385574]]

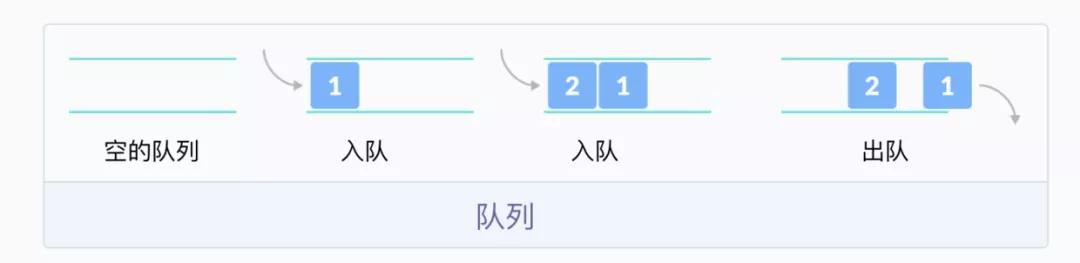
今天繼續來給大家上一盤硬菜，保證喂個半飽——嗝。和棧一樣，隊列(queue)也是一個非常有用的數據結構。同時又非常特殊，它只允許在隊尾(rear)插入元素，在隊首(front)刪除元素，也就是一端進，一端出。

在網上購票普及之前，我們大多數人需要到車站的購票大廳買票，經常是排隊排到水泄不通，queue 就和現實中的排隊是一模一樣的，排在隊首的先買到票，然后離開，緊跟著的人移動到隊首，直到隊列消失。

隊列遵循的是 First In First Out，縮寫為 FIFO，也就是先進先出，第一個進入隊列的第一個先出來。

在上面這幅圖中，1 比 2 先進入隊列，也比 2 先出隊列，規規矩矩的。

對于隊列這樣一個數據結構來說，它有兩個常見的動作：

• enqueue，我個人喜歡把它譯作入隊，指的是把元素放入隊列這個動作。
• dequeue，出隊，指的是把元素從隊列中移除這個動作。

明白了隊列的基本操作后，我們來深入地思考一下，隊列是如何工作的。

1) 建立順序的隊列結構需要為其靜態分配或者動態申請一串連續的存儲空間。

2)然后設置兩個指針進行管理：一個隊首指針 FRONT，指向隊首的元素，一個隊尾指針 REAR，指向隊尾的元素。初始化的時候，FRONT 和 REAR 都設置為 -1。

3)入隊時

檢查隊列是否已經滿了，需要一個 isFull() 的方法來判斷;

對于第一個元素，設置 FRONT 的值為 0;

每次在隊尾插入一個元素時，REAR 加 1，然后把隊尾的元素指向 REAR。

4)出隊時

檢查隊列是否為空，需要一個 isEmpty() 的方法來判斷;

用一個臨時變量來保存隊首的元素，以便出隊后返回;

每次在隊首刪除一個元素時，FRONT 加 1;

如果是最后一個元素，重置 FRONT 和 REAR 為 -1。

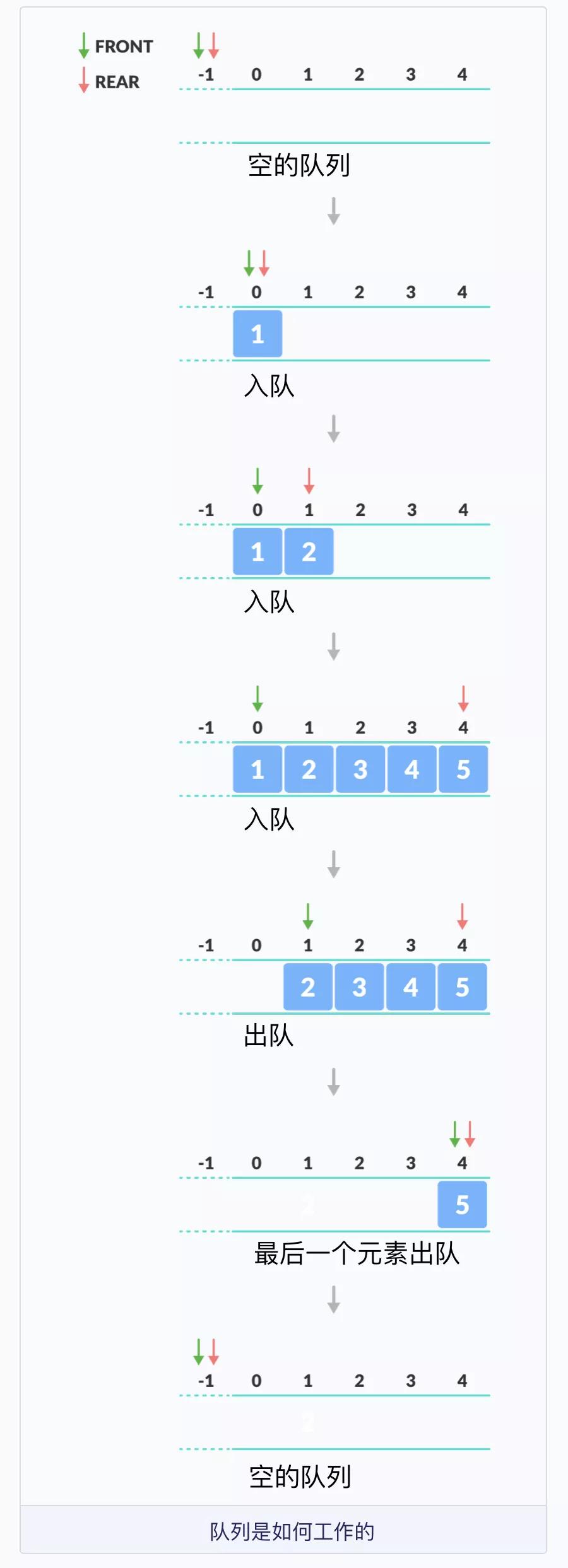
隊列為空的時候，FRONT 和 REAR 等于 -1;把元素 1 入隊的時候，FRONT 變為 1，REAR 加 1 變為 0，queue[FRONT]=queue[REAR] 為 1;把元素 2 入隊的時候，REAR 加 1 變為 1，queue[REAR] 為 2，queue[FRONT] 仍然為 1;接著，元素 3 入隊;元素 4 入隊;元素 5 入隊，REAR 變為 4，queue[REAR] 為 5，queue[FRONT] 仍然為 1。

元素 1 出隊的時候，FRONT 為 0，queue[FRONT] 為 1，然后 FRONT 加 1 變為 1;元素 2 出隊的時候，queue[FRONT] 為 2，然后 FRONT 加 1 變為 2;接著，元素 3 出隊;元素 4 出隊;元素 5 出隊的時候，queue[FRONT] 為 5，FRONT 為 4，REAR 為 4，出隊后，FRONT 和 REAR 重設為 -1。

假設隊列中的元素為 int 類型，隊列的大小為 5，我們可以用 Java 語言來自定義一個最簡單的 queue。它需要 3 個字段：

• int queue[]，一個 int 類型的數組，來存放數據
• int front，一個 int 類型的隊首標記
• int rear，一個 int 類型的隊尾標記

class Queue { 
    int SIZE = 5; 
    int items[] = new int[SIZE]; 
    int front, rear; 
} 

初始化隊列：

Queue() { 
    front = -1; 
    rear = -1; 
} 

入隊：

void enQueue(int element) { 
    if (isFull()) { 
        System.out.println("隊列已經滿了"); 
    } else { 
        if (front == -1) 
            front = 0; 
        rear++; 
        items[rear] = element; 
        System.out.println("插入 " + element); 
    } 
} 

出隊：

int deQueue() { 
    int element; 
    if (isEmpty()) { 
        System.out.println("隊列空了"); 
        return (-1); 
    } else { 
        element = items[front]; 
        if (front >= rear) { 
            front = -1; 
            rear = -1; 
        } 
        else { 
            front++; 
        } 
        System.out.println("刪除 -> " + element); 
        return (element); 
    } 
} 

檢查隊列是否已經滿了：

boolean isFull() { 
    if (front == 0 && rear == SIZE - 1) { 
        return true; 
    } 
    return false; 
} 

檢查隊列是否為空：

boolean isEmpty() { 
    if (front == -1) 
        return true; 
    else 
        return false; 
} 

來個 main() 方法測試下：

void display() { 
    int i; 
    if (isEmpty()) { 
        System.out.println("隊列為空"); 
    } else { 
        System.out.println("\n隊首的下標-> " + front); 
        System.out.println("元素 -> "); 
        for (i = front; i <= rear; i++) 
            System.out.print(items[i] + "  "); 
 
        System.out.println("\n隊尾的下標-> " + rear); 
    } 
} 
 
public static void main(String[] args) { 
    Queue q = new Queue(); 
 
    // 隊列為空的時候不允許出隊 
    q.deQueue(); 
 
    // enQueue 5 elements 
    q.enQueue(1); 
    q.enQueue(2); 
    q.enQueue(3); 
    q.enQueue(4); 
    q.enQueue(5); 
 
    // 隊列滿了的時候不允許入隊 
    q.enQueue(6); 
 
    q.display(); 
 
    // 出隊 
    q.deQueue(); 
 
    // 打印 
    q.display(); 
} 

打印結果如下所示：

隊列空了 
插入 1 
插入 2 
插入 3 
插入 4 
插入 5 
隊列已經滿了 
 
隊首的下標-> 0 
元素 ->  
1  2  3  4  5   
隊尾的下標-> 4 
刪除 -> 1 
 
隊首的下標-> 1 
元素 ->  
2  3  4  5   
隊尾的下標-> 4 

隊列空了插入 1插入 2插入 3插入 4插入 5隊列已經滿了隊首的下標-> 0元素 -> 1 2 3 4 5 隊尾的下標-> 4刪除 -> 1隊首的下標-> 1元素 -> 2 3 4 5 隊尾的下標-> 4

好了，這種基本的隊列已經可以正常工作了，但它有一個問題：當已經出隊了 N 個元素后，按理說，應該可以再入隊 N 個元素，對吧?因為省出來了 N 個空間嘛。

Queue q = new Queue(); 
 
// enQueue 5 elements 
q.enQueue(1); 
q.enQueue(2); 
q.enQueue(3); 
q.enQueue(4); 
q.enQueue(5); 
 
// 出隊 
q.deQueue(); 
q.deQueue(); 
 
q.enQueue(6); 
q.enQueue(7); 

但事實上，這段代碼在運行的時候報錯了：

插入 1 
插入 2 
插入 3 
插入 4 
插入 5 
刪除 -> 1 
刪除 -> 2 
Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException: Index 5 out of bounds for length 5 
 at com.itwanger.queue.Queue.enQueue(Queue.java:23) 
 at com.itwanger.queue.Queue.main(Queue.java:89) 

看見 ArrayIndexOutOfBoundsException 我們就知道，數組越界了。這是因為我們是用數組實現的隊列，在出隊的時候 REAR 并沒有減小，導致入隊的時候 items[rear++]超出了數組的邊界。

可以把問題歸咎于我們實現隊列的方式上，也可以淺顯地認為基本類型的隊列存在有局限性。隨著入隊和出隊的連續操作，隊列中的元素在不停地變化，隊列所占的存儲空間也在分配的連續空間中不停的移動。

當 REAR 增加到超出數組大小的范圍之后，隊列就無法添加新的元素了，事實上還有很多空間可以利用，但它們仍然被已出隊的元素占用著——正所謂“附身”啊。除非所有的元素均被移除后， FRONT 和 REAR 被重置，隊列才能重新使用。

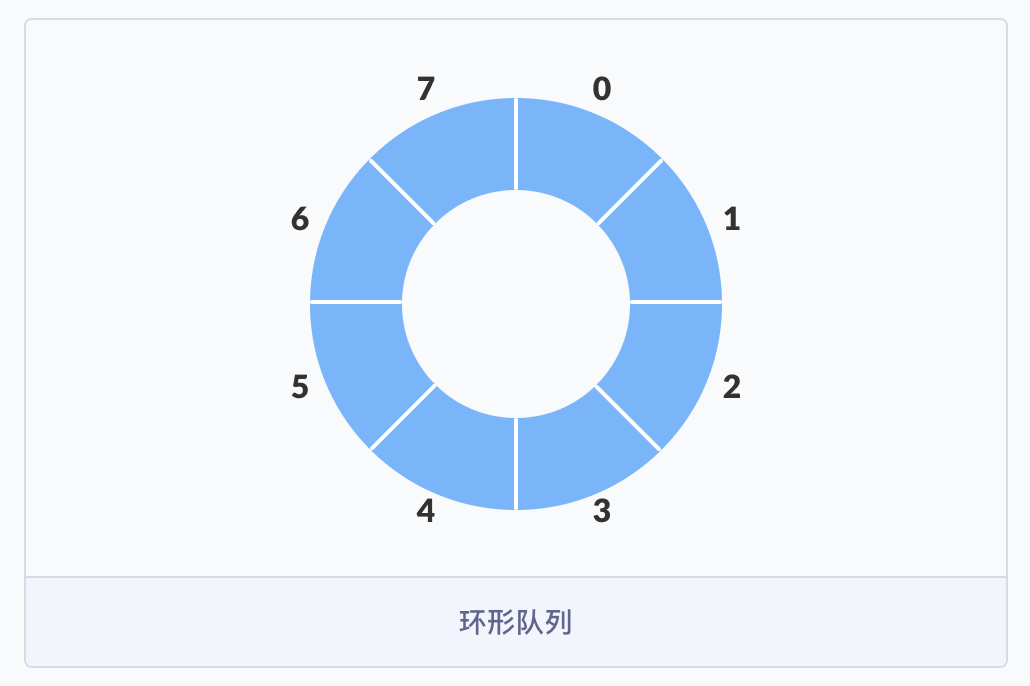
由于基本類型的隊列存在這種局限性，我們就迫切的需要一種新型隊列的出現——環形隊列(Circular queue) 就閃亮登場了。

那環形隊列是如何工作的呢?它是怎么解決這個問題的呢?

1)同樣需要一串連續的存儲空間。

2)初始化的時候和基本類型的隊列 完全一樣;

3)入隊時

• 檢查隊列是否已經滿了，此時的條件除了 FRONT = 0 && REAR = SIZE + 1， 也就是隊首有元素，隊尾也有元素時，也就是第一次把隊列填滿時。還需要再增加一個：FRONT = REAR + 1，也就是隊尾緊跟在隊首后面的時候，循環把隊列填滿時。代碼如下所示。

boolean isFull() { 
    if (front == 0 && rear == SIZE - 1) { 
        return true; 
    } 
     
    if (front == rear + 1) { 
        return true; 
    } 
    return false; 
} 

• 一旦 REAR 加 1 后超出了所分配的連續空間，就讓它指向連續空間的起始位置。也就是說，REAR 需要重新輪循了，從 0 開始，可以用 (REAR + 1) % SIZE 取余的形式來表示。代碼如下所示。

void enQueue(int element) { 
    if (isFull()) { 
        System.out.println("隊列已經滿了"); 
    } else { 
        if (front == -1) 
            front = 0; 
        rear = (rear + 1) % SIZE; 
        items[rear] = element; 
        System.out.println("插入 " + element); 
    } 
} 

4)出隊時

• 同樣的，當 FRONT 加 1 超出了所分配的連續空間，就讓它指向連續空間的起始位置。也就是說，FRONT 需要重新輪循了，從 0 開始，可以用 (FRONT + 1) % SIZE 來表示。代碼如下所示。

int deQueue() { 
    int element; 
    if (isEmpty()) { 
        System.out.println("隊列空了"); 
        return (-1); 
    } else { 
        element = items[front]; 
        if (front >= rear) { 
            front = -1; 
            rear = -1; 
        } 
        else { 
            front = (front + 1) % SIZE; 
        } 
        System.out.println("刪除 -> " + element); 
        return (element); 
    } 
} 

main() 方法的測試代碼就不再貼了，和基本類型的隊列時差別不大。一圖勝千言，我們來畫一幅圖表示下環形隊列的工作方式。

當隊列第一次被填滿了以后，出隊了兩個元素，此時下標為 0 和 1 的兩個位置空了出來，然后入隊元素 6，意味著 6 變成了隊尾，也就是 REAR 等于 0 了;再入隊元素 7，7 變成了隊尾，也就是 REAR 等于 1 了。

現在，來思考一個問題，假如此時執行 deQueue() 方法出隊一個元素時，哪一個元素會被移除呢?答案是元素 3，因為此時它在隊首，之后是元素 4，元素 5，元素 6，元素 7，雖然直觀上看起來不是那么回事，但如果把它想象成一個環形的而不是直線型的就很好理解了。

對比來說，環形隊列比普通類型的隊列在容量的利用上更充分一點。

除了基本類型和環形隊列之外，隊列還有優先級隊列和雙端隊列，雖然它們都歸到了隊列這一類，但其實并不遵循 FIFO 的規則，所以我就打算把它們拎出來單獨來講。

本文轉載自微信公眾號「 沉默王二」，可以通過以下二維碼關注。轉載本文請聯系 沉默王二公眾號。