提到回歸算法，我想很多人都會想起線性回歸，因為它通俗易懂且非常簡單。但是，線性回歸由于其基本功能和有限的移動自由度，通常不適用于現實世界的數據。

實際上，它只是經常用作評估和研究新方法時進行比較的基準模型。在現實場景中我們經常遇到回歸預測問題，今天我就給大家總結分享 5 種回歸算法。

1、神經網絡回歸

理論

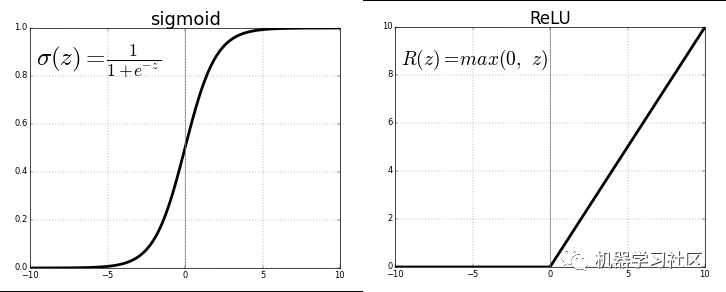
神經網絡的強大令人難以置信的，但它們通常用于分類。信號通過神經元層，并被概括為幾個類。但是，通過更改最后的激活功能，它們可以非常快速地適應回歸模型。

每個神經元通過激活功能傳遞以前連接的值，達到泛化和非線性的目的。常用的激活函數：Sigmoid 或 ReLU 函數。

通過將最后一個激活函數(輸出神經元)替換為線性激活函數，可以將輸出映射到固定類別之外的各種值。這樣，輸出不是將輸入分類到任何一個類別中的可能性，而是神經網絡將觀測值置于其上的連續值。從這個意義上講，它就像是線性回歸的神經網絡的補充。

神經網絡回歸具有非線性(除了復雜性)的優點，可以在神經網絡中較早地通過S型和其他非線性激活函數引入神經網絡。但是，由于 ReLU 忽略了負值之間的相對差異，因此過度使用 ReLU 作為激活函數可能意味著該模型傾向于避免輸出負值。這可以通過限制 ReLU 的使用并添加更多的負值適當的激活函數來解決，也可以通過在訓練之前將數據標準化為嚴格的正范圍來解決。

實現

使用Keras，我們構建了以下人工神經網絡結構，只要最后一層是具有線性激活層的密集層或簡單地是線性激活層即可。

model = Sequential() 
model.add(Dense(100, input_dim=3, activation='sigmoid')) 
model.add(ReLU(alpha=1.0)) 
model.add(Dense(50, activation='sigmoid')) 
model.add(ReLU(alpha=1.0)) 
model.add(Dense(25, activation='softmax')) 
#IMPORTANT PART 
model.add(Dense(1, activation='linear')) 

神經網絡的問題一直是其高方差和過度擬合的趨勢。在上面的代碼示例中，有許多非線性源，例如SoftMax或Sigmoid。如果你的神經網絡在純線性結構的訓練數據上表現良好，則最好使用修剪后的決策樹回歸法，該方法可以模擬神經網絡的線性和高變異性，但可以讓數據科學家更好地控制深度、寬度和其他屬性以控制過度擬合。

2、決策樹回歸

理論

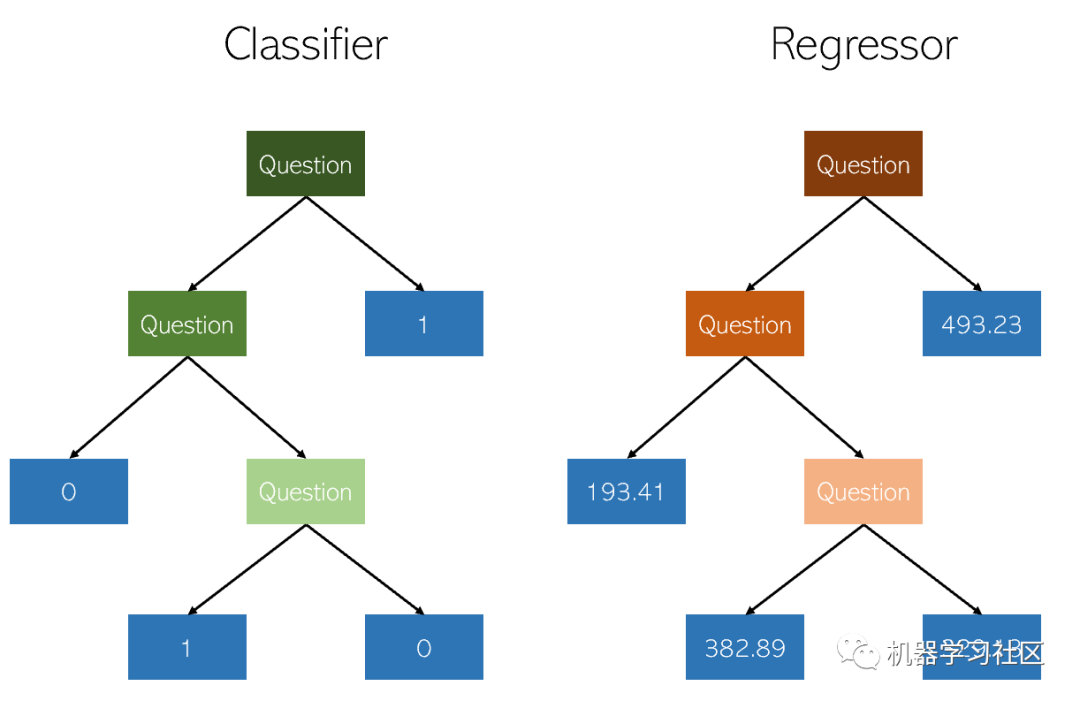
在決策樹中分類和回歸非常相似，因為兩者都通過構造是/否節點的樹來工作。雖然分類結束節點導致單個類值(例如，對于二進制分類問題為1或0)，但是回歸樹以連續值(例如4593.49或10.98)結尾。

由于回歸作為機器學習任務的特殊性和高差異性，因此需要仔細修剪決策樹回歸器。但是，它進行回歸的方式是不規則的，而不是連續地計算值。因此，應該修剪決策樹，使其具有最大的自由度。

實現

決策樹回歸可以很容易地在 sklearn 創建：

from sklearn.tree import DecisionTreeRegressor 
model = DecisionTreeRegressor() 
model.fit(X_train, y_train) 

由于決策樹回歸參數非常重要，因此建議使用sklearn的GridCV參數搜索優化工具來找到模型的正確準則。在正式評估性能時，請使用K折檢驗而不是標準的訓練分割，以避免后者的隨機性干擾高方差模型的精細結果。

3、LASSO 回歸

理論

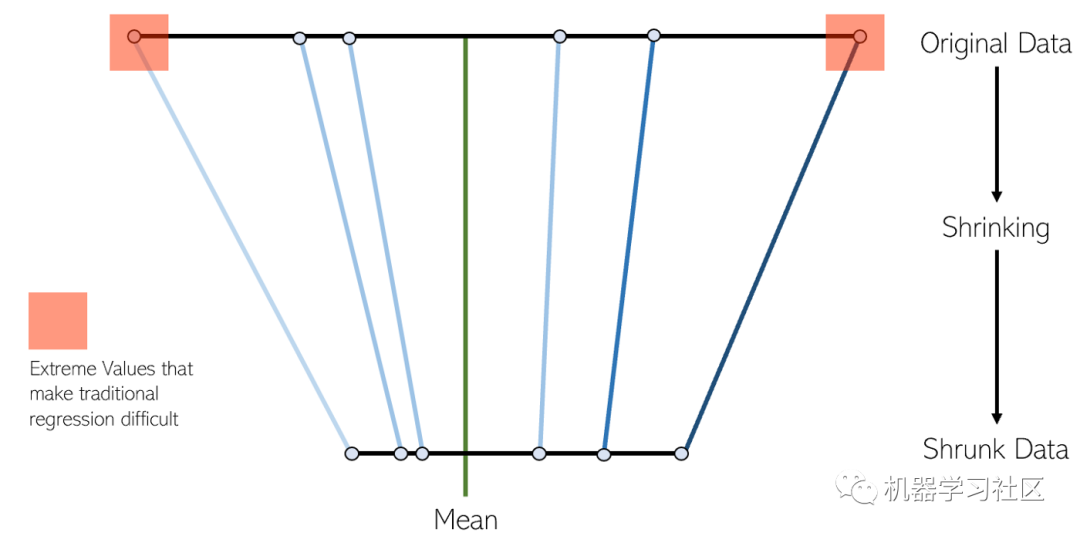
LASSO回歸是線性回歸的一種變體，特別適合于多重共線性(要素彼此之間具有很強的相關性)的數據。它可以自動執行部分模型選擇，例如變量選擇或參數消除。

縮小的過程為回歸模型增加了許多好處：

• 對真實參數的估計更加準確和穩定。
• 減少采樣和非采樣錯誤。
• 空間波動更平滑。

LASSO并沒有像神經網絡的高方差方法和決策樹回歸那樣通過調整模型的復雜性來補償數據的復雜性，而是試圖通過變形空間來降低數據的復雜性，從而能夠通過簡單的回歸技術來處理。在此過程中，LASSO自動以低方差方法幫助消除或扭曲高度相關和冗余的特征。

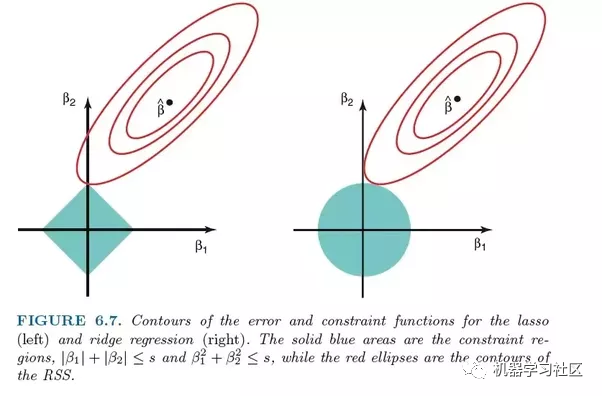
LASSO回歸使用L1正則化，這意味著它按絕對值加權誤差。這種正則化通常會導致具有較少系數的稀疏模型，這使得它具有可解釋性。

實現

在sklearn中，LASSO回歸附帶了一個交叉驗證模型，該模型可以選擇許多具有不同基本參數和訓練路徑的訓練模型中表現最佳的模型，從而使需要手動完成的任務實現自動化。

from sklearn.linear_model import LassoCV 
model = LassoCV() 
model.fit(X_train, y_train) 

4、Ridge回歸

理論

Ridge回歸與LASSO回歸非常相似，因為它適用于收縮。Ridge和LASSO回歸都非常適用于具有大量彼此不獨立(共線性)的特征的數據集，但是兩者之間最大的區別是Ridge利用L2正則化，由于L2正則化的性質，系數越來越接近零，但是無法達到零。

正因為如此，如果你希望對每個變量的優先級產生小的影響進行優先級排序，則 Ridge 是更好的選擇。如果希望在模型中考慮幾個變量，每個變量具有中等到較大的影響，則 LASSO 是更好的選擇。

實現

Ridge回歸可以在sklearn中實現，如下所示。像 LASSO 回歸一樣，sklearn可以實現交叉驗證選擇許多受過訓練的模型中最好的模型的實現。

from sklearn.linear_model import RidgeCV 
model = Ridge() 
model.fit(X_train, y_train) 

5、ElasticNet 回歸

理論

ElasticNet 試圖通過結合L1和L2正則化來利用 Ridge 回歸和 LASSOb回歸中的最佳方法。

LASSO和Ridge提出了兩種不同的正則化方法。λ是控制懲罰強度的轉折因子。

• 如果λ= 0，則目標變得類似于簡單線性回歸，從而獲得與簡單線性回歸相同的系數。
• 如果λ=∞，則由于系數平方的權重無限大，系數將為零。小于零的值會使目標無限。
• 如果0 <λ<∞，則λ的大小決定賦予物鏡不同部分的權重。

除了λ參數之外，ElasticNet還添加了一個附加參數α，用于衡量L1和L2正則化應該如何"混合":

• 當α等于0時，該模型是純粹的嶺回歸模型，
• 而當α等于1時，它是純粹的LASSO回歸模型。

“混合因子”α只是確定在損失函數中應考慮多少L1和L2正則化。

實現

可以使用 sklearn 的交叉驗證模型來實現ElasticNet：

from sklearn.linear_model import ElasticNetCV 
model = ElasticNetCV() 
model.fit(X_train, y_train)