原以為哈夫曼樹、哈夫曼編碼很難,結果……
哈夫曼樹介紹
大家好,我是bigsai。原以為哈夫曼樹、哈夫曼編碼很難,結果它很簡單啊老鐵們!
哈夫曼樹、哈夫曼編碼很多人可能聽過,但是可能并沒有認真學習了解,今天這篇就比較詳細的講一下哈夫曼樹。
首先哈夫曼樹是什么?
哈夫曼樹的定義:給定N個權值作為N個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(Huffman Tree),哈夫曼樹是帶權路徑長度最短的樹。權值較大的結點離根較近。
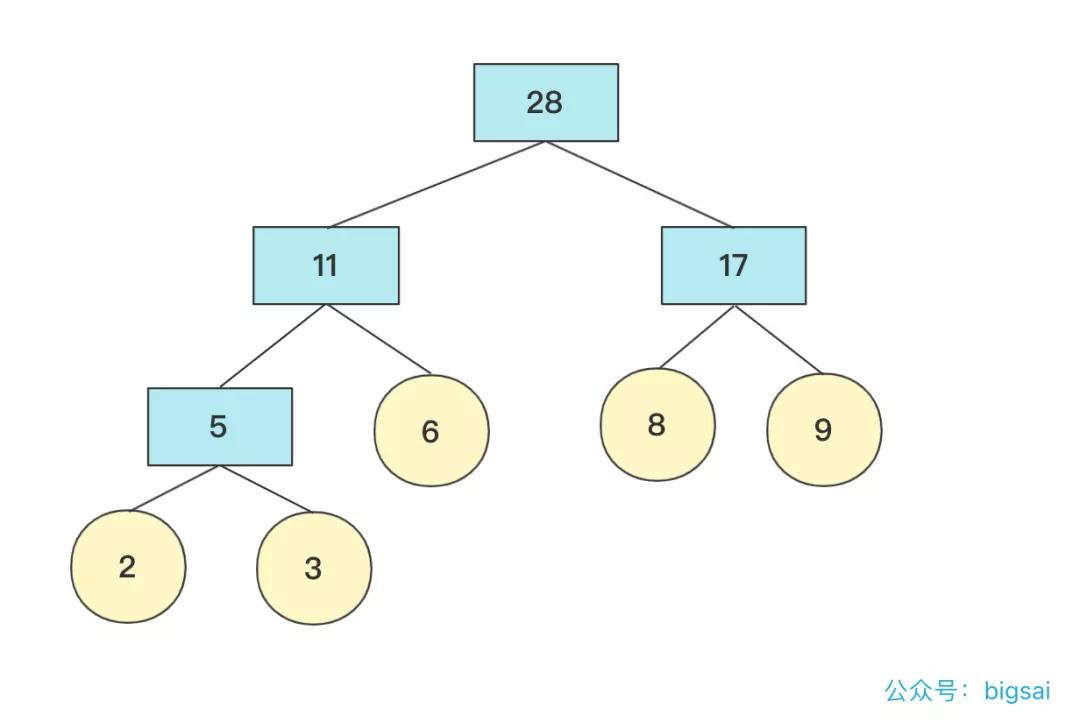
那這個樹長啥樣子呢?例如開始2,3,6,8,9權值節點構成的哈夫曼樹是這樣的:
從定義和圖上你也可以發現下面的規律:
- 初始節點都在樹的葉子節點上
- 權值大的節點離根更近
- 每個非葉子節點都有兩個孩子(因為我們自下向上構造,兩個孩子構成一個新樹的根節點)
你可能會好奇這么一個哈夫曼樹是怎么構造的,其實它是按照一個貪心思想和規則構造,而構造出來的這個樹的權值最小。這個規則下面會具體講解。
哈夫曼樹非常重要的一點:WPL(樹的所有葉結點的帶權路徑長度之和)。至于為什么按照哈夫曼樹方法構造得到的權重最小,這里不進行證明,但是你從局部來看(三個節點)也要權值大的在上一層WPL才更低。
WPL計算方法: WPL=求和(Wi * Li)其中Wi是第i個節點的權值(value)。Li是第i個節點的長(深)度.
例如上面 2,3,6,8,9權值節點構成的哈夫曼樹的WPL計算為(設根為第0層):
比如上述哈夫曼樹的WPL為:2*3+3*3+6*2+8*2+9*2=(2+3)*3+(6+8+9)*2=61.
既然了解了哈夫曼樹的一些概念和WPL的計算方式,下面看看哈夫曼樹的具體構造方式吧!
哈夫曼樹構造
初始給一個森林有n個節點。我們主要使用貪心的思想來完成哈夫曼樹的構造:
- 在n個節點找到兩個最小權值節點(根),兩個為葉子結構構建一棵新樹(根節點權值為左右孩子權值和)
- 先刪掉兩個最小節點(n-2)個,然后加入構建的新節點(n-1)個
- 重復上面操作,一直到所有節點都被處理
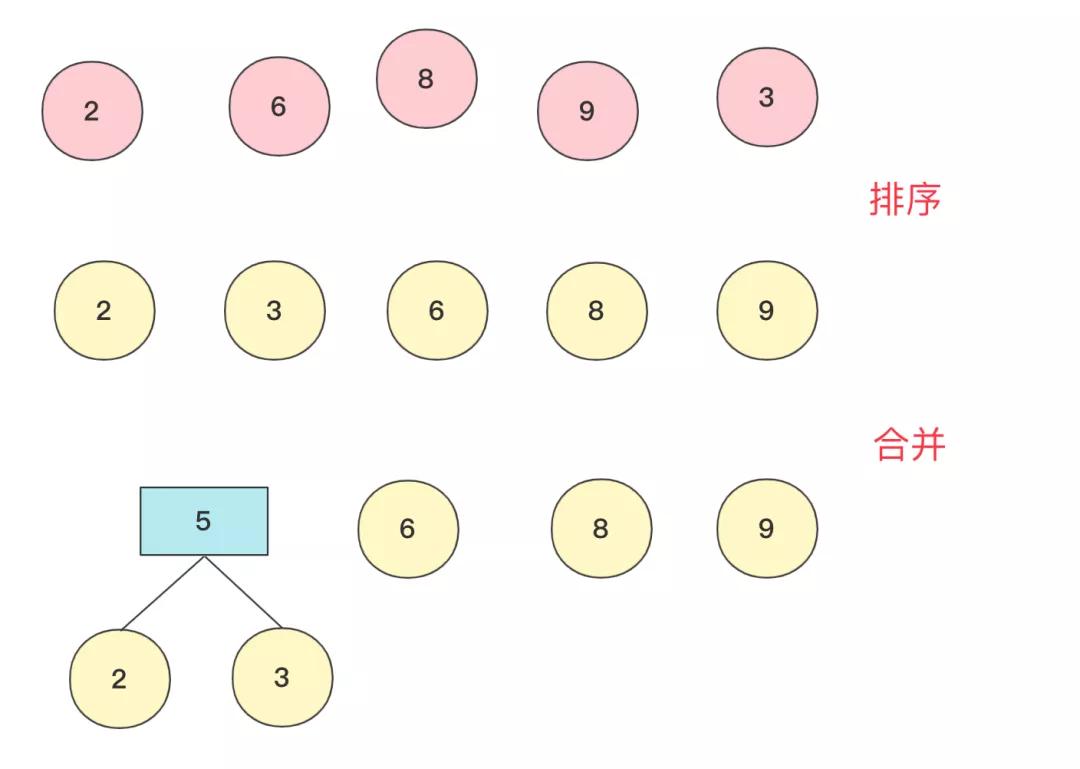
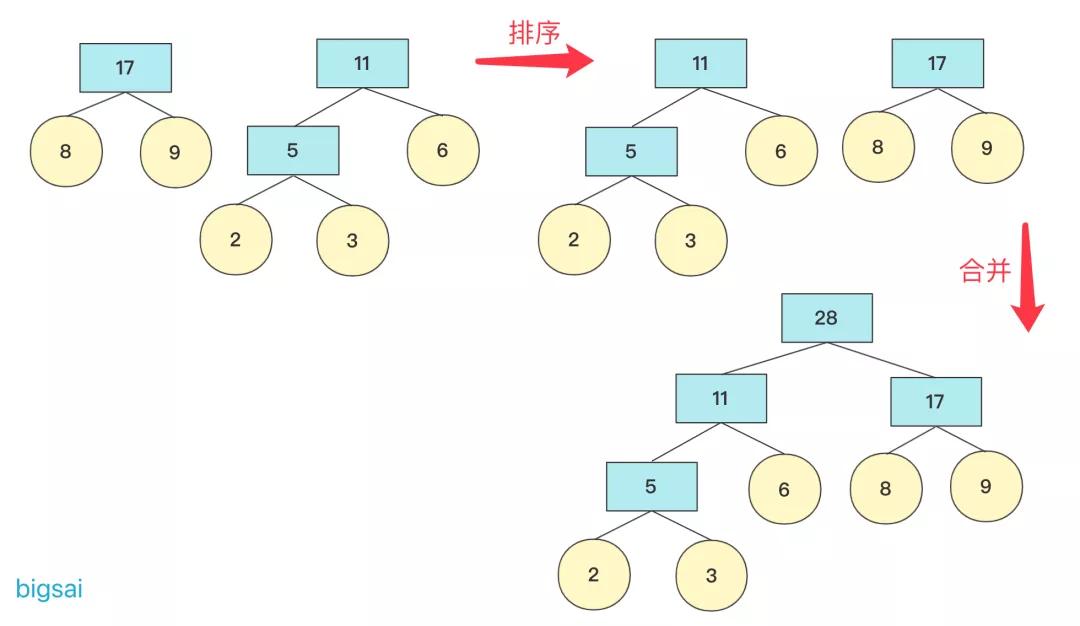
在具體實現上,找到最小兩個節點需要排序操作,我們來看看2,6,8,9,3權值節點構成哈夫曼樹的過程。
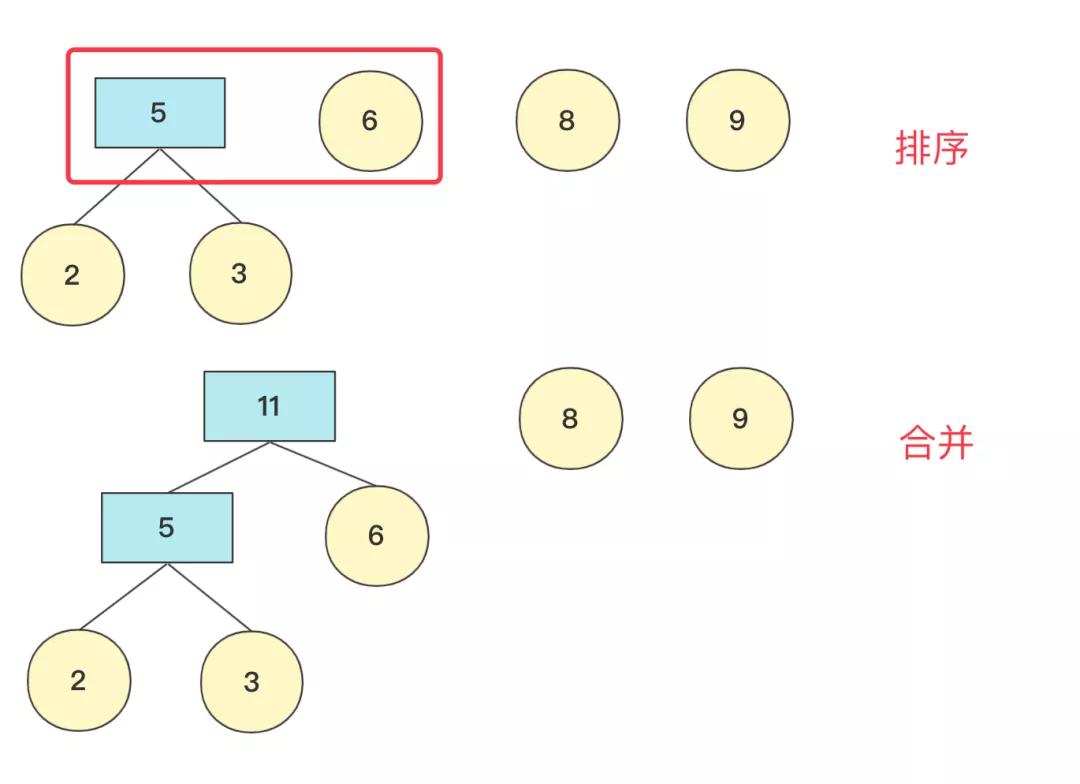
初始時候各個節點獨立,先將其排序(這里使用優先隊列),然后選兩個最小節點(拋出)生成一個新的節點,再將其加入優先隊列中,此次操作完成后優先隊列中有5,6,8,9節點
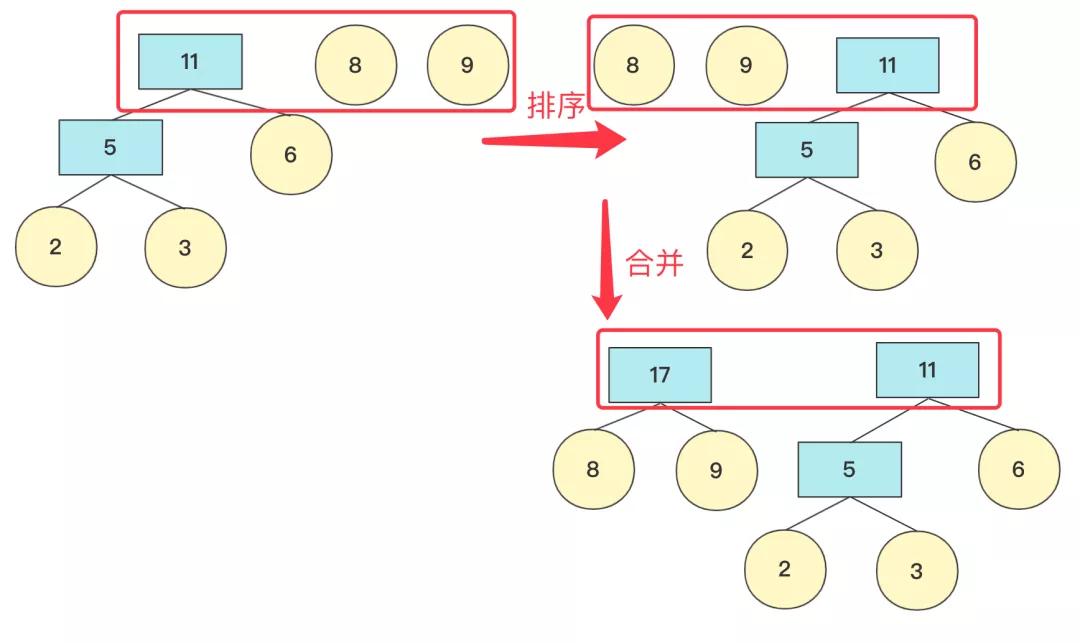
重復上面操作,這次結束 隊列中有11,8,9節點(排序后8,9,11)
圖片如果隊列為空,那么返回節點,并且這個節點為整個哈夫曼樹根節點root。
否則繼續加入隊列進行排序。重復上述操作,直到隊列為空。
在計算帶權路徑長度WPL的時候,需要重新計算高度(從下往上),因為哈夫曼樹是從下往上構造的,并沒有以常量維護高度,可以構造好然后計算高度。
具體代碼實現(僅供參考)
- import java.util.ArrayDeque;
- import java.util.ArrayList;
- import java.util.Comparator;
- import java.util.List;
- import java.util.PriorityQueue;
- import java.util.Queue;
- public class HuffmanTree {
- public static class node
- {
- int value;
- node left;
- node right;
- int deep;//記錄深度
- public node(int value) {
- this.value=value;
- this.deep=0;
- }
- public node(node n1, node n2, int value) {
- this.left=n1;
- this.right=n2;
- this.value=value;
- }
- }
- private node root;//最后生成的根節點
- List<node>nodes;
- public HuffmanTree() {
- this.nodes=null;
- }
- public HuffmanTree(List<node>nodes)
- {
- this.nodes=nodes;
- }
- public void createTree() {
- Queue<node>q1=new PriorityQueue<node>(new Comparator<node>() {
- public int compare(node o1, node o2) {
- return o1.value-o2.value;
- }});
- q1.addAll(nodes);
- while(!q1.isEmpty()){
- node n1=q1.poll();
- node n2=q1.poll();
- node parent=new node(n1,n2,n1.value+n2.value);
- if(q1.isEmpty()){
- root=parent;return;
- }
- q1.add(parent);
- }
- }
- public int getweight() {
- Queue<node>q1=new ArrayDeque<node>();
- q1.add(root);
- int weight=0;
- while (!q1.isEmpty()) {
- node va=q1.poll();
- if(va.left!=null){
- va.left.deep=va.deep+1;va.right.deep=va.deep+1;
- q1.add(va.left);q1.add(va.right);
- }
- else {
- weight+=va.deep*va.value;
- }
- }
- return weight;
- }
- public static void main(String[] args) {
- List<node>list=new ArrayList<node>();
- list.add(new node(2));
- list.add(new node(3));
- list.add(new node(6));
- list.add(new node(8));list.add(new node(9));
- HuffmanTree tree=new HuffmanTree();
- tree.nodes=list;
- tree.createTree();
- System.out.println(tree.getweight());
- }
- }
輸出結果:
- 61
哈夫曼編碼
除了哈夫曼樹你聽過,哈夫曼編碼你可能也聽過,但是不一定了解它是個什么玩意兒,哈夫曼編碼其實就是哈夫曼樹的一個非常重要的應用,在這里就簡單介紹原理并不詳細實現了。
哈夫曼編碼定義:哈夫曼編碼(Huffman Coding),又稱霍夫曼編碼,是一種編碼方式,哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman于1952年提出一種編碼方法,該方法完全依據字符出現概率來構造異字頭的平均長度最短的碼字,有時稱之為最佳編碼,一般就叫做Huffman編碼(有時也稱為霍夫曼編碼)。
哈夫曼編碼的目的是為了減少存儲體積,以一個連續的字符串為例,拋開編程語言中實際存儲,就拿
aaaaaaaaaabbbbbcccdde
這個字符串來說,在計算機中如果每個字符都是定長存儲(假設長為4的二進制存儲),計算機只知道0和1的二進制,假設
- a:0001
- b:0010
- c:0011
- d:0100
- e:0101
那么上面字符串可以用二進制存儲是這樣的
000100010001000100010001……0101
如果每個字符編碼等長,那么就沒有存儲空間優化可言,都是單個字符長度 * 字符個數。但是如果每個字符編碼不等長,那么設計的開放性就很強了。
比如一個字符串aaaaabb
如果設計a為01,b設計為1。那么二進制就為:010101010111
如果設計a為1,b設計為01。那么二進制就為:111110101
如果設計a為1,b設計為0。那么二進制就為:1111100
你看,在計算機的01二進制世界中,明顯第二種比第一種優先,第三種又比第二種優先。所以,設計編碼要考慮讓出現多的盡量更短,出現少的稍微長點沒關系。
但是,你需要考慮的一個問題是,二進制開始0,1,01,10,11這個順序 ,如果來了001它到底是0,0,1還是0,01呢?所以編碼不等長的時候你要考慮到這個編碼要有唯一性不能出現歧義。這個怎么搞呢?
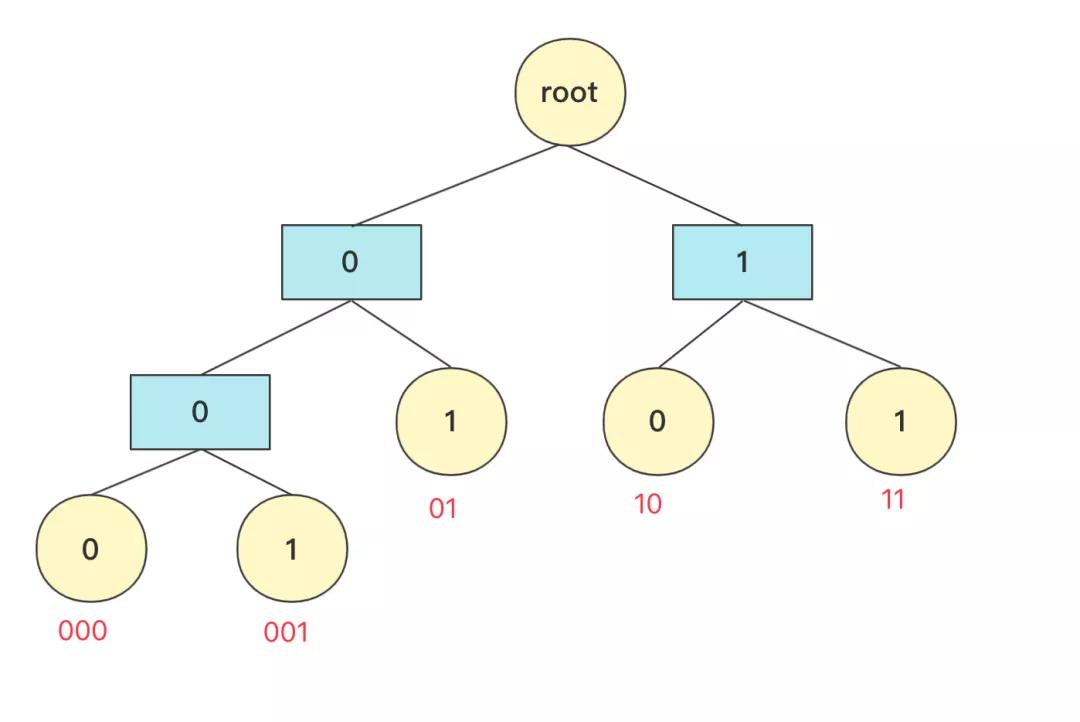
簡單啊,計算機只知道01二進制,而二叉樹剛好有左右兩個節點,至于一個字符它如果是對應葉子節點,那么就可以直接確定,也就是這個數值如果映射成一個二叉樹字符不能存在非葉子節點上。
所以,哈夫曼編碼具體流程就很清晰了,先統計字符出現的次數,然后將這個次數當成權值按照上面介紹的方法構造一棵哈夫曼樹,然后樹的根不存,往左為0往右為1每個葉子節點得到的二進制數字就是它的編碼,這樣頻率高的字符在上面更短在整個二進制存儲中也更節省空間。
結語
哈夫曼樹還是比較容易理解,主要構造利用貪心算法的思想去從下往上構建,哈夫曼編碼相信看了你也有所收獲,有興趣可以自己實現一下哈夫曼編碼的代碼(編碼、解碼)。本人水平有限,如果有錯誤還希望大佬指正!