[[406628]]

虛擬環境（ALE、MuJoCo、OpenAI Gym）極大地促進了在智能體控制和規劃方面學習算法的發展和評估，然而現有的虛擬環境通常只涉及剛體動力學。盡管軟體動力學在多個研究領域有著廣泛的應用（例如，醫療護理中模擬虛擬手術、計算機圖形學中模擬人形角色、機器人技術中開發仿生制動器、材料科學中分析斷裂和撕裂），關于構建標準軟體環境和基準的研究卻很少。

與剛體動力學相比，軟體動力學的模擬、控制和分析更加錯綜復雜。最大的挑戰之一來自其無限的自由度（DoFs）和對應的高維控制方程。軟體動力學的內在復雜性使許多為剛體設計的機器人算法無法直接應用，并抑制了用于評估軟體任務算法的模擬基準的發展。

在一項近期研究中，MIT 沃森人工智能實驗室首席科學家淦創團隊與來自MIT, USCD等機構的研究者共同提出了一個支持梯度可導的機器人軟體操作平臺（PlasticineLab) 來解決這個問題。這篇論文內容在 ICLR 2021 大會上被選為spotlight。

論文地址：
https://arxiv.org/pdf/2104.03311.pdf

項目鏈接：
http://plasticinelab.csail.mit.edu/

Code 下載：
https://github.com/hzaskywalker/PlasticineLab

該基準可用于運行和評估總共 10 種軟體操作任務，這些任務包含 50 種配置，必須通過復雜的操作來執行，包括捏、滾、切、成型和雕刻。其特點在于模擬環境采用可微物理，并且首次為軟體分析提供梯度信息，從而可以通過基于梯度的優化進行監督學習。在軟體模型方面，我們選擇了研究橡皮泥（圖 1 左），這是一種用于雕刻的多功能彈塑性材料，在小變形下表現為彈性形變，在大變形下表現為塑性形變。與常規彈性軟體相比，橡皮泥具有更加多樣和真實的行為，并帶來了先前研究中未探索的挑戰，使其成為測試軟體操作算法的代表性媒介（圖 1 右）。

圖 1 左：一個孩子用搟面杖將一塊橡皮泥變形成薄餅。右：PlasticineLab 中具有挑戰性的 RollingPin 場景。智能體需要通過來回滾動搟面杖，使橡皮泥變形為目標形狀。

我們通過 Taichi 實現 PlasticineLab 的梯度支持和彈塑性材料模型，其 CUDA 后端采用 GPU 大規模并行來實時模擬各種 3D 軟體。隨后通過移動最小二乘材料點法和 von Mises 屈服準則對彈塑性材料進行建模，并利用 Taichi 的雙尺度反向模式微分系統來自動計算梯度，包括塑性材料模型帶來的具有數值挑戰性的 SVD 梯度。具備完整的梯度后，我們在 PlasticineLab 中所有軟體操作任務上評估了基于梯度的規劃算法，并將其效率與基于強化學習的方法進行了比較。

實驗表明，基于梯度的規劃算法可以利用物理模型的額外知識在數十次迭代中找到更有價值的解決方案，而基于強化學習的方法即使在 1 萬次迭代之后仍可能會失敗。但是基于梯度的方法缺乏足夠的動力來解決長期規劃問題，尤其是在多階段任務上。

這些發現加深了對基于強化學習和基于梯度的規劃算法的理解。此外，它還提供了一個可能的研究方向，即融合這兩種方法的優點來推進軟體動力學復雜規劃任務的發展。這項工作主要有以下幾點貢獻：

提出了首個涉及彈性和塑性軟體的技能學習基準。

開發了一個功能齊全的可微物理引擎，它支持彈性和塑性變形、軟剛性材料相互作用，以及可微的定制接觸模型。

基準中廣泛的任務覆蓋范圍能夠對代表性基于強化學習和基于梯度的規劃算法進行系統的評估和分析。我們希望該基準可以激發未來的研究，將可微物理和強化學習相結合。

我們還計劃通過更多的關節系統來擴展基準測試，例如虛擬影子手。作為一種起源于計算物理界的原理性模擬方法，MPM 在細化下可收斂，并且具有自身的精度優勢。建模錯誤在虛擬環境中不可避免，不過，模擬梯度信息除了作為規劃的強大監督信號外，還可以指導系統識別。這可能使機器人學研究人員能夠自己「優化」任務，與控制器優化同時進行，從而自動最小化模擬與真實之間的差距。PlasticineLab 可以顯著降低未來軟體操縱技能學習研究的障礙，并為機器學習社區做出獨特貢獻。

PLASTICINELAB 學習環境

PlasticineLab 包含由可微物理模擬器支持的具有挑戰性的軟體操作任務，其中的所有任務都需要智能體使用剛體操縱器將一塊或多塊 3D 橡皮泥變形。底層模擬器允許用戶對軟體執行復雜的操作，包括捏、滾、切、成型和雕刻。

任務描述

PlasticineLab 具有 10 種側重于軟體操作的任務。每個任務都包含一個或多個軟體和一個操縱器，最終目標是通過規劃操縱器的運動將軟體變形為目標形狀。智能體的設計遵循標準的強化學習框架，通過馬爾可夫決策過程進行建模。每個任務的設計由其狀態和觀察、動作表征、目標定義以及獎勵函數來定義。

馬爾可夫決策過程

一般來說，馬爾可夫決策過程包含狀態空間、動作空間、獎勵函數和轉換函數。在 PlasticineLab 中，物理模擬器決定了狀態之間的轉換。智能體的目標是找到一個隨機策略，根據給定狀態對動作進行采樣，從而最大化預期累積未來回報，其中為折扣因子。

狀態

任務的狀態包括軟體的正確表征和操縱器的末端執行器。我們遵循先前工作中廣泛使用的基于粒子的模擬方法，將軟體物體表示為一個粒子系統，其狀態包括粒子的位置、速度以及應變和應力信息。具體來說，粒子狀態被編碼為大小為的矩陣，其中是粒子的數量。矩陣中的每一行都包含來自單個粒子的信息：兩個表示位置和速度的 3D 向量，兩個表示形變梯度和仿射速度場的 3D 矩陣，所有信息堆疊并壓平為一個維向量。

作為運動學剛體，操縱器的末端執行器由 7D 向量表示，由 3D 位置和 4D 四元數方向組成，盡管在某些場景中可能會禁用某些自由度。對于每個任務，該表征會產生一個矩陣來編碼操縱器的完整狀態，其中為任務中所需的操縱器數量，為3或7，取決于操縱器是否需要旋轉。關于軟體和操縱器之間的交互，我們實現了剛體和軟體之間的單向耦合，并固定了所有其他物理參數，例如粒子質量和操縱器摩擦力。

觀察

雖然粒子狀態完全表征了軟體動力學，但其高自由度對于任何直接使用的規劃和控制算法都難以處理。因此，我們下采樣個粒子作為標識，并將它們的位置和速度（每個標識為 6D）疊加到大小為的矩陣中，用作粒子系統的觀察。值得注意的是，同一任務中的標識在橡皮泥的初始配置中具有固定的相對位置，從而在任務的不同配置中實現一致的粒子觀察。結合粒子觀察和操縱器狀態，我們最終得到的觀察向量具有個元素。

動作

在每個時間步長，智能體以運動學的方式更新操縱器的線速度（必要時也包括角速度），得到大小為的動作，其中為3或6，取決于操縱器是否能否旋轉。對于每個任務，我們提供全局，動作的下限和上限以穩定物理模擬。

目標和獎勵

每個任務都具備一個由質量張量表示的目標形狀，它本質上是將其密度場離散為大小為的規則網格。在每個時間步長t，我們計算當前軟體的質量張量。將目標和當前形狀離散為網格表示，便于我們通過比較相同位置的密度來定義它們的相似性，避免匹配粒子系統或點云的挑戰性問題。獎勵函數的完整定義包括一個相似性度量以及兩個關于操縱器高層次運動的正則化器：

其中，為兩個形狀的質量張量之間的距離，為兩個形狀質量張量的帶符號距離場的點積，鼓勵操縱器靠近軟體。對于所有任務，正權重都是常數。偏差確保每個環境最初的獎勵為非負值。

評估組件

PlasticineLab 共包含 10 種不同的任務（圖 2）。我們在這里描述了 4 個具有代表性的任務，其余 6 個任務在附錄 B 中有詳細說明。

這些任務及其不同配置下的變體形成了一套評估組件，用于對軟體操作算法的性能進行基準測試。每個任務有 5 種變體（總共 50 種配置），通過擾動初始和目標形狀以及操縱器的初始位置生成。

圖 2 PlasticineLab 的任務和參考解決方案，其中某些任務需要多階段規劃。

Rope 智能體需要通過兩個球形操縱器將一根長繩狀橡皮泥纏繞在一根剛性柱子上。支柱的位置在不同的配置中有所不同。

Writer 智能體需要操縱一支「筆」（通過一個垂直膠囊表示），在立方橡皮泥上繪制目標涂鴉。對于每種配置，我們通過在橡皮泥表面上繪制隨機 2D 線條來生成涂鴉。筆尖通過三維動作進行控制。

Chopsticks 智能體需要使用一雙筷子（通過兩個平行膠囊表示），拿起地上的長繩狀橡皮泥并將其旋轉到目標位置。操縱器具有 7 個自由度：6 個自由度用于移動和旋轉筷子，1 個自由度用于控制每根筷子之間的距離。

RollingPin 智能體需要學習用剛性搟面杖壓平「比薩面團」（通過立方橡皮泥表示）。我們通過具有 3 個自由度的膠囊模擬搟面杖：1）搟面杖可以垂直下降以按壓面團；2）搟面杖可沿垂直軸旋轉以改變其方向；3）智能體也可以將搟面杖在橡皮泥上滾動以將其壓平。

可微彈塑性模擬

該模擬器通過 Taichi 實現并在 CUDA 上運行。連續介質力學通過移動最小二乘材料點法進行離散化，這是一種計算機圖形學中相比 B 樣條材料點法更簡單、更有效的變體。模擬器中同時使用了拉格朗日粒子和歐拉背景網格。材料的屬性包括位置、速度、質量、密度和形變梯度。這些屬性存儲在與材料一起移動的拉格朗日粒子上，而粒子與剛體的相互作用和碰撞在背景歐拉網格上處理。

在這里我們專注于材料模型的（可微分）可塑性擴展，作為橡皮泥的一個定義特征，利用 Taichi 的反向模式自動微分系統進行大多數梯度評估。

von Mises 屈服準則

遵循 Gao 等人的工作，我們使用簡單的 von Mises 屈服準則來模擬塑性。根據 von Mises 屈服準則，橡皮泥粒子在其偏應力第二個不變量超過某個閾值時屈服（即塑性變形），并且由于材料「忘記「了其靜止狀態，因此需要對形變梯度進行投影。此過程在 MPM 文獻中通常稱為返回映射。

返回映射及其梯度

遵循 Klar 等人和 Gao 等人的工作，我們將返回映射實現為每個粒子形變梯度奇異值的 3D 投影過程。這意味著我們需要對粒子的形變梯度進行奇異值分解（SVD）過程，研究者在附錄 A 中提供了該過程的偽代碼。對于反向傳播，需要評估 SVD 的梯度。Taichi 內部的 SVD 算法具有迭代性，當用蠻力的方式自動微分時，它的數值并不穩定。我們使用 Townsend 等人提出的方法來區分 SVD。對于奇異值不明顯時分母為零的問題，遵循 Jiang 等人的方法促使分母的絕對值大于。

可微接觸模型及其軟體版本

遵循標準的 MPM 實現，使用庫侖摩擦基于網格的接觸處理來解決軟體與地板和剛體障礙物 / 操縱者的碰撞。剛體表示為隨時間變化的 SDFs。在經典的 MPM 中，接觸處理會導致沿剛軟邊界的速度發生劇烈的非平滑變化。為了提高獎勵平滑度和梯度質量，我們在反向傳播過程中使用了軟化接觸模型。對于任何網格點，模擬器計算其到剛體的有符號距離。然后我們計算一個平滑碰撞強度因子，當逐步衰減到 0 時，該因子呈指數增加。直觀來說，當剛體靠近網格點時，碰撞效果會變得更強。正參數決定了軟化接觸模型的銳度。我們使用因子線性混合碰撞投影前后的網格點速度，帶來邊界周圍的平滑過渡區以及更好的接觸梯度。

實驗

評估指標

首先為每個任務生成 5 個配置，從而生成 50 個不同的強化學習配置。我們計算歸一化增量 IoU 分數來衡量狀態是否達到目標，并使用軟 IoU 來評估當前狀態和目標之間的距離。首先提取網格質量張量，即所有網格的質量。每個非負值表示存儲于網格點中的材料數量。令兩個狀態的 3D 質量張量分別為和。我們首先將每個張量除以它們的最大幅度以將其值歸一化為：

然后，兩種狀態的軟化 IoU 通過

進行計算。歸一化增量 IoU 分數用于衡量在結束時 IoU 比初始狀態時增加了多少。對于初始狀態，結束時最后狀態以及目標狀態，歸一化增量 IoU 分數定義為。對于每項任務，我們在 5 種配置上評估算法并計算代數平均分數。

評估強化學習

隨后是在本文提出的任務上評估現有強化學習算法的性能。我們使用三種 SOTA 無模型強化學習算法：Soft Actor-Critic（SAC），Twin Delayed DDPG（TD3）和 Policy Proximal Optimization（PPO）。在每個配置上訓練每個算法 10000 輪，每輪包含 50 個環境步驟。

圖 3 展示了在每個場景上各種強化學習算法的歸一化增量 IoU 分數。大多數強化學習算法可以在 Move 任務上學習到合理的策略。然而強化學習算法很難準確匹配目標形狀，這會導致最終形狀匹配中的一個小缺陷。我們注意到智能體在探索過程中經常釋放物體，使得橡皮泥在重力作用下自由落體。然后智能體重新抓取橡皮泥變得具有挑戰性，導致訓練不穩定和令人不滿意的結果。在 Rope 任務中，智能體可以將繩子推向柱子并獲得部分獎勵，但最終無法將繩子成功繞在柱子上。TripleMove 任務增加了操縱器和立體橡皮泥的數量，對強化學習算法帶來了更大的困難，揭示了算法在擴展到高維任務方面的不足。在 Torus 任務中，算法性能似乎取決于初始策略。它們有時可以找到一個合適的方向按壓操縱器，但有時因為操縱器從不接觸橡皮泥而失敗，從而導致顯著的最終得分差異。PPO 的性能優于其他兩個，在 RollingPin 任務中，SAC 和 PPO 智能體都能找到來回壓平面團的策略，但 PPO 生成了更準確的形狀，從而具有更高的歸一化增量 IoU 分數。我們猜測此處的環境更傾向于 PPO 算法，而不依賴于 MLP 評價網絡。這可能是因為 PPO 受益于 on-policy 樣本，而 MPL 評價網絡可能無法很好地捕捉詳細的形狀變化。

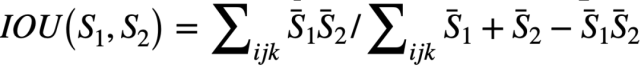
圖 3 強化學習方法在 104 個 epoch 內獲得的最終歸一化增量 IoU 分數，低于 0 的分數被限制。橙色虛線表示理論上限。

在一些更難的任務中，例如需要智能體仔細處理 3D 旋轉的 Chopsticks 任務，以及需要智能體規劃復雜軌跡以繪制痕跡的 Writer 任務，被測試的算法很少能夠在有限的時間內找到合理的解決方案。在 Assembly 任務中，所有智能體很容易陷入局部最小值。它們通常將球形橡皮泥移動到目的地附近，但未能將其抬起以得到理想的 IoU。我們期望精心設計的獎勵塑造，更好的網絡架構和細粒度的參數調整可能對環境有益。總而言之，可塑性以及軟體的高自由度對強化學習算法提出了新的挑戰。

評估軌跡優化

由于 PlasticineLab 內置可微物理引擎，我們可以使用基于梯度的優化為任務規劃開環動作序列。在基于梯度的優化中，對于從狀態開始的某個配置，初始化一個隨機動作序列。模擬器將模擬整個軌跡，在每個時間步長累積獎勵，并進行反向傳播以計算所有動作的梯度。然后我們使用基于梯度的優化方法來最大化獎勵總和。假設環境的所有信息已知。這種方法的目標不是找到可以在現實世界中執行的控制器。相反，我們希望可微物理可以有助于有效找到解決方案，并為其他控制或強化 / 模仿學習算法鋪墊基礎。

在圖 4 中，我們通過繪制獎勵曲線來證明可微物理的優化效率，并比較不同梯度下降變體的性能。我們測試 Adam 優化器（Adam）和帶動量梯度下降（GD），使用軟接觸模型來計算梯度，將 Adam 優化器與硬接觸模型（Adam-H）進行比較。對于每個優化器，我們適度為每個任務選擇 0.1 或 0.01 的學習率來處理不同任務的不同獎勵程度。值得注意的是，此處僅使用軟接觸模型來計算梯度并搜索解決方案。

我們在硬接觸環境中評估所有解決方案。在圖 4 中，額外繪制了強化學習算法的訓練曲線，以證明基于梯度的優化的效率。結果表明，基于優化的方法可以在數十次迭代內找到具有挑戰性任務的解決方案。Adam 在大多數任務中都優于 GD。這可能歸因于 Adam 的自適應學習率縮放特性，它更適合高維物理過程的復雜損失面。在大多數任務中，硬接觸模型（Adam-H）的表現不如軟模型（Adam），這驗證了軟模型通常更容易優化的直覺。

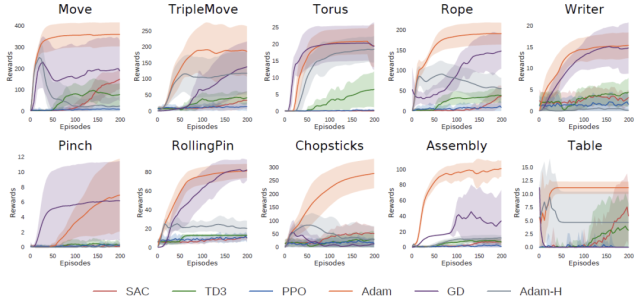
圖 4 在每個任務中獎勵及其方差隨訓練 episode 數量的變化。將獎勵限制為大于 0 以便更好的說明。

表 1 列出了所有方法的歸一化增量 IoU 分數以及標準方差。模型的全部知識為可微物理提供了獲得更有價值結果的機會。用 Adam 梯度下降可以在 Rope 任務中找到移動繩子并繞上柱子的方法，在 Assembly 任務中跳過次優解，將球體放在盒子上方，并且在 Chopsticks 任務中能夠用筷子夾起繩子。即使對于 Move 任務也能夠更好地與目標形狀對齊和更穩定的優化過程，獲得更好的性能。

對于基于梯度的方法，某些任務仍然具有挑戰性。在 TripleMove 任務中，優化器將粒子與最近目標形狀的距離最小化，這通常會導致兩個或三個橡皮泥聚集到同一個目標位置。對于沒有探索能力的基于梯度的方法來說，跳出這種局部最小值并不容易。優化器在需要多階段策略的任務上也會失敗，例如 Pinch 和 Writer 任務。在 Pinch 任務中操縱器需要按下物體，松開它們，然后再次按下。然而在操縱器和橡皮泥第一次接觸后，球形操縱器任何局部擾動都不會立即增加獎勵，優化器最終停滯。我們還注意到基于梯度的方法對初始化非常敏感。實驗將動作序列初始化為 0 左右，這在大多數環境中都具有良好的性能。

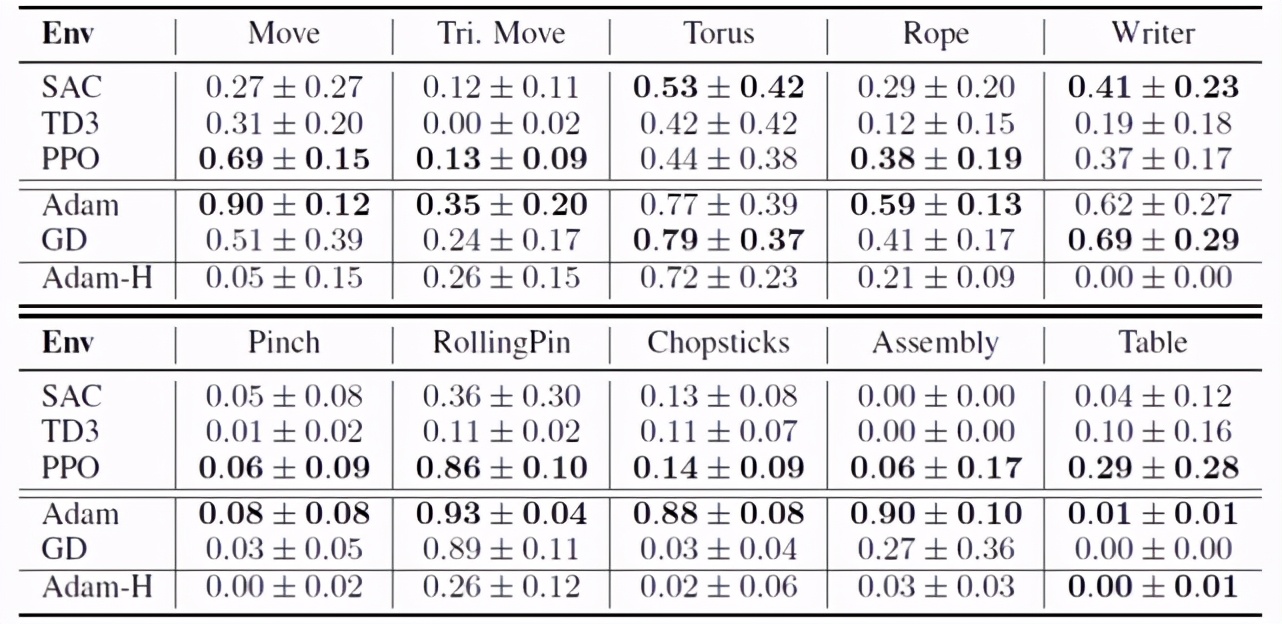
表 1 每種方法的平均歸一化增量 IoU 分數和標準方差。Adam-H 表示使用 Adam 優化器對硬接觸模型進行優化。基于強化學習的方法使用 10000 個 episode 進行訓練，基于梯度的方法使用 200 個 episode 進行優化。

潛在研究問題

該環境為基于學習的軟體操作提供了豐富的研究機遇。實驗表明，微分物理學能夠使基于梯度的軌跡優化算法以極快的速度解決簡單的規劃任務，因為梯度為改進策略提供了強大而清晰的指導。但是，如果任務涉及操縱器和橡皮泥之間的分離和重新連接，則梯度會消失。當無法使用基于局部擾動分析的基于梯度的優化時，我們可能會考慮那些允許多步探索并累積獎勵的方法，例如隨機搜索和強化學習。

因此，如何將可微物理與基于采樣的方法相結合來解決軟體操作規劃問題，會非常有趣。除了規劃問題之外，研究如何在這種環境中設計和學習有效的軟體操縱控制器也非常有趣。實驗結果表明控制器設計和優化仍有足夠的改進空間，可能的方向包括為強化學習設計更好的獎勵函數和研究合適的 3D 深度神經網絡結構以捕獲軟體動力學。

第三個有趣的方向是將 PlasticineLab 中訓練有素的策略轉移到現實世界中。雖然這個問題在很大程度上未被探索，但我們相信我們的模擬器可以在各種方面提供幫助：

1. 如 Gaume 等人所示，MPM 仿真結果可以準確匹配現實世界。在未來的工作中，我們可能會使用模擬器為復雜任務規劃一個高級軌跡，然后結合低級控制器來執行規劃；

2. 該微分模擬器可以計算物理參數的梯度并優化參數以擬合數據，這可能有助于縮小 sim2real 差距；

3.PlasticineLab 還可以結合域隨機化和其他 sim2real 方法。可以在該模擬器中自定義物理參數和圖像渲染器以實現域隨機化。我們希望該模擬器可以作為一個很好的工具來研究現實世界的軟體操作問題。

最后，泛化性是一個重要的探索方向。該研究的平臺支持過程生成，可以生成和模擬不同物體的各種配置，評估不同算法的通用性。PlasticineLab 也為設計豐富的目標條件任務提供了良好的平臺。