寫給小白看的遞歸(硬核)
大家好,我是bigsai,之前有老弟說弄不懂遞歸,今天給大家講講遞歸。
什么是遞歸?
遞歸:就是函數自己調用自己。子問題須與原始問題為同樣的事,或者更為簡單。
遞歸通常可以簡單的處理子問題,但是不一定是最好的解決方式。
對于遞歸要分清以下概念:
- 遞歸是自己調用自己
- 遞歸通常不在意具體操作,只關心初始條件、結束條件和上下層的變化關系。
- 遞歸函數需要有臨界停止點(結束條件),即遞歸不能無限制的執行下去。通常這個點為必須經過的一個數。
- 遞歸可以被棧替代。有些遞歸可以優化。比如遇到重復性的可以借助空間內存記錄而減少遞歸的次數
認識遞歸,遞歸函數通常看起來簡易但是對于初學者可能很難去理解它,拿一個遞歸函數來說。
- static void digui()
- {
- System.out.println("bigsai前");
- digui();
- System.out.println("bigsai后");
- }
這是一個遞歸嘛?不是正常遞歸,沒有結束條件,自己一致調用自己導致無限循環。
那正確的遞歸應該這樣
- static void digui(int time)
- {
- if(time==0) {}//time==0不執行
- else {
- System.out.println("bigsai前time: "+time);
- digui(time-1);
- System.out.println("bigsai后time: "+time);
- }
- }
對于這樣一種遞歸,它的流程大致是這樣的
- 定義遞歸算法及參數
- - 停止遞歸算法條件
- - (可存在)其他邏輯
- - 遞歸調用(參數需要改變)
- - (可存在)其他邏輯
所以,調用digui(5)在控制臺輸出是這樣的
那么,我想你對遞歸函數執行的流程應該有所了解了吧。
遞歸求階乘
初學遞歸,接觸最多的就是遞歸求階乘,為啥階乘可以用遞歸來求呢? 我們首先看下階乘,n的階乘表示為:
n!=n*(n-1)*……*1
n的階乘就是從1開始疊乘到n,那么n-1的階乘為:
(n-1)!=(n-1)*(n-2)*……*1
通過觀察就能知道n的階乘和n-1的階乘有這樣的關系:
n!=n!=n*(n-1)!
所以,我們要求n的階乘,我們知道n-1的階乘乘以n就可以得到,這就是最核心的關系。
0的階乘為1,通過階乘上下級的關系,我們假設一個函數jiecheng(n)為求n的階乘的函數,那么這個函數為:
- static int jiecheng(int n)
- {
- if(n==0)//0的階乘為1
- {
- return 1;
- }
- else {
- return n*jiecheng(n-1);//return n*(n-1)*jiecheng(n-2)=-------
- }
- }
運行流程為這樣:
遞歸求斐波那契
斐波那契數列,已經跟隨我們成長很久很久了,除了直接的斐波那契,爬樓梯等問題也和斐波那契問題差不多。
首先,求斐波那契的公式為:
F[n]=F[n-1]+F[n-2](n>=3,F[1]=1,F[2]=1)
也就是除了n=1和2特殊以外,其他均是可以使用遞推式,按照上述遞歸思想,我們假設求斐波那契設成F(n);
那么遞推實現的代碼為:
- static long F(int n)
- {
- if(n==1||n==2) {return 1;}
- else {
- return F(n-1)+F(n-2);
- }
- }
其實它的調用流程為:
不過這個斐波那契這樣的求法效率并不高,后面會提一嘴。
遞歸解決漢諾塔
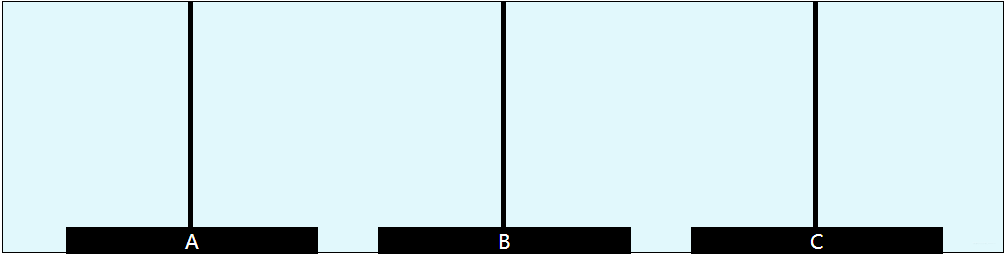
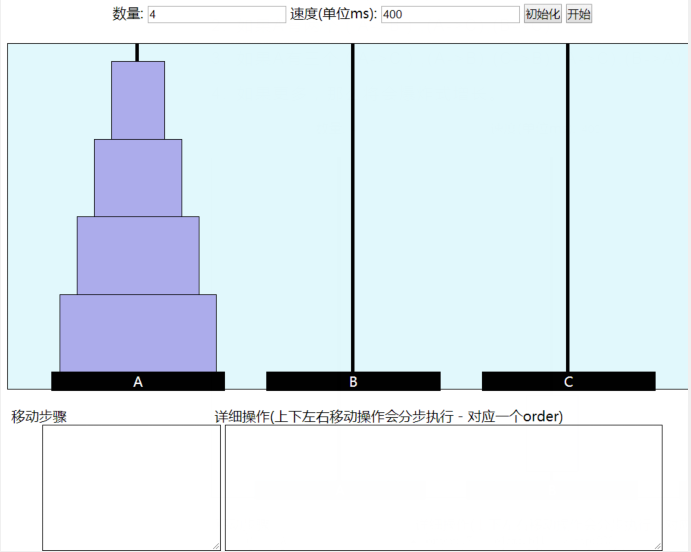
漢諾塔是經典遞歸問題:
- 相傳在古印度圣廟中,有一種被稱為漢諾塔(Hanoi)的游戲。該游戲是在一塊銅板裝置上,有三根桿(編號A、B、C),在A桿自下而上、由大到小按順序放置64個金盤(如下圖)。游戲的目標:把A桿上的金盤全部移到C桿上,并仍保持原有順序疊好。操作規則:每次只能移動一個盤子,并且在移動過程中三根桿上都始終保持大盤在下,小盤在上,操作過程中盤子可以置于A、B、C任一桿上。
- 如果A只有一個(A->C)
- 如果A有兩個(A->B),(A->C),(B->C)
- 如果A有三個(A->C),(A->B),(C->B),(A->C),(B->A),(B->C),(A->C).
- 如果更多,那么將會爆炸式增長。
可以發現每增加一步,其中的步驟會多很多,如果一步步想,很難想明白,所以要用遞歸全局的想法看問題。
當有1個要從A->C時,這里使用函數move(A,C)表示(其他move操作同理)。
用hannuo(n)函數表示總共n個盤子要從A->C。
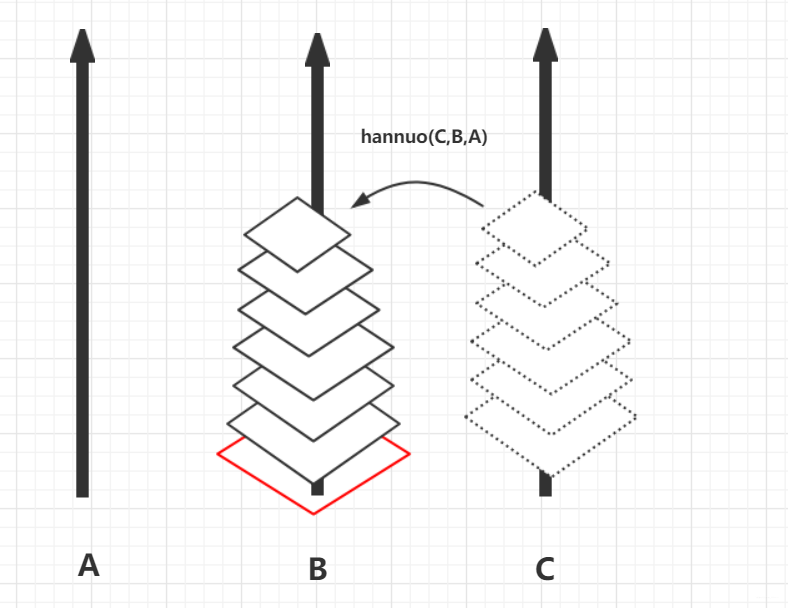
遞歸,其實就是要找上下層的關系,n個盤子從A挪到C和n-1個盤子從A挪到C有啥聯系(hannuo(n)—>hannuo(n-1)有啥關系)。下面帶你一步步分析。
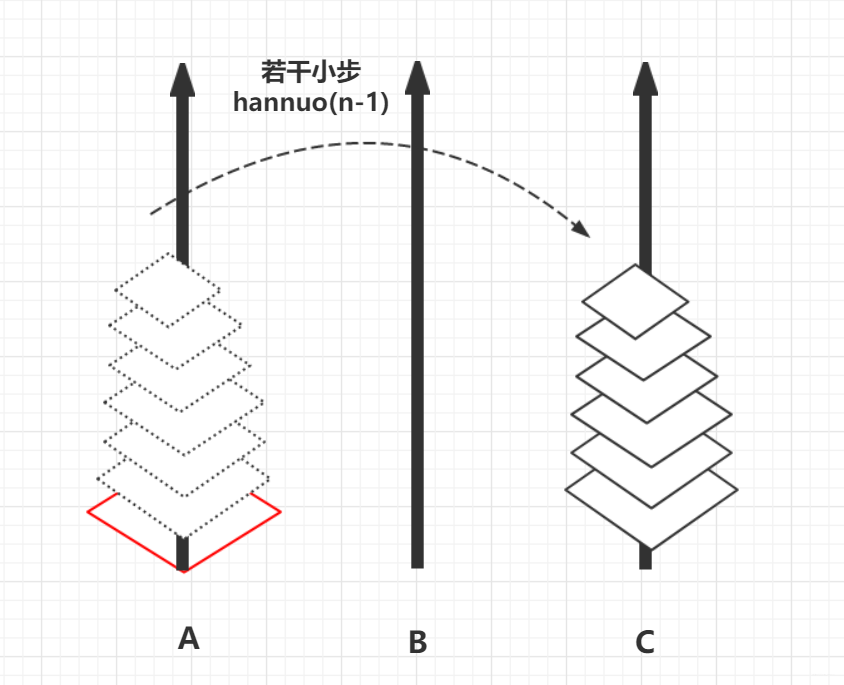
假設有n個盤子
hannuo(n-1)之后n-1個盤子從A—>C.
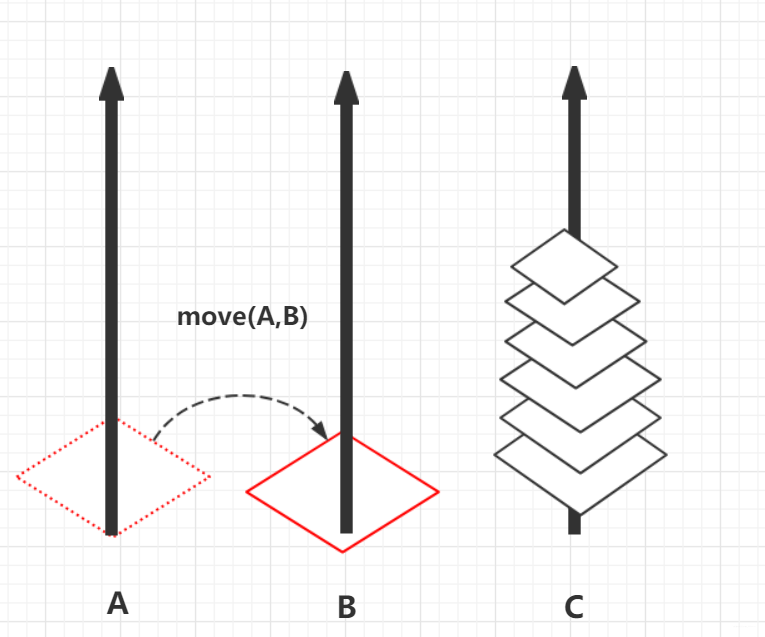
此時剩下底下最大的,只能移動到B,move(A,B)
那么你是否發現什么眉目了,只需原先的huannuo(n-1)相同操作從C—>B即可完成轉移到B,所以這個需要加參數表示其方向性,那么我們的之前函數應該寫成hannuo(n-1,A,C),但是這里肯定又用到B(向下需要用到),所以把B傳進來hannuo(n-1,A,B,C)先表示為從n-1個從A(借助B執行若干操作)轉到C。
這一系列操作使得將n個盤子從A—>B但是我們要的是A—>C才是需要的hannuo(n,A,B,C),這個很容易啊我們只需要第一步將n-1挪到B上就可以了啊。
經過上面分析,那么完整的操作為:
- package 遞歸;
- public class hannuota {
- static void move(char a,char b)
- {
- System.out.println("移動最上層的"+ a+ "到"+ b+ "\t");
- }
- static void hannuota(int n,char a,char b,char c)//主要分析每一大步對于下一步需要走的。
- {
- if(n==1) {move(a,c);}//從a移到c
- else
- {
- hannuota(n-1,a,c,b);//將n-1個從a借助c移到b
- move(a,c); //將第n(最后一個)從a移到c。
- hannuota(n-1,b,a,c);//再將n-1個從b借助a移到c
- }
- }
- public static void main(String[] args)
- {
- hannuota(5,'a','b','c');
- }
- }
這樣,漢諾塔問題是不是搞懂了?
遞歸 VS 記憶化
很多時候,遞歸的效率是很低的(一個遞歸拆分成兩個及以上子問題效率就不太行了),我們要用動態規劃或者記憶化去優化,為什么要記憶化?因為遞歸成子問題,子問題再拆分成子問題,造成很多的重復計算!
比如上面說到的遞歸求斐波那契數列,就是一個效率非常低的算法,比如你看看F(5)是這樣走的:
在遞歸求F(4)時候,F(4)遞歸會求解F(3),但是右側的還會再執行一遍。如果是數量非常大的數,那么將耗費很大的時間。所以我們就可以采取記憶化!第一次算出結果的時候就存儲一下,如果是線性有規律(大部分)就用數組,否則就用HashMap存儲。
具體實現的代碼為:
- static long F(int n,long record[])
- {
- if(n==1||n==2) {return 1;}
- if(record[n]>0)
- return record[n];
- else
- record[n]=F(n-1,record)+F(n-2,record);
- return record[n];
- }
- public static void main(String[] args) {
- int n=6;
- long[] record = new long[n+1];
- System.out.println(F(n,record));
- }
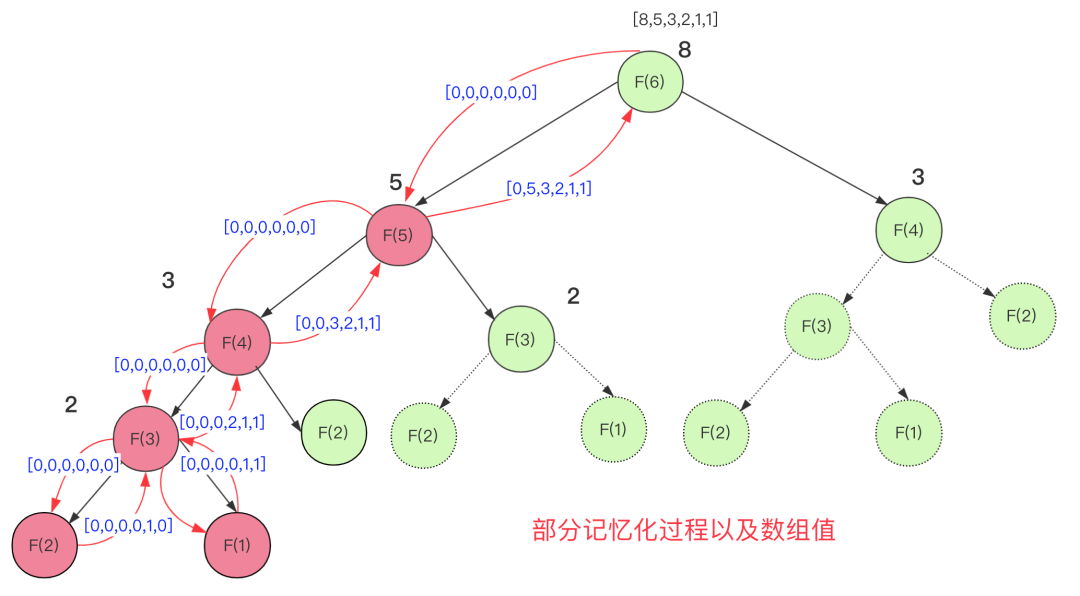
這樣可以節省很多時間,尤其是n非常大的情況(遞歸是指數級別增長,記憶化是線性級別)。例如一個F(6)求解過程:
當然,記憶化的問題遠遠不止這么多,具體還需要自行學習。
遞歸 VS 數據結構
遞歸在很多場景都有很好的應用,在鏈表中、二叉樹、圖中(搜索算法)都有很多的應用,這里就舉一些非常經典的例子。
比如在鏈表中,很經典的就是鏈表逆序輸出、鏈表反轉問題,比如鏈表反轉問題,對應力扣206(給你單鏈表的頭節點 head ,請你反轉鏈表,并返回反轉后的鏈表),可以這樣巧妙的實現:
- /**
- * Definition for singly-linked list.
- * public class ListNode {
- * int val;
- * ListNode next;
- * ListNode() {}
- * ListNode(int val) { this.val = val; }
- * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
- * }
- */
- class Solution {
- public ListNode reverseList(ListNode head) {
- if(head==null||head.next==null)
- return head;
- ListNode node =reverseList(head.next);//返回最后的鏈表節點
- head.next.next=head;//后一個節點指向自己
- head.next=null;//自己next指向null
- return node;
- }
- }
對于二叉樹,最經典的就是二叉樹的前序、中序、后序遍歷的遞歸實現方式:
例如二叉樹前序遍歷:
- public void qianxu(node t)// 前序遞歸 前序遍歷:根結點 ---> 左子樹 ---> 右子樹
- {
- if (t != null) {
- System.out.print(t.value + " ");// 當前節點
- qianxu(t.left);
- qianxu(t.right);
- }
- }
二叉樹中序遍歷:
- public void zhongxu(node t)// 中序遍歷 中序遍歷:左子樹---> 根結點 ---> 右子樹
- {
- if (t != null) {
- zhongxu(t.left);
- System.out.print(t.value + " ");// 訪問完左節點訪問當前節點
- zhongxu(t.right);
- }
- }
二叉樹的后序遍歷:
- public void houxu(node t)// 后序遍歷 后序遍歷:左子樹 ---> 右子樹 ---> 根結點
- {
- if (t != null) {
- houxu(t.left);
- houxu(t.right);
- System.out.print(t.value + " "); // 訪問玩左右訪問當前節點
- }
- }
遞歸 VS 常見算法在我們熟知很多算法都與遞歸有著很大關系。比如dfs深度優先遍歷、回溯算法、分治算法等,這里只是簡單介紹一下。
遞歸只是計算機執行一種方式,一個來回的過程,所以這個過程可以被一些算法很巧妙的運用。
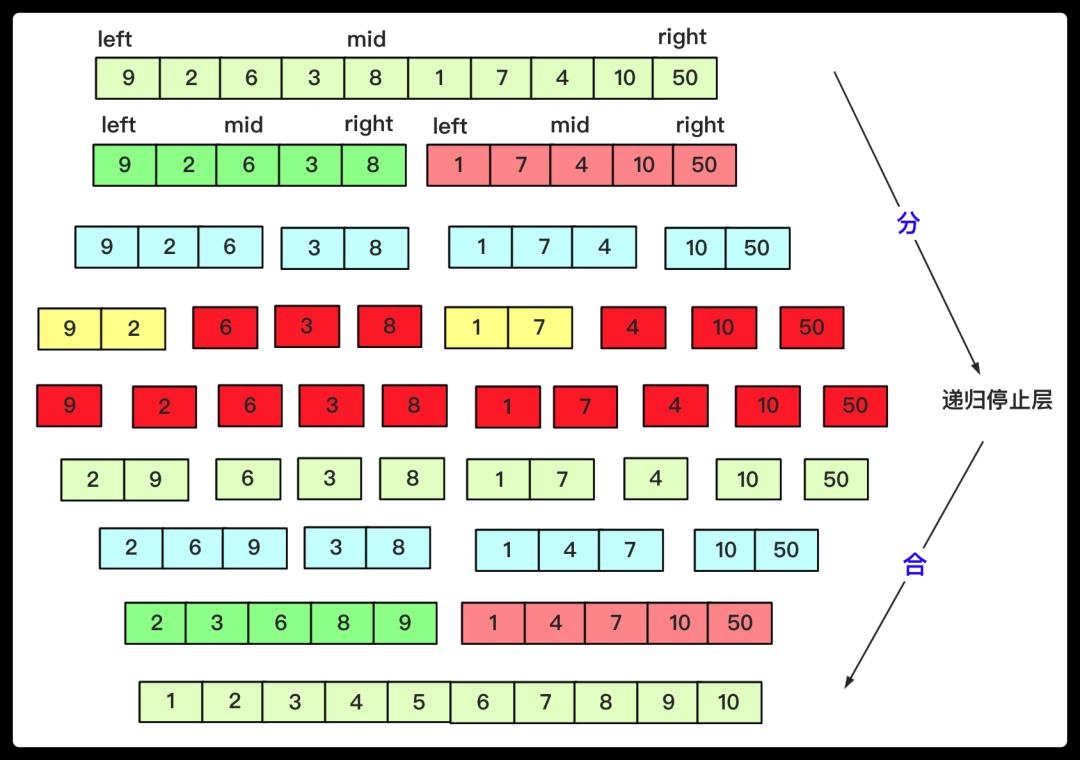
分治算法:將問題分解成多個子問題,子問題求解完合并得到結果,這個過程可以使用遞歸實現(也可能不使用遞歸),但大部分會用遞歸因為實現更加簡潔,它和斐波那契遞歸不同的是它分裂的子問題一般沒有重復的(即分完為止而不會重復計算)。常見的快排、歸并排序都是使用分治算法,其算法實現借助遞歸。例如歸并排序其流程:
算法實現為:
- private static void mergesort(int[] array, int left, int right) {
- int mid=(left+right)/2;
- if(left<right)
- {
- mergesort(array, left, mid);
- mergesort(array, mid+1, right);
- merge(array, left,mid, right);
- }
- }
- private static void merge(int[] array, int l, int mid, int r) {
- int lindex=l;int rindex=mid+1;
- int team[]=new int[r-l+1];
- int teamindex=0;
- while (lindex<=mid&&rindex<=r) {//先左右比較合并
- if(array[lindex]<=array[rindex])
- {
- team[teamindex++]=array[lindex++];
- }
- else {
- team[teamindex++]=array[rindex++];
- }
- }
- while(lindex<=mid)//當一個越界后剩余按序列添加即可
- {
- team[teamindex++]=array[lindex++];
- }
- while(rindex<=r)
- {
- team[teamindex++]=array[rindex++];
- }
- for(int i=0;i<teamindex;i++)
- {
- array[l+i]=team[i];
- }
- }
dfs、回溯法 通常想著枚舉盡可能多的情況,很多時候我們并不能很好知道運行界限是在哪,并且運行中狀態可能會有所變化,所以我們可以寫好限定條件使用遞歸去實現,遞歸的歸過程也可很好的復原去進行其他試探。包括二叉樹的前中后遍歷都蘊涵dfs算法思想,而回溯算法則是經典全排列、八皇后問題代表。
其流程通常為:
- 定義回溯算法及參數
- - (符合條件)跳出
- - (不符合)不跳出:
- - - 遍歷需要操作的列表&&該元素可操作&&可以繼續試探
- - - - 標記該元素已使用以及其他操作
- - - - 遞歸調用(參數改變)
- - - - 清除該元素標記以及其他操作
此外,遞歸還在很多算法中有廣泛的應用,這里就不具體列舉啦!
結語
今天遞歸就講到這里啦,學好遞歸沒那么容易,還是要具體掌握各種算法、題目才能慢慢領略遞歸精髓,遞歸用好可以寫出很多騷代碼!
不過實際題目注重效率和便捷,不能盲目追求效率,也不能盲目使用遞歸不注意算法優化。