[[413220]]

二值化網(wǎng)絡(luò)（BNN）是一種網(wǎng)絡(luò)壓縮方法，把原本需要 32 bit 表示的神經(jīng)網(wǎng)絡(luò)參數(shù)值和激活值都二值化到只需要用 1 bit 表示，即 -1/+1 表示。

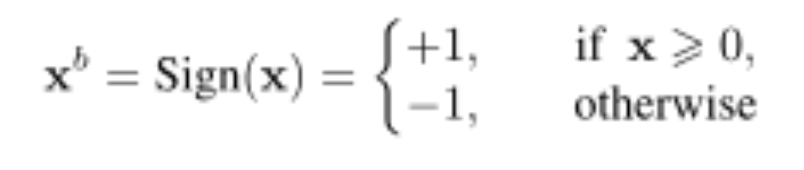
這種極度的壓縮方法在帶來優(yōu)越的壓縮性能的同時，會造成網(wǎng)絡(luò)精度的下降。

在今年的 ICML 會議中，一篇來自 CMU 和 HKUST 科研團隊的論文僅通過調(diào)整訓(xùn)練算法，在 ImageNet 數(shù)據(jù)集上取得了比之前的 SOTA BNN 網(wǎng)絡(luò) ReActNet 高 1.1% 的分類精度，最終的 top-1 accuracy 達到 70.5%，超過了所有同等量級的二值化網(wǎng)絡(luò)，如下圖所示。

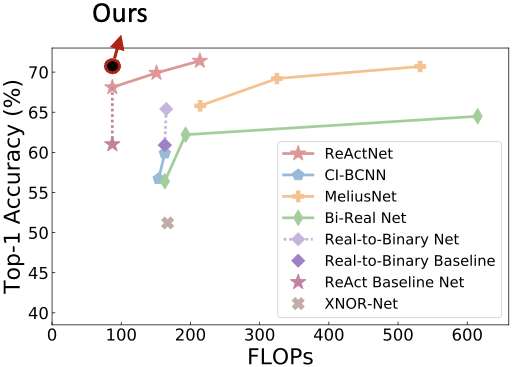
這篇論文從二值化網(wǎng)絡(luò)訓(xùn)練過程中的常見問題切入，一步步給出對應(yīng)的解決方案，最后收斂到了一個實用化的訓(xùn)練策略。接下來就跟著這篇論文一起看看二值化網(wǎng)絡(luò)（BNN）應(yīng)該如何優(yōu)化。

• 論文地址：https://arxiv.org/abs/2106.11309
• 代碼地址：https://github.com/liuzechun/AdamBNN

首先，BNN 的優(yōu)化器應(yīng)該如何選取?

可以看到，BNN 的優(yōu)化曲面明顯不同于實數(shù)值網(wǎng)絡(luò)，如下圖所示。實數(shù)值網(wǎng)絡(luò)在局部最小值附近有更加平滑的曲面，因此實數(shù)值網(wǎng)絡(luò)也更容易泛化到測試集。相比而言，BNN 的優(yōu)化曲面更陡，因此泛化性差并且優(yōu)化難度大。

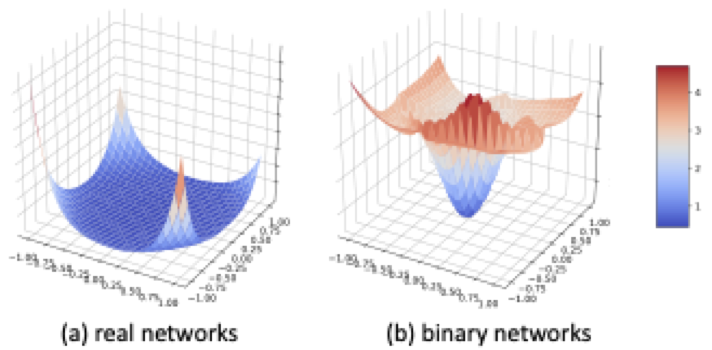
這個明顯的優(yōu)化區(qū)別也導(dǎo)致了直接沿用實數(shù)值網(wǎng)絡(luò)的 optimizer 在 BNN 上表現(xiàn)效果并不好。目前實數(shù)值分類網(wǎng)絡(luò)的通用優(yōu)化器都是 SGD，該論文的對比實驗也發(fā)現(xiàn)，對于實數(shù)值網(wǎng)絡(luò)而言，SGD 的性能總是優(yōu)于自適應(yīng)優(yōu)化器 Adam。但對于 BNN 而言，SGD 的性能卻不如 Adam，如下圖所示。這就引發(fā)了一個問題：為什么 SGD 在實數(shù)值分類網(wǎng)絡(luò)中是默認(rèn)的通用優(yōu)化器，卻在 BNN 優(yōu)化中輸給了 Adam 呢？

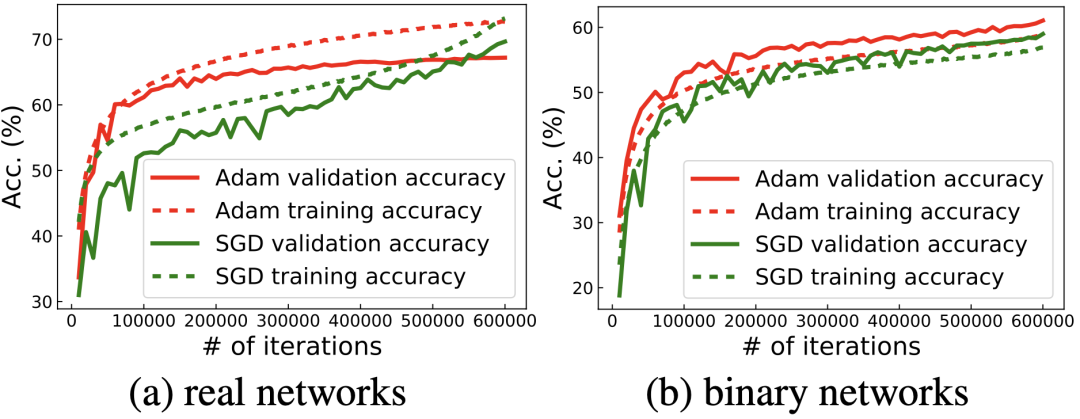
這就要從 BNN 的特性說起。因為 BNN 中的參數(shù)值（weight）和激活值（activation）都是二值化的，這就需要用 sign 函數(shù)來把實數(shù)值的參數(shù)和激活值變成二值化。

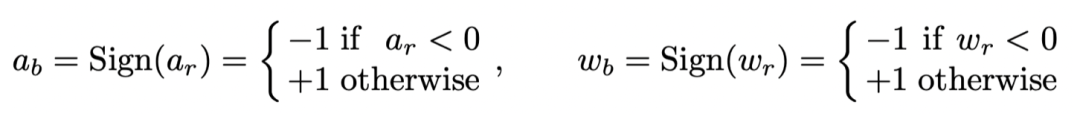
而這個 Sign 函數(shù)是不可導(dǎo)的，所以常規(guī)做法就是對于二值化的激活值用 Clip 函數(shù)的導(dǎo)數(shù)擬合 Sign 函數(shù)的導(dǎo)數(shù)。

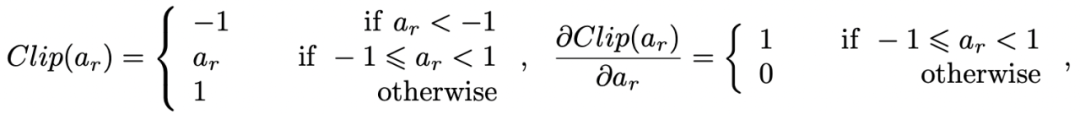
這樣做有一個問題就是，當(dāng)實數(shù)值的激活值超出了 [-1，1] 的范圍，稱為激活值過飽和（activation saturation），對應(yīng)的導(dǎo)數(shù)值就會變?yōu)?0。從而導(dǎo)致了臭名昭著的梯度消失（gradient vanishing）問題。從下圖的可視化結(jié)果中可以看出，網(wǎng)絡(luò)內(nèi)部的激活值超出[-1, 1] 范圍十分常見，所以二值化優(yōu)化里的一個重要問題就是由于激活值過飽和導(dǎo)致的梯度消失，使得參數(shù)得不到充分的梯度估計來學(xué)習(xí)，從而容易困局部次優(yōu)解里。

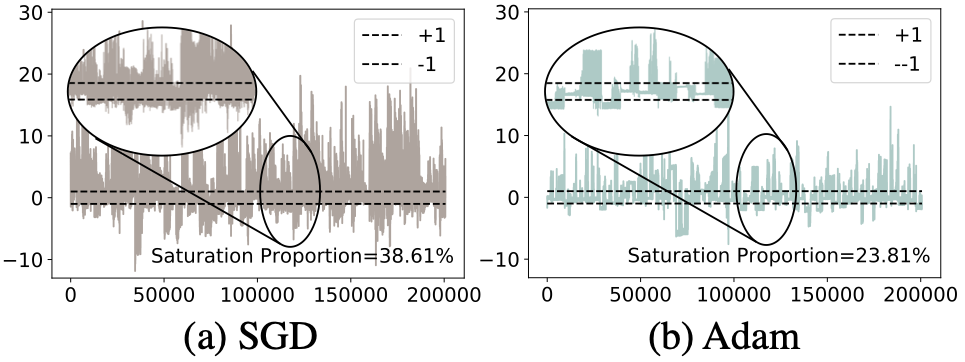
而比較 SGD 而言，Adam 優(yōu)化的二值化網(wǎng)絡(luò)中激活值過飽和問題和梯度消失問題都有所緩解。這也是 Adam 在 BNN 上效果優(yōu)于 SGD 的原因。那么為什么 Adam 就能緩解梯度消失的問題呢？這篇論文通過一個構(gòu)造的超簡二維二值網(wǎng)絡(luò)分析來分析 Adam 和 SGD 優(yōu)化過程中的軌跡：

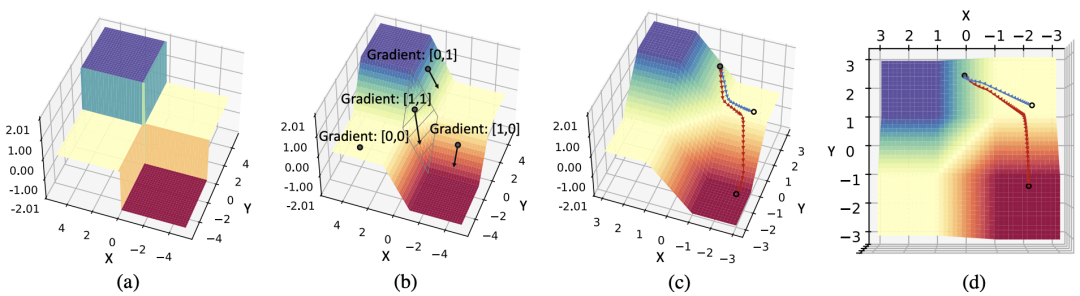
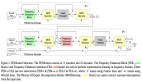
圖中展示了用兩個二元節(jié)點構(gòu)建的網(wǎng)絡(luò)的優(yōu)化曲面。(a) 前向傳遞中，由于二值化函數(shù) Sign 的存在，優(yōu)化曲面是離散的，(b) 而反向傳播中，由于用了 Clip(−1, x, 1)的導(dǎo)數(shù)近似 Sign(x)的導(dǎo)數(shù)，所以實際優(yōu)化的空間是由 Clip(−1, x, 1)函數(shù)組成的， (c) 從實際的優(yōu)化的軌跡可以看出，相比 SGD，Adam 優(yōu)化器更能克服零梯度的局部最優(yōu)解，(d) 實際優(yōu)化軌跡的頂視圖。

在圖 (b) 所示中，反向梯度計算的時候，只有當(dāng) X 和 Y 方向都落在[-1, 1] 的范圍內(nèi)的時候，才在兩個方向都有梯度，而在這個區(qū)域之外的區(qū)域，至少有一個方向梯度消失。

而從下式的 SGD 與 Adam 的優(yōu)化方式比較中可以看出，SGD 的優(yōu)化方式只計算 first moment，即梯度的平均值，遇到梯度消失問題，對相應(yīng)的參數(shù)的更新值下降極快。而在 Adam 中，Adam 會累加 second moment，即梯度的二次方的平均值，從而在梯度消失的方向，對應(yīng)放大學(xué)習(xí)率，增大梯度消失方向的參數(shù)更新值。這樣能幫助網(wǎng)絡(luò)越過局部的零梯度區(qū)域達到更好的解空間。

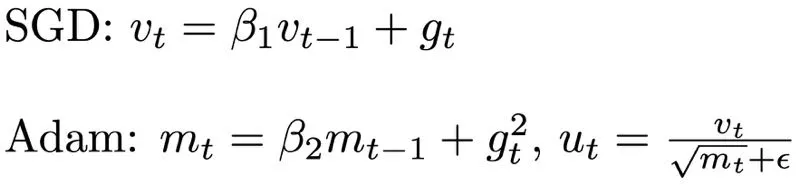
進一步，這篇論文展示了一個很有趣的現(xiàn)象，在優(yōu)化好的 BNN 中，網(wǎng)絡(luò)內(nèi)部存儲的用于幫助優(yōu)化的實數(shù)值參數(shù)呈現(xiàn)一個有規(guī)律的分布：

分布分為三個峰，分別在 0 附近，-1 附近和 1 附近。而且 Adam 優(yōu)化的 BNN 中實數(shù)值參數(shù)接近 - 1 和 1 的比較多。這個特殊的分布現(xiàn)象就要從 BNN 中實數(shù)值參數(shù)的作用和物理意義講起。BNN 中，由于二值化參數(shù)無法直接被數(shù)量級為 10^ -4 左右大小的導(dǎo)數(shù)更新，所以需要存儲實數(shù)值參數(shù)，來積累這些很小的導(dǎo)數(shù)值，然后在每次正向計算 loss 的時候取實數(shù)值參數(shù)的 Sign 作為二值化參數(shù)，這樣計算出來的 loss 和導(dǎo)數(shù)再更新實數(shù)值參數(shù)，如下圖所示。

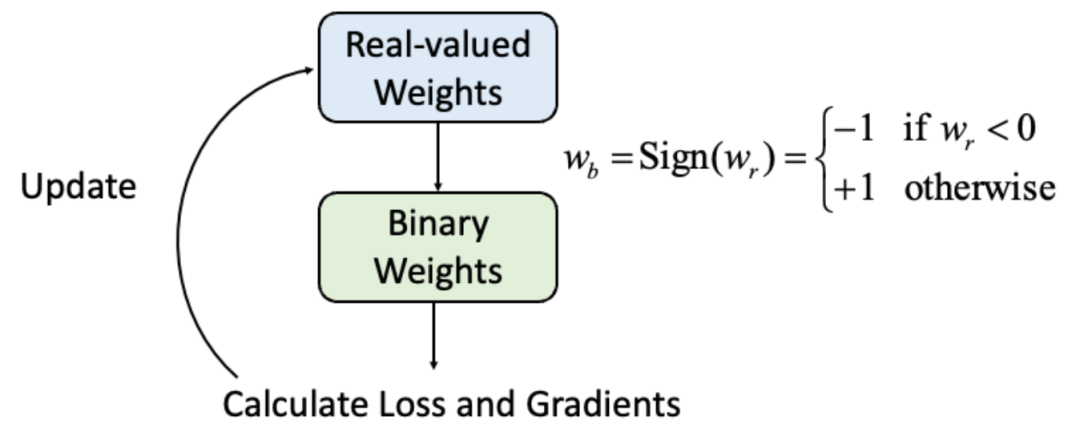
所以，當(dāng)這些實數(shù)值參數(shù)靠近零值時，它們很容易通過梯度更新就改變符號，導(dǎo)致對應(yīng)的二值化參數(shù)容易跳變。而當(dāng)實值參數(shù)的絕對值較高時，就需要累加更多往相反方向的梯度，才能使得對應(yīng)的二值參數(shù)改變符號。所以正如 (Helwegen et al., 2019) 中提到的，實值參數(shù)的絕對值的物理意義可以視作其對應(yīng)二值參數(shù)的置信度。實值參數(shù)的絕對值越大，對應(yīng)二值參數(shù)置信度更高，更不容易改變符號。從這個角度來看，Adam 學(xué)習(xí)的網(wǎng)絡(luò)比 SGD 實值網(wǎng)絡(luò)更有置信度，也側(cè)面印證了 Adam 對于 BNN 而言是更優(yōu)的 optimizer。

當(dāng)然，實值參數(shù)的絕對值代表了其對應(yīng)二值參數(shù)的置信度這個推論就引發(fā)了另一個思考：應(yīng)不應(yīng)該在 BNN 中對實值參數(shù)施加 weight decay?

在實數(shù)值網(wǎng)絡(luò)中，對參數(shù)施加 weight decay 是為了控制參數(shù)的大小，防止過擬合。而在二值化網(wǎng)絡(luò)中，參與網(wǎng)絡(luò)計算的是實數(shù)值參數(shù)的符號，所以加在實數(shù)值參數(shù)上的 weight decay 并不會影響二值化參數(shù)的大小，這也就意味著，weight decay 在二值化網(wǎng)絡(luò)中的作用也需要重新思考。

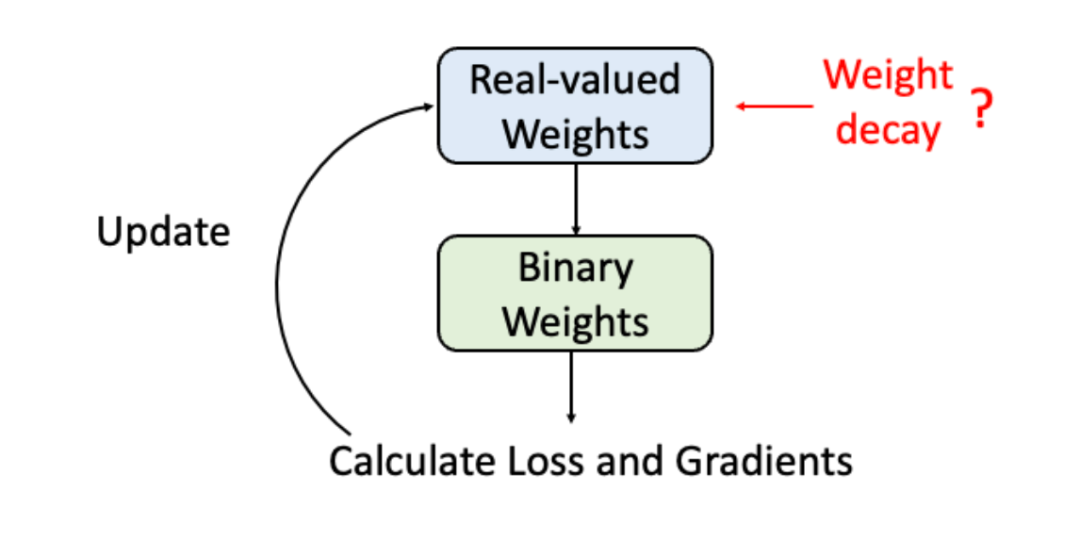
這篇論文發(fā)現(xiàn)，二值化網(wǎng)絡(luò)中使用 weight decay 會帶來一個困境：高 weight decay 會降低實值參數(shù)的大小，進而導(dǎo)致二值參數(shù)易變符號且不穩(wěn)定。而低 weight decay 或者不加 weight decay 會使得二值參數(shù)將趨向于保持當(dāng)前狀態(tài)，而導(dǎo)致網(wǎng)絡(luò)容易依賴初始值。

為了量化穩(wěn)定性和初始值依賴性，該論文引入了兩個指標(biāo)：用于衡量優(yōu)化穩(wěn)定性的參數(shù)翻轉(zhuǎn)比率（FF-ratio），以及用于衡量對初始化的依賴性的初始值相關(guān)度 (C2I-ratio)。兩者的公式如下，

FF-ratio 計算了在第 t 次迭代更新后多少參數(shù)改變了它們的符號，而 C2I -ratio 計算了多少參數(shù)與其初始值符號不同。

從下表的量化分析不同的 weight decay 對網(wǎng)絡(luò)穩(wěn)定性和初始值依賴性的結(jié)果中可以看出，隨著 weight decay 的增加，F(xiàn)F-ratio 與 C2I-ratio 的變化趨勢呈負(fù)相關(guān)，并且 FF-ratio 呈指數(shù)增加，而 C2I-ratio 呈線性下降。這表明一些參數(shù)值的來回跳變對最終參數(shù)沒有貢獻，而只會影響訓(xùn)練穩(wěn)定性。

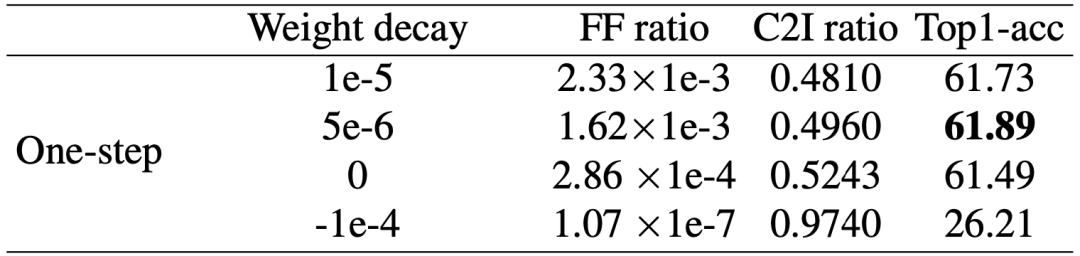
那么 weight decay 帶來的穩(wěn)定性和初始值依賴性的兩難困境有沒有方法解離呢? 該論文發(fā)現(xiàn)最近在 ReActNet (Liu et al., 2020) 和 Real-to-Binary Network (Brais Martinez, 2020) 中提出的兩階段訓(xùn)練法配合合適的 weight-decay 策略能很好地化解這個困境。這個策略是，第一階段訓(xùn)練中，只對激活值進行二值化，不二值化參數(shù)。由于實數(shù)值參數(shù)不必?fù)?dān)心二值化參數(shù)跳變的問題，可以添加 weight decay 來減小初始值依賴。隨后在第二階段訓(xùn)練中，二值化激活值和參數(shù)，同時用來自第一步訓(xùn)練好的參數(shù)初始化二值網(wǎng)絡(luò)中的實值參數(shù)，不施加 weight decay。這樣可以提高穩(wěn)定性并利用預(yù)訓(xùn)練的良好初始化減小初始值依賴帶來的弊端。通過觀察 FF-ratio 和 C2I-ratio，該論文得出結(jié)論，第一階段使用 5e-6 的 weight-decay，第二階段不施加 weight-decay 效果最優(yōu)。

該論文綜合所有分析得出的訓(xùn)練策略，在用相同的網(wǎng)絡(luò)結(jié)構(gòu)的情況下，取得了比 state-of-the-art ReActNet 超出 1.1% 的結(jié)果。實驗結(jié)果如下表所示。

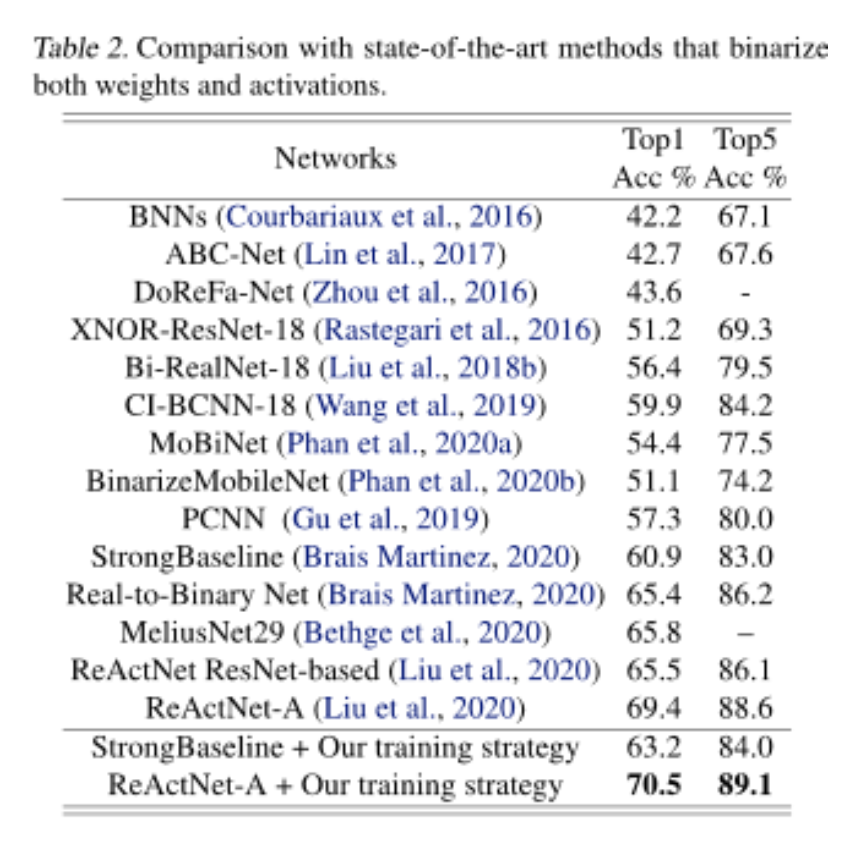
更多的分析和結(jié)果可以參考原論文。