[[416187]]

本文轉自雷鋒網，如需轉載請至雷鋒網官網申請授權。

一般情況下，當你要對某個特定地區的植物進行調查時，你可能會按植物的種類來劃分。

就這種方法來看，如果是沿著托斯卡納海岸的某些地帶做這類調查并不會很困難，因為你大概率只會發現一種植物，就是海松（pinus pinaster）。但是，如果你要在亞馬遜熱帶雨林中做植物統計，那你要找出雨林里所有植物的名字與數量就會非常困難，甚至可以說是“毫無可能”。

在探索廣闊數學圖景的征程上，數學家們也可能會遇到類似的挑戰，尤其是對研究描述集合論的數學家而言，因為他們要嘗試對分類問題的難度進行評級。有時候他們會認為某個分類任務很容易，有時候又會覺得某個分類任務太難，比如上述的亞馬遜雨林植物分類問題。

描述集合論（descriptive set theory）只是集合論的一個分支，主要研究物體的集合，可以是數字、圖形、空間中的點、向量，等等。實數、有理數、虛數本身就是一個集合。可以說，數學家的研究范圍涵蓋了方方面面。

幾十年來，研究人員一直被一個分類問題所困擾。這個分類問題就是“無撓阿貝爾群”（torsion-free abelian groups，簡稱“TFAB”）。

TFAB 問題最早由數學家 Harvey Friedman 和 Lee Stanley 在1989年所發表的一篇論文（“A Borel Reducibility Theory For Classes of Countable Structures”）中提出。在這篇論文中，Harvey Friedman 與 Lee Stanley 介紹了一種比較可數結構分類問題難度的新方法，表明有些分類問題會非常復雜。

論文地址：https://www.jstor.org/stable/2274750?seq=1

這個問題困擾了數學家們30多年。今年，都靈大學的數學家 Gianluca Paolini 與他之前的博士后導師、希伯來大學教授 Saharon Shelah 在網上發表的一篇論文（如下）終于解決了 TFAB 的相關問題。

論文地址：https://arxiv.org/pdf/2102.12371.pdf

1

計算無窮大

TFAB 問題涉及到一類無窮可數結構，可以幫我們理解數學家如何處理這些看似笨拙的數量。

首先，一組結構“可數”意味著什么？自然數 (0, 1, 2, 3 ...) 是無窮的，但也被視為“可數”，所以自然數有時候也會被稱為“可數數”（counting number）。如果你按順序數這些自然數，它們可以完整地排列，（雖然你要花無窮的時間）。自然數集合中的元素，或者它的“基數”，被標記為“aleph-zero”。數學家把任何與自然數無窮集大小相同的集合都稱為“可數”集合。

相反，實數（包括自然數、有理數和無理數）雖然也是無窮的，但它們卻被歸類為“不可數”。主要原因是實數太多：我們從19世紀80年代后期就知道，0 和 1 之間的實數比所有自然數加起來還要多。

所以有這么一種說法：無窮并非生而平等；有些無窮要比其他無窮大得多。實數集的“基數”也比自然數更大，因為實數更多。任何可數的集合要么是有窮的，要么如果是無窮的，且基數為 aleph-zero。

那么，數學家可以圍繞這些概念來做怎樣的研究？Friedman與Stanley 的論文，以及 Paolini 和 Shelah 的新工作都重點關注結構之間的同構（isomorphism）。雖然一些數學結構在本質上都是無窮，但仍有可能研究它們，并將它們與其他對象進行比較，以確定它們是否同構或大致相等。

例如，我們先看看兩個無窮但可數的數字組：

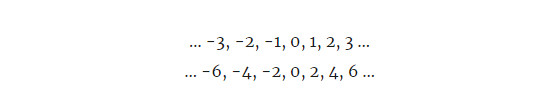
第一組由所有整數組成，第二組則僅由偶數組成。這兩個群彼此同構，因為它們具有相同數量的元素，也就是說，它們的無窮是相同的。而且，在這兩組里，每一組中的元素都能對應另一組中的一個元素。此外，用于從一組映射到另一組的函數還必須保留組的運算和屬性（如加法組合律）。

這類同構群并不完全相同，因為它們沒有相同的元素，但它們確實有平行結構：一組中的每個元素都與另一組中的單個元素直接相關。通過一個函數就可以將第一個結構轉換為第二個結構，如上例所示，只需將第一個結構中的每個元素乘以 2，就能得到第二個結構。如 Paolini 所介紹，即便沒有完全相同的內容，同構結構也有“相同形狀”。

同構概念正是 TFAB 問題的核心。

2

多復雜才算得上是復雜？

在 1989 年的論文中，Friedman 與 Stanley 主要想解決一個問題：給定一個可數結構族，既可以是無限組數字，也可以是圖，那么，確定該族的對象是否彼此同構有多難？

Friedman 與 Stanley舉了一個例子：有一組圖，每個圖都有可數但無窮個頂點。在兩個標記為“同構”的可數圖上，一個圖中的頂點與另一個圖中的頂點之間必須存在一對一的對應關系。如果一個圖中的兩個頂點由一條邊連接，那么另一個圖中相應的頂點也必須由一條邊連接。大約如下：

[[416189]]

Friedman 與 Stanley 提出，要確定兩個可數圖是否同構是極其復雜的。這使得所有可數圖家族都變成“波萊爾完備”（Borel complete）——這個表達由他們在1989年的論文中首創，因為他們借助了法國數學家 Émile Borel 所設計的波萊爾函數（Borel function）。

Friedman  與 Stanley 很好奇：“還有哪些可數對象是波萊爾完備的？”這個問題，也是描述集合論的核心主題之一。

從之后的幾年里，Friedman、Stanley和其他學者已經確定了幾類滿足波萊爾完備性標準的數學對象，包括樹（一種簡化的圖）、線性階數和數字集（自然或實數），字面上是順序排列，就像數軸上的數字一樣。

但在 1989 年論文所考慮的許多情況中，只有 TFAB 拒絕通過同構進行分類。首先，TFAB群在本質上是一組數字。每個 TFAB 由遵循特定群規則的實數的可數子集組成，例如在加減規則下封閉（因此對于該群中的任何數字 p 和 q，p + q 和 p - q 也包含在群中）。它還遵守交換律（即 p + q = q + p），這也是阿貝爾群的標志。最后，“無撓”（torsion-free）的意思是，如果 g 是群中的非零元素，那么 g + g 永遠不可能等于零，g + g + g 也不能，g + g + g +g 也不能……依此類推。

30多年來，數學家們一直想知道：“如果我們有兩個（可數）無撓阿貝爾群，那么，當我們在詢問它們是否同構時，這個問題的難度是簡單、中等還是最難？”在1989年論文所提出的問題中，這個問題所用的解決時間最長。

終于，在今年，Shelah 和 Paolini 找到了突破的方法。

3

跨結構轉換

他們解決這個問題的方法，是借鑒了經典數學家思維：將一個難題簡化為一個容易的問題。如果他們能夠證明 TFAB 與另一個已知的波萊爾完備結構族（例如可數圖族）一樣復雜，那么也就可以證明 TFAB 也是波萊爾完備的。

這就好比，如果你想知道一個人是否是世界上最高的人，那么與其將Ta和地球上的每個人都比對，還不如去找被公認為最高的人比，看看誰更高。

Shelah 解釋，在決定使用可數圖作為衡量標準后，他們面臨關鍵的下一步：創建一個函數（特別是波萊爾類的函數），可以“將一個圖轉換成一個無撓阿貝爾群”。他們的函數需要接收一個圖作為輸入，并產生一個 TFAB 作為輸出，在這個過程中將信息從圖傳遞到 TFAB 群。也就是說，函數 f 必須滿足以下關系：當且僅當 f(G) 和 f(H) 是可數且彼此同構的 TFAB 時，兩個可數圖 G 和 H 才彼此同構。

這項任務并不容易，因為沒有“技術”來連接如此不同的數學對象。所以，他們不得不為這個問題發明一項“技術”。

用 Laskowski 的說法，問題的關鍵是找出這項技術。就像蘋果與橙子，圖和群沒有相同的詞匯。在這種情況下，我們要做的就是建立對應關系。

然后，他們真的是在比較無窮組的蘋果和無窮組的橙子。幸運的是，他們找到了一種將問題簡化的方法：你只要處理一個通用的圖，而無需處理所有圖。這個通用圖非常龐大，以至于它的子圖已經包含了所有可能的可數圖。

通過這種方式，Paolini 和 Shelah 可以構建必要的函數，從而證明圖和 TFAB 處于一種平等的地位。他們找到了一種將無撓阿貝爾群與圖相關聯的方法，以便保留同構。

而且，由于數學家已經知道可數圖族是波萊爾完備的，也就是在同構方面是最復雜的，那么，也就是說，可數 TFAB 族也必須是波萊爾完備的。

4

研究前景

那么，他們的研究成果有可能取得更通用的結論嗎？Kechris 的說法是：有待觀察，但很有可能。

在解決了可數 TFAB 的問題后，Paolini 和 Shelah 已經在進行進一步的探索，將研究目標對準不可數 TFAB，并稱“可能會有不一樣的結果”。

事實上，Shelah 有一個理論，就是當你將問題推到更高的基數時，問題可能會變得更簡單，因為當數字變得非常大時，重要數字之間的距離也會增加，比如質數和整數的平方。

同時，他們這篇關于可數 TFAB 的論文已經有一些直接的實際意義。例如，這個族沒有能夠告訴你兩個 TFAB 是否同構的鮮明屬性（即“不變量”），但可數 TFAB 的波萊爾完備性可以直接告訴你這個答案。

在未來，數學家們可能會發現其他類別的無窮可數結構，例如圖與 TFAB，它們在確定同構時最為復雜。不過，僅僅知道 TFAB 的可能復雜程度，就可以將問題進行簡化，都有利于幫助分類學家與描述集合理論家的進一步工作。