某團技術拷問:LinkedList 源碼看過嗎?
一、LinkedList 的剖白
大家好,我是 LinkedList,和 ArrayList 是同門師兄弟,但我倆練的內功卻完全不同。師兄練的是動態數組,我練的是鏈表。
問大家一個問題,知道我為什么要練鏈表這門內功嗎?
舉個例子來講吧,假如你們手頭要管理一推票據,可能有一張,也可能有一億張。
該怎么辦呢?
申請一個 10G 的大數組等著?那萬一票據只有 100 張呢?
申請一個默認大小的數組,隨著數據量的增大擴容?要知道擴容是需要重新復制數組的,很耗時間。
關鍵是,數組還有一個弊端就是,假如現在有 500 萬張票據,現在要從中間刪除一個票據,就需要把 250 萬張票據往前移動一格。
遇到這種情況的時候,我師兄幾乎情緒崩潰,難受的要命。師父不忍心看到師兄這樣痛苦,于是打我進入師門那一天,就強迫我練鏈表這門內功,一開始我很不理解,害怕師父偏心,不把師門最厲害的內功教我。
直到有一天,我親眼目睹師兄差點因為移動數據而走火入魔,我才明白師父的良苦用心。從此以后,我苦練“鏈表”這門內功,取得了顯著的進步,師父和師兄都夸我有天賦。
鏈表這門內功大致分為三個層次:
- 第一層叫做“單向鏈表”,我只有一個后指針,指向下一個數據;
- 第二層叫做“雙向鏈表”,我有兩個指針,后指針指向下一個數據,前指針指向上一個數據。
- 第三層叫做“二叉樹”,把后指針去掉,換成左右指針。
但我現在的功力還達不到第三層,不過師父說我有這個潛力,練成神功是早晚的事。
二、LinkedList 的內功心法
好了,經過我這么樣的一個剖白后,大家對我應該已經不陌生了。那么接下來,我給大家展示一下我的內功心法。
我的內功心法主要是一個私有的靜態內部類,叫 Node,也就是節點。
- private static class Node<E> {
- E item;
- Node<E> next;
- Node<E> prev;
- Node(Node<E> prev, E element, Node<E> next) {
- this.item = element;
- this.next = next;
- this.prev = prev;
- }
- }
它由三部分組成:
- 節點上的元素
- 下一個節點
- 上一個節點
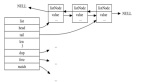
我畫幅圖給你們展示下吧。
- 對于第一個節點來說,prev 為 null;
- 對于最后一個節點來說,next 為 null;
- 其余的節點呢,prev 指向前一個,next 指向后一個。
我的內功心法就這么簡單,其實我早已經牢記在心了。但師父叮囑我,每天早上醒來的時候,每天晚上睡覺的時候,一定要默默地背誦一遍。雖然我有些厭煩,但我對師父的教誨從來都是言聽計從。
三、LinkedList 的招式
和師兄 ArrayList 一樣,我的招式也無外乎“增刪改查”這 4 種。在此之前,我們都必須得初始化。
- LinkedList<String> list = new LinkedList();
師兄在初始化的時候,默認大小為 10,也可以指定大小,依據要存儲的元素數量來。我就不需要。
1)招式一:增
可以調用 add 方法添加元素:
- list.add("沉默王二");
- list.add("沉默王三");
- list.add("沉默王四");
add 方法內部其實調用的是 linkLast 方法:
- public boolean add(E e) {
- linkLast(e);
- return true;
- }
linkLast,顧名思義,就是在鏈表的尾部鏈接:
- void linkLast(E e) {
- final Node<E> l = last;
- final Node<E> newNode = new Node<>(l, e, null);
- last = newNode;
- if (l == null)
- first = newNode;
- else
- l.next = newNode;
- size++;
- modCount++;
- }
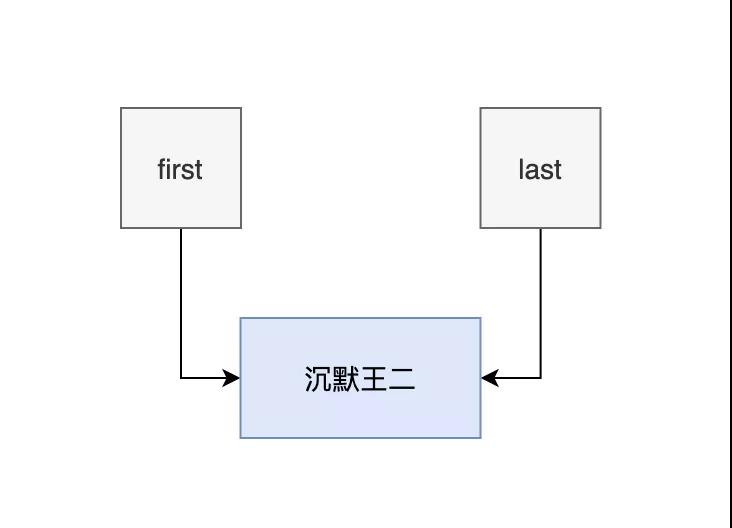
- 添加第一個元素的時候,first 和 last 都為 null。
- 然后新建一個節點 newNode,它的 prev 和 next 也為 null。
- 然后把 last 和 first 都賦值為 newNode。
此時還不能稱之為鏈表,因為前后節點都是斷裂的。
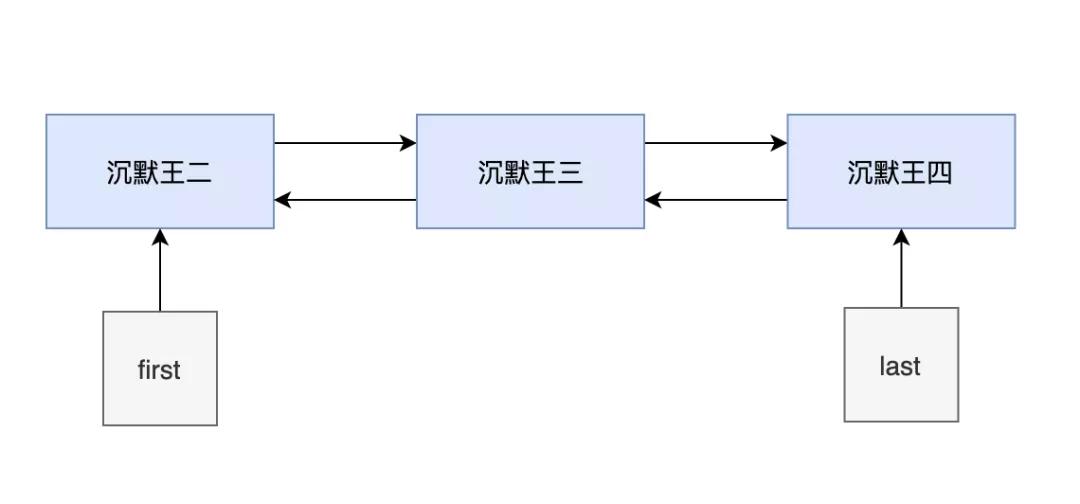
- 添加第二個元素的時候,first 和 last 都指向的是第一個節點。
- 然后新建一個節點 newNode,它的 prev 指向的是第一個節點,next 為 null。
- 然后把第一個節點的 next 賦值為 newNode。
此時的鏈表還不完整。
- 添加第三個元素的時候,first 指向的是第一個節點,last 指向的是最后一個節點。
- 然后新建一個節點 newNode,它的 prev 指向的是第二個節點,next 為 null。
- 然后把第二個節點的 next 賦值為 newNode。
此時的鏈表已經完整了。
我這個增的招式,還可以演化成另外兩個:
- addFirst() 方法將元素添加到第一位;
- addLast() 方法將元素添加到末尾。
addFirst 內部其實調用的是 linkFirst:
- public void addFirst(E e) {
- linkFirst(e);
- }
linkFirst 負責把新的節點設為 first,并將新的 first 的 next 更新為之前的 first。
- private void linkFirst(E e) {
- final Node<E> f = first;
- final Node<E> newNode = new Node<>(null, e, f);
- first = newNode;
- if (f == null)
- last = newNode;
- else
- f.prev = newNode;
- size++;
- modCount++;
- }
addLast 的內核其實和 addFirst 差不多,就交給大家自行理解了。
2)招式二:刪
我這個刪的招式還挺多的:
- remove():刪除第一個節點
- remove(int):刪除指定位置的節點
- remove(Object):刪除指定元素的節點
- removeFirst():刪除第一個節點
- removeLast():刪除最后一個節點
remove 內部調用的是 removeFirst,所以這兩個招式的功效一樣。
remove(int) 內部其實調用的是 unlink 方法。
- public E remove(int index) {
- checkElementIndex(index);
- return unlink(node(index));
- }
unlink 方法其實很好理解,就是更新當前節點的 next 和 prev,然后把當前節點上的元素設為 null。
- E unlink(Node<E> x) {
- // assert x != null;
- final E element = x.item;
- final Node<E> next = x.next;
- final Node<E> prev = x.prev;
- if (prev == null) {
- first = next;
- } else {
- prev.next = next;
- x.prev = null;
- }
- if (next == null) {
- last = prev;
- } else {
- next.prev = prev;
- x.next = null;
- }
- x.item = null;
- size--;
- modCount++;
- return element;
- }
remove(Object) 內部也調用了 unlink 方法,只不過在此之前要先找到元素所在的節點:
- public boolean remove(Object o) {
- if (o == null) {
- for (Node<E> x = first; x != null; x = x.next) {
- if (x.item == null) {
- unlink(x);
- return true;
- }
- }
- } else {
- for (Node<E> x = first; x != null; x = x.next) {
- if (o.equals(x.item)) {
- unlink(x);
- return true;
- }
- }
- }
- return false;
- }
這內部就分為兩種,一種是元素為 null 的時候,必須使用 == 來判斷;一種是元素為非 null 的時候,要使用 equals 來判斷。equals 是不能用來判 null 的,會拋出 NPE 錯誤。
removeFirst 內部調用的是 unlinkFirst 方法:
- public E removeFirst() {
- final Node<E> f = first;
- if (f == null)
- throw new NoSuchElementException();
- return unlinkFirst(f);
- }
unlinkFirst 負責的就是把第一個節點毀尸滅跡,并且捎帶把后一個節點的 prev 設為 null。
- private E unlinkFirst(Node<E> f) {
- // assert f == first && f != null;
- final E element = f.item;
- final Node<E> next = f.next;
- f.item = null;
- f.next = null; // help GC
- first = next;
- if (next == null)
- last = null;
- else
- next.prev = null;
- size--;
- modCount++;
- return element;
- }
3)招式三:改
可以調用 set() 方法來更新元素:
- list.set(0, "沉默王五");
來看一下 set() 方法:
- public E set(int index, E element) {
- checkElementIndex(index);
- Node<E> x = node(index);
- E oldVal = x.item;
- x.item = element;
- return oldVal;
- }
首先對指定的下標進行檢查,看是否越界;然后根據下標查找原有的節點:
- Node<E> node(int index) {
- // assert isElementIndex(index);
- if (index < (size >> 1)) {
- Node<E> x = first;
- for (int i = 0; i < index; i++)
- x = x.next;
- return x;
- } else {
- Node<E> x = last;
- for (int i = size - 1; i > index; i--)
- x = x.prev;
- return x;
- }
- }
size >> 1:也就是右移一位,相當于除以 2。對于計算機來說,移位比除法運算效率更高,因為數據在計算機內部都是二進制存儲的。
換句話說,node 方法會對下標進行一個初步判斷,如果靠近前半截,就從下標 0 開始遍歷;如果靠近后半截,就從末尾開始遍歷。
找到指定下標的節點就簡單了,直接把原有節點的元素替換成新的節點就 OK 了,prev 和 next 都不用改動。
4)招式四:查
我這個查的招式可以分為兩種:
- indexOf(Object):查找某個元素所在的位置
- get(int):查找某個位置上的元素
indexOf 的內部分為兩種,一種是元素為 null 的時候,必須使用 == 來判斷;一種是元素為非 null 的時候,要使用 equals 來判斷。因為 equals 是不能用來判 null 的,會拋出 NPE 錯誤。
- public int indexOf(Object o) {
- int index = 0;
- if (o == null) {
- for (Node<E> x = first; x != null; x = x.next) {
- if (x.item == null)
- return index;
- index++;
- }
- } else {
- for (Node<E> x = first; x != null; x = x.next) {
- if (o.equals(x.item))
- return index;
- index++;
- }
- }
- return -1;
- }
get 方法的內核其實還是 node 方法,這個之前已經說明過了,這里略過。
- public E get(int index) {
- checkElementIndex(index);
- return node(index).item;
- }
其實,查這個招式還可以演化為其他的一些,比如說:
- getFirst() 方法用于獲取第一個元素;
- getLast() 方法用于獲取最后一個元素;
- poll() 和 pollFirst() 方法用于刪除并返回第一個元素(兩個方法盡管名字不同,但方法體是完全相同的);
- pollLast() 方法用于刪除并返回最后一個元素;
- peekFirst() 方法用于返回但不刪除第一個元素。
四、LinkedList 的挑戰
說句實在話,我不是很喜歡和師兄 ArrayList 拿來比較,因為我們各自修煉的內功不同,沒有孰高孰低。
雖然師兄經常喊我一聲師弟,但我們之間其實挺和諧的。但我知道,在外人眼里,同門師兄弟,總要一較高下的。
比如說,我們倆在增刪改查時候的時間復雜度。
也許這就是命運吧,從我進入師門的那天起,這種爭論就一直沒有停息過。
無論外人怎么看待我們,在我眼里,師兄永遠都是一哥,我敬重他,他也愿意保護我。
好了,LinkedList 這篇就到這了。
本文轉載自微信公眾號「沉默王二」,可以通過以下二維碼關注。轉載本文請聯系沉默王二公眾號。